どちらに曲がるのか
電場領域
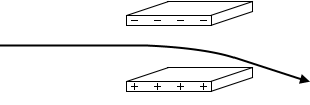 等速直線運動をする”負”に帯電した荷電粒子に上向きの電場を掛ければ、下向きに運動方向が変わります。
このように荷電粒子の向きを変えるための電極を偏向電極といいます。
等速直線運動をする”負”に帯電した荷電粒子に上向きの電場を掛ければ、下向きに運動方向が変わります。
このように荷電粒子の向きを変えるための電極を偏向電極といいます。
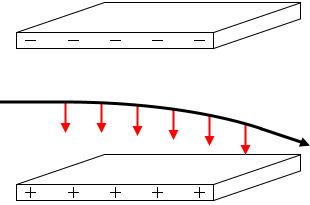 電場の掛かった領域を進行中は常に下向きの静電気力(クーロン力)を受けます。つまり、この運動の軌道は水平投射と同じ放物線になります。
電場の掛かった領域を進行中は常に下向きの静電気力(クーロン力)を受けます。つまり、この運動の軌道は水平投射と同じ放物線になります。
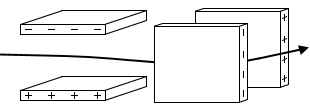
2方向から電場を掛けると荷電粒子の飛ぶ方向を
上下左右、自在に変えることができます。
昔のテレビに使われていたブラウン管の原理です。
磁場領域
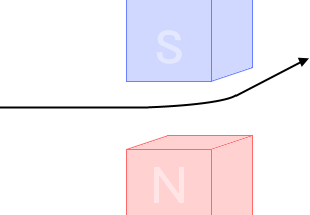 左図のように右向きに等速直線運動をする負に帯電した荷電粒子に上向きの磁場を掛ければ、紙面向こう側へ運動方向は変わります。
このとき使われる磁石を偏向磁石といいます。
左図のように右向きに等速直線運動をする負に帯電した荷電粒子に上向きの磁場を掛ければ、紙面向こう側へ運動方向は変わります。
このとき使われる磁石を偏向磁石といいます。
磁石ではなくコイルを使った場合には偏向コイルといいます。
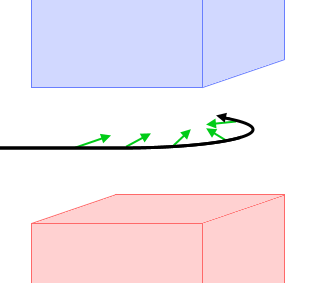 磁場の掛かった領域を進行中はローレンツ力を受け、フレミングの左手の法則により磁場に垂直の方向に曲げられ、その軌道は円になります。(トムソンの実験においては磁場領域は狭く、”円”を描く前に領域外へ飛び出していきます
磁場の掛かった領域を進行中はローレンツ力を受け、フレミングの左手の法則により磁場に垂直の方向に曲げられ、その軌道は円になります。(トムソンの実験においては磁場領域は狭く、”円”を描く前に領域外へ飛び出していきます
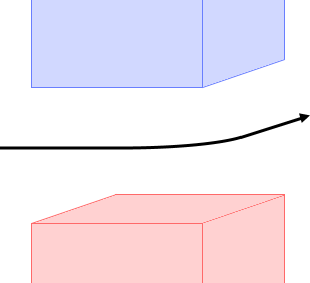 )
)
トムソンの実験
陰極線の正体が負の荷電粒子(電子)ではないかと考えたJ.J. トムソン
1856年–1940年のイギリスの物理学者、ジョゼフ⋅ジョン⋅トムソン。陰極線に電場を掛けると進行方向が曲がることを発見し、陰極線の正体が電荷を持った粒子であることを証明しました。電子の発見者とされています。また、原子模型としてブドウパンモデルを提唱しました。
は、以下のような装置を作って、その荷電粒子の比電荷を調べました。
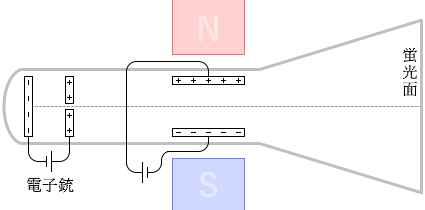 減圧されたガラス管内で、電子銃から発射された電子の進路を、電極によって、あるいは磁石によって曲げ
実際には磁石ではなくコイルを使うことが多いです。
減圧されたガラス管内で、電子銃から発射された電子の進路を、電極によって、あるいは磁石によって曲げ
実際には磁石ではなくコイルを使うことが多いです。
上の*の中で説明した偏向コイルです。
、蛍光面のどこに当たるかを測定します。
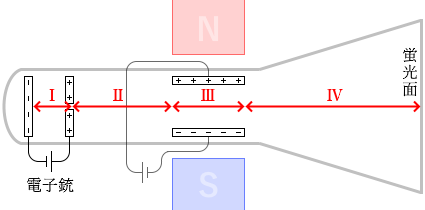 電子は領域Ⅰ(電子銃の領域)で加速し、領域Ⅱで等速直線運動をし、領域Ⅲ(電場領域、磁場領域)で方向を曲げられ、領域Ⅳで等速直線運動をし、蛍光面に到達します。
電子は領域Ⅰ(電子銃の領域)で加速し、領域Ⅱで等速直線運動をし、領域Ⅲ(電場領域、磁場領域)で方向を曲げられ、領域Ⅳで等速直線運動をし、蛍光面に到達します。
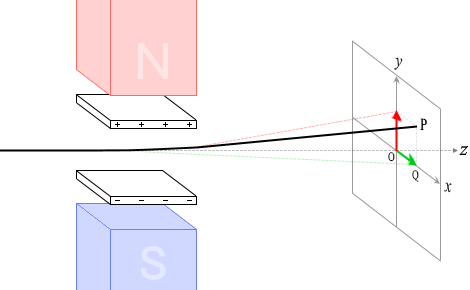 領域Ⅲに入る直前の電子の進路を \(z\)軸とし、電極によって曲げられる↑方向の軸を \(y\)軸、磁石によって曲げられる→方向の軸を \(x\)軸とします。
領域Ⅲに入る直前の電子の進路を \(z\)軸とし、電極によって曲げられる↑方向の軸を \(y\)軸、磁石によって曲げられる→方向の軸を \(x\)軸とします。
電子は電場、磁場以外に重力によっても曲げられるはずですが、電子の速さに対してガラス管の長さが短いので、その影響は極めて小さく、無視することにします。電場、磁場に比べて重力の影響は極めて小さいということです。
電場による偏向
まず、磁場のことは置いておいて、電場による偏向について考えてみます。各量を下記のように定めます。
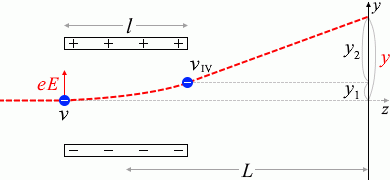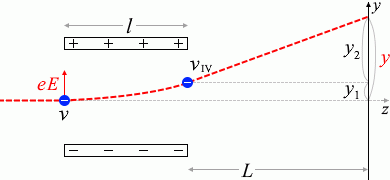
\(L\) の左端に関しては、電極の真ん中と定めても、電極の端と定めてもどちらでも構いません。
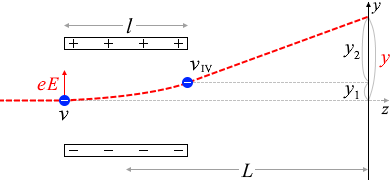 電子の質量を \(m\) [kg]、電気量を -\(e\) [C] とし、領域Ⅲに入射する直前の速度を \(v\) [m/s]、電場の強さを \(E\) [V/m]
もし、電極間の電圧を \(V\) [V] 、電極間の距離を \(d\) [m] とでもすれば、電場の強さは \({\large\frac{V}{d}}\) [V/m] です。
電子の質量を \(m\) [kg]、電気量を -\(e\) [C] とし、領域Ⅲに入射する直前の速度を \(v\) [m/s]、電場の強さを \(E\) [V/m]
もし、電極間の電圧を \(V\) [V] 、電極間の距離を \(d\) [m] とでもすれば、電場の強さは \({\large\frac{V}{d}}\) [V/m] です。
あと、[V/m] は [N/C] でもあります。
とします。
入射した電子は下向きの電場によって上向きに \(eE\) [N] の静電気力を受けます
\(\vec{F}\) = \(q\vec{E}\) の \(q\) の部分が今は \(e\) です。
。運動方程式(\(ma\) = \(F\) の式)を立てますと、加速度 \(a\) [m/s2] は、
\(ma\) = \(eE\)
∴ \(a\) = \({\large\frac{eE}{m}}\)
電子の運動のうち \(y\)軸方向成分はこの加速度で等加速度直線運動
初速 0 の等加速度直線運動
\(v\) = \(at\)
\(x\) = \({\large\frac{1}{2}}at^2\)
\(v^2 - 0^2\) = \(2ax\)
をするわけですが、\(z\)軸方向へは(力を受けないので)\(v\) [m/s] の速さで等速直線運動をします。
ここで、距離 \(l\) [m] の領域Ⅲを通過するのに掛かる時間を \(t_Ⅲ\) [s] と置くと、
\(t_Ⅲ\) = \({\large\frac{l}{v}}\)
であり、曲げられる幅 \(y_1\) [m] は
\(y_1\) = \({\large\frac{1}{2}}{at_Ⅲ}^2\) = \({\large\frac{1}{2}}⋅{\large\frac{eE}{m}}⋅\big({\large\frac{l}{v}}\big)^2\)
となります。
領域Ⅲから出るときの速さを \(v_Ⅳ\) [m/s] とすると、その \(y\)成分
初速 0 の等加速度直線運動
\(v\) = \(at\)
\(x\) = \({\large\frac{1}{2}}at^2\)
\(v^2 - 0^2\) = \(2ax\)
は
\(v_{Ⅳy}\) = \(at_Ⅲ\) = \({\large\frac{eE}{m}}⋅{\large\frac{l}{v}}\)
であり、\(z\)成分は \(v\) のままであり、距離 \(L - {\large\frac{l}{2}}\) [m] の領域Ⅳを通過するのに掛かる時間を \(t_Ⅳ\) と置くと、
\(t_Ⅳ\) = \({\large\frac{L-\frac{l}{2}}{v}}\)
であるので、領域Ⅳを通過する間に振れる幅 \(y_2\) [m] は
\(y_2\) = \(v_{Ⅳy} × t_Ⅳ\) = \({\large\frac{eE}{m}}⋅{\large\frac{l}{v}}⋅{\large\frac{L-\frac{l}{2}}{v}}\)
であり、\(y_1\) と \(y_2\) が求められたので足し合わせますと、
\(y\) = \(y_1 + y_2\)
= \({\large\frac{1}{2}}⋅{\large\frac{eE}{m}}⋅\big({\large\frac{l}{v}}\big)^2 + {\large\frac{eE}{m}}⋅{\large\frac{l}{v}}⋅{\large\frac{L-\frac{l}{2}}{v}}\)
= \({\large\frac{eE}{m}}⋅\Big\{{\large\frac{1}{2}}⋅\big({\large\frac{l}{v}}\big)^2 + {\large\frac{l}{v}}⋅{\large\frac{L-\frac{l}{2}}{v}}\Big\}\)
= \({\large\frac{eE}{m}}⋅\Big\{{\large\frac{1}{2}}⋅\big({\large\frac{l}{v}}\big)^2 + {\large\frac{l}{v}}⋅{\large\frac{L}{v}} - {\large\frac{1}{2}}⋅\big({\large\frac{l}{v}}\big)^2\)\(\Big\}\)
= \({\large\frac{eE}{m}}⋅\Big\{{\large\frac{l}{v}}⋅{\large\frac{L}{v}}\Big\}\)
= \({\large\frac{eE}{m}}⋅{\large\frac{lL}{v{^2}}}\)
変形しますと、
\({\large\frac{e}{m}}\) = \({\large\frac{v{^2}}{ElL}}y\) ……①
となり、比電荷の式が求められました。しかし右辺の各量のうち \(v\) は測定が困難です。あまりにも速すぎるので測定できません。というわけで、J.J. トムソンはさらに磁場を掛けて曲がり具合を測定しました。
磁場による偏向
電場のことは置いておいて、磁場による偏向について考えます。下図はガラス管を上から見た図です。
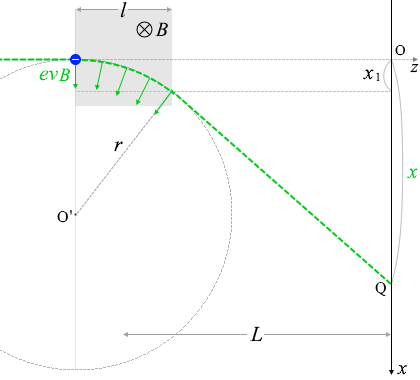 磁場の方向は、紙面向こう向きです。電子が \(z\)軸正の方向(右方向)へ向かっているので、電流の向きは \(z\)軸負の方向(左方向)です。フレミングの左手の法則を適用しますと、ローレンツ力の向きは上図の半径 \(r\) [m] の円の中心の方向です。
磁場の方向は、紙面向こう向きです。電子が \(z\)軸正の方向(右方向)へ向かっているので、電流の向きは \(z\)軸負の方向(左方向)です。フレミングの左手の法則を適用しますと、ローレンツ力の向きは上図の半径 \(r\) [m] の円の中心の方向です。
磁束密度を \(B\) [T] とすると、ローレンツ力の大きさは \(evB\) [N] であり、円運動の運動方程式を立てますと、
\(m{\large\frac{v{^2}}{r}}\) = \(evB\)
∴ \(m{\large\frac{v}{r}}\) = \(eB\)
∴ \({\large\frac{mv}{eB}}\) = \(r\) ……②
次に下図のように各点を定めます。
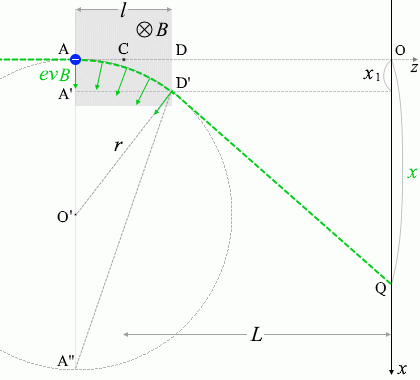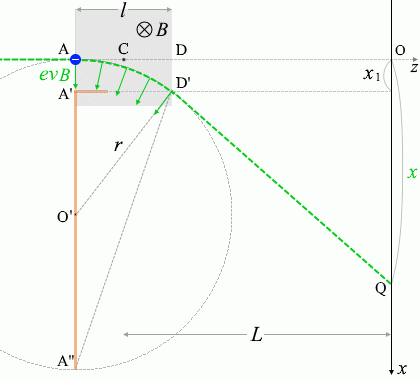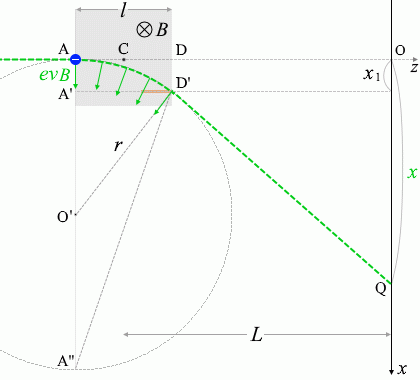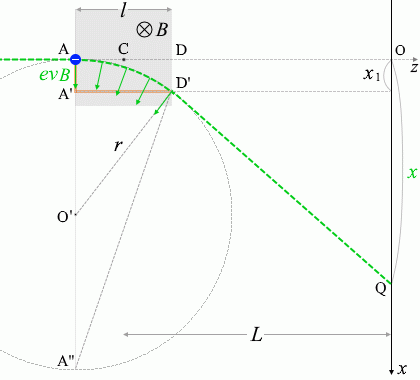 そうしますと、△D'A'Aと△A''A'D'は相似だから
相似になることはお分かりでしょうか。
そうしますと、△D'A'Aと△A''A'D'は相似だから
相似になることはお分かりでしょうか。
三角形の内角の和が180°であることと、
直径に対する円周角が直角であるというタレスの定理、
を思い出してください。
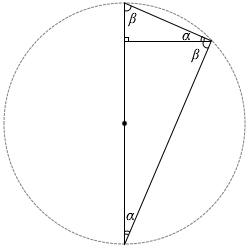
\(α + β\) = 90° となっています。
、
\({\large\frac{\rm{A'A}}{\rm{D'A'}}}\) = \({\large\frac{\rm{A'D'}}{\rm{A''A'}}}\)
A'A = \(x_1\) 、D'A' = \(l\) であり、
\(x_1\) ≪ \(r\) のとき A''A' ≒ A''A = \(2r\) であるので
実際には \(x_1\) はとても小さく、\(r\) はとても大きくなっています。
上式は
\({\large\frac{x_1}{l}}\) = \({\large\frac{l}{2r}}\)
∴ \(r\) = \({\large\frac{l^2}{2x_1}}\)
この式に②式を代入しますと、
\({\large\frac{mv}{eB}}\) = \({\large\frac{l^2}{2x_1}}\)
∴ \(x_1\) = \({\large\frac{eBl^2}{2mv}}\) ……③
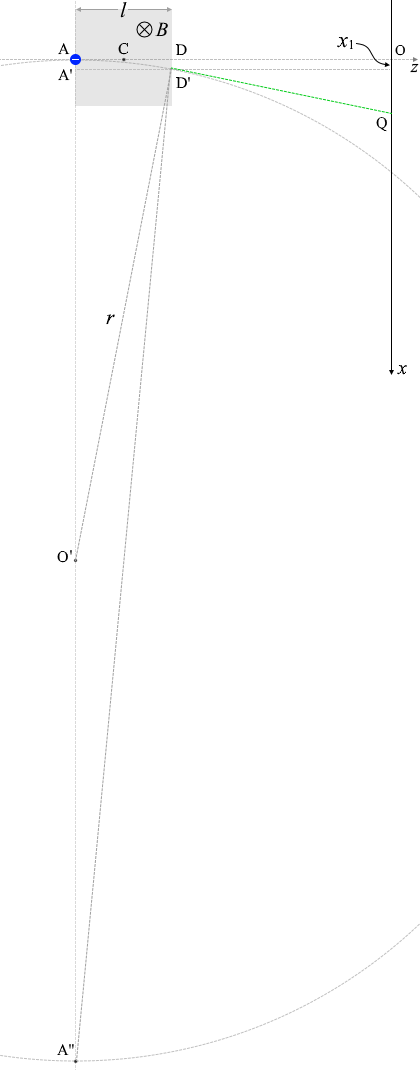
次に、\(x\) の大きさを求めます。
領域Ⅳでは等速直線運動をするわけですが、その軌跡QD'を延長すると、ADの中点C
円に接する接線2本によって作られる三角形は必ず二等辺三角形になります。
二等辺でない三角形は作れません。
よって、AC = CD' となります。
そして、△ADD'は実際にはとても細長い三角形です。

よって、CD' ≒ CD であり、AC ≒ CD となります。
つまり、点CはADの(ほぼ)中点です。
と交わります。
すると、△CDD'と△COQは相似になり、
\({\large\frac{\rm{DD'}}{\rm{CD}}}\) = \({\large\frac{\rm{OQ}}{\rm{CO}}}\)
DD' = \(x_1\) 、CD = \({\large\frac{l}{2}}\) 、OQ = \(x\) 、CO = \(L\) であるので上式は
\({\large\frac{x_1}{\frac{l}{2}}}\) = \({\large\frac{\color{#0c0}{x}}{L}}\)
∴ \({\large\frac{2x_1}{l}}\) = \({\large\frac{\color{#0c0}{x}}{L}}\)
∴ \(x\) = \({\large\frac{2L}{l}}x_1\)
この式に③式を代入しますと、
\(x\) = \({\large\frac{2L}{l}}⋅{\large\frac{eBl^2}{2mv}}\) = \({\large\frac{eBlL}{mv}}\)
変形しますと、
\({\large\frac{e}{m}}\) = \({\large\frac{v}{BlL}}x\) ……④
電場による偏向と磁場による偏向の結果を合わせる
①式、④式より、
\({\large\frac{v{^2}}{ElL}}y\) = \({\large\frac{v}{BlL}}x\)
∴ \({\large\frac{v}{ElL}}y\) = \({\large\frac{1}{BlL}}x\)
∴ \({\large\frac{v}{E}}y\) = \({\large\frac{1}{B}}x\)
∴ \(v\) = \({\large\frac{Ex}{By}}\) ……⑤
右辺の各量は測定できるので \(v\) の値が求められます。
これを①式あるいは④式に代入し直せば、比電荷 \({\large\frac{e}{m}}\) も求められます。たとえば④式に代入しますと、
\({\large\frac{e}{m}}\) = \({\large\frac{v}{BlL}}x\) = \({\large\frac{\frac{Ex}{By}}{BlL}}x\) = \({\large\frac{Ex}{B^2lLy}}x\) = \({\large\frac{Ex^2}{B^2lLy}}\)
①式に代入しても、
\({\large\frac{e}{m}}\) = \({\large\frac{v{^2}}{ElL}}y\) = \({\large\frac{(\frac{Ex}{By}){^2}}{ElL}}y\) = \({\large\frac{(Ex){^2}}{B^2ElLy^2}}y\) = \({\large\frac{Ex^2}{B^2lLy}}\)
電場と磁場を直交させて電子をまっすぐ飛ばす
 上の実験では電場と磁場の向きが平行でしたが、
上の実験では電場と磁場の向きが平行でしたが、
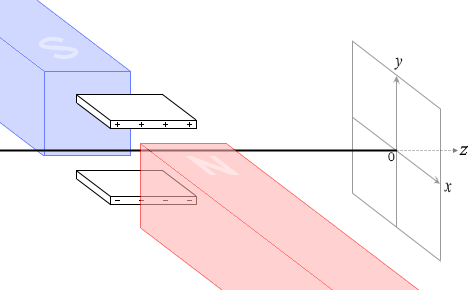 その向きを直交させて電子をまっすぐ飛ばしてみます。
その向きを直交させて電子をまっすぐ飛ばしてみます。
電場を下向き、磁場を紙面向こう向きに掛けて、その強さを調整し、電子がまっすぐ進むようにします。
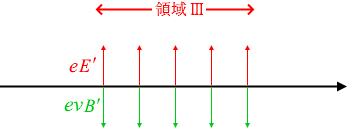
まっすぐ進むということは、電場による静電気力と磁場によるローレンツ力がつり合うということです
磁場によるローレンツ力は円を描くような方向にはたらくものですが、
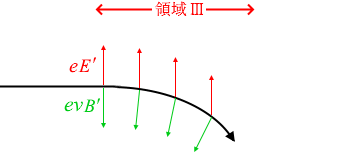
電子がまっすぐ進むということは、円弧を描かないということであり、静電気力とローレンツ力が常に反対向きでつり合っているということであり、つまりローレンツ力の向きは常に下向きということです。

微視的に見たらジグザグで、巨視的に見たら直線である、という感じにイメージしてもらってもいいです(不正確ですが)。
 。上で説明しましたが、電場の強さが \(E'\) [V/m] のときの静電気力は \(eE'\) [N] であり、磁束密度 \(B'\) [T] のときのローレンツ力は \(evB'\) [N] であるので、
。上で説明しましたが、電場の強さが \(E'\) [V/m] のときの静電気力は \(eE'\) [N] であり、磁束密度 \(B'\) [T] のときのローレンツ力は \(evB'\) [N] であるので、
\(eE'\) = \(evB'\)
∴ \(E'\) = \(vB'\)
∴ \(v\) = \({\large\frac{E'}{B'}}\)
このように、電子をまっすぐ飛ばすことによってその速度を割り出すことができます。
電子銃のエネルギー
その他に、電子銃の領域Ⅰにおけるエネルギーに着目して電子の速度 \(v\) と電子の比電荷 \({\large\frac{e}{m}}\) の関係を求める方法もあります。
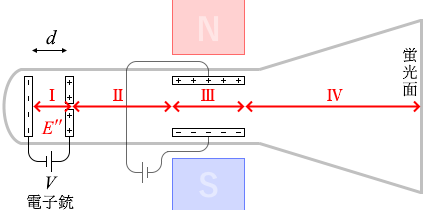
電子銃の電極間の電場の強さを \(E''\) [V/m] 、電極間の距離を \(d\) [m] 、電子銃に加える電圧を \(V\) [V] とします。電子はスタート地点の陰極(-極)では速度が 0 [m/s] で、すなわち運動エネルギーも 0 [J] で、\(E''\) の電場の中を \(d\) [m] 進んでいって陽極(+極)を通過する瞬間には速度が \(v\) [m/s] になっている
上の「電場による偏向」のところで「領域Ⅲに入射する直前の速度を \(v\) 」と定義しました。これは領域Ⅱにおける速度のことであり、領域Ⅱでは等速直線運動をするので、すなわち領域Ⅰを出る瞬間の速度は \(v\) ということであります。
ので運動エネルギーは \({\large\frac{1}{2}}mv^2\) [J] になっています。と同時に、陽極に存在する瞬間の位置エネルギー \(U\) [J] は \(U\) = \(eEd\) = \(eV\) になっています。(\(V\) を定義すれば \(E''\) や \(d\) は定義する必要は無かった…)
エネルギー保存の法則の式を立てますと、
\({\large\frac{1}{2}}mv^2 - {\large\frac{1}{2}}m⋅0^2\) = \(eV\)
∴ \({\large\frac{1}{2}}mv^2\) = \(eV\)
∴ \({\large\frac{1}{2}}v^2\) = \({\large\frac{e}{m}}V\)
∴ \({\large\frac{e}{m}}\) = \({\large\frac{v^2}{2V}}\)
この式の内、測定できる量は \(V\) だけで、\({\large\frac{e}{m}}\) や \(v\) の値は特定できないのですが、この式を④式 \({\large\frac{e}{m}}\) = \({\large\frac{v}{BlL}}x\) に代入すると、
\({\large\frac{v^2}{2V}}\) = \({\large\frac{v}{BlL}}x\)
∴ \({\large\frac{v}{2V}}\) = \({\large\frac{1}{BlL}}x\)
∴ \(v\) = \({\large\frac{2V}{BlL}}x\)
となり、右辺の各量は測定できるので左辺の \(v\) の値が特定できることになります。そして元の式に戻せば \({\large\frac{e}{m}}\) も特定できることになります。
また、④式でなく①式 \({\large\frac{e}{m}}\) = \({\large\frac{v{^2}}{ElL}}y\) に代入しようとすると、\({\large\frac{e}{m}}\) も \(v\) も消えてしまってうまくいきません。これはつまり、電子の比電荷、速度を特定するには、電場だけでは(もちろん磁場だけでも)うまくいかず、両方を用いなければならないということを意味しています。
 等速直線運動をする”負”に帯電した荷電粒子に上向きの
等速直線運動をする”負”に帯電した荷電粒子に上向きの 電場の掛かった領域を進行中は常に下向きの静電気力(クーロン力)を受けます。つまり、この運動の軌道は
電場の掛かった領域を進行中は常に下向きの静電気力(クーロン力)を受けます。つまり、この運動の軌道は
 左図のように右向きに等速直線運動をする負に帯電した荷電粒子に上向きの磁場を掛ければ、紙面向こう側へ運動方向は変わります。
左図のように右向きに等速直線運動をする負に帯電した荷電粒子に上向きの磁場を掛ければ、紙面向こう側へ運動方向は変わります。 磁場の掛かった領域を進行中は
磁場の掛かった領域を進行中は
 減圧されたガラス管内で、電子銃から発射された電子の進路を、電極によって、あるいは磁石によって曲げ
減圧されたガラス管内で、電子銃から発射された電子の進路を、電極によって、あるいは磁石によって曲げ 電子は領域Ⅰ(電子銃の領域)で加速し、領域Ⅱで等速直線運動をし、領域Ⅲ(電場領域、磁場領域)で方向を曲げられ、領域Ⅳで等速直線運動をし、蛍光面に到達します。
電子は領域Ⅰ(電子銃の領域)で加速し、領域Ⅱで等速直線運動をし、領域Ⅲ(電場領域、磁場領域)で方向を曲げられ、領域Ⅳで等速直線運動をし、蛍光面に到達します。 領域Ⅲに入る直前の電子の進路を \(z\)軸とし、電極によって曲げられる
領域Ⅲに入る直前の電子の進路を \(z\)軸とし、電極によって曲げられる
 電子の質量を \(m\) [kg]、電気量を -\(e\) [C] とし、領域Ⅲに入射する直前の速度を \(v\) [m/s]、電場の強さを \(E\) [V/m]
電子の質量を \(m\) [kg]、電気量を -\(e\) [C] とし、領域Ⅲに入射する直前の速度を \(v\) [m/s]、電場の強さを \(E\) [V/m]  磁場の方向は、紙面
磁場の方向は、紙面 そうしますと、△D'A'Aと△A''A'D'は相似だから
そうしますと、△D'A'Aと△A''A'D'は相似だから



 その向きを直交させて電子をまっすぐ飛ばしてみます。
その向きを直交させて電子をまっすぐ飛ばしてみます。


