光電効果
光電効果とは
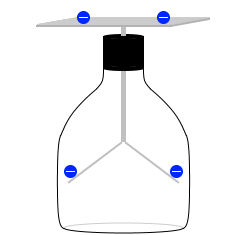 箔検電器の上にアルミ板または亜鉛板を載せ
アルミニウムや亜鉛は仕事関数(下で説明)が小さく、
箔検電器の上にアルミ板または亜鉛板を載せ
アルミニウムや亜鉛は仕事関数(下で説明)が小さく、
光電効果が起こりやすいです。
鉄や銅でも光電効果は起こりますが仕事関数が大きいので
光電効果を起こすのはちょっと大変です。
、全体を負に帯電させます。すると箔が開きますが、
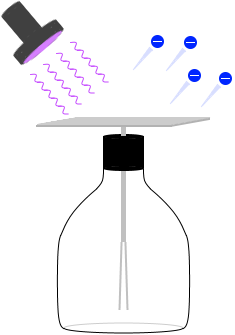 そこに紫外線を当てると箔が閉じます。負電荷が減ったのです。減ったのは上部の金属板から負電荷の電子が飛び出したためです。
箔検電器を負ではなく正に帯電させたときは
そこに紫外線を当てると箔が閉じます。負電荷が減ったのです。減ったのは上部の金属板から負電荷の電子が飛び出したためです。
箔検電器を負ではなく正に帯電させたときは
紫外線を当ててもなかなか箔は変化しません。
充分大きい振動数の光をたっぷり当てれば変化するでしょうが、
その場合は箔は閉じるのではなく開きます。
正に帯電していたところをさらに正に帯電させるからです。
このように、光のエネルギーによって物質内から電子が飛び出す現象を光電効果といい、飛び出した電子を光電子
光電子といっても実体は単なる電子です。名称が変わっただけです。
熱エネルギーをもらって飛び出した場合は熱電子と呼んだりします。
といいます。光を受けて発電する太陽光発電や光を受けて情報を記録する撮影素子や光センサーは光電効果によって動作します。
光電効果の性質
光電効果の奇妙な性質
当てる光の振動数がある値より小さいと、いくら光が強く(=明るく=光量が多く)ても電子が飛び出しません。この値の振動数を限界振動数といいます。\(ν_0\) と表すことが多いです
\(ν_0\) ニューゼロ。
なぜ \(ν\) が用いられるかは分かりません。
光速に関わる振動数には \(f\) ではなく \(ν\) を用いることが多いです。
波長については \(λ\) を用いることが多いです。
光速の \(c\) と合わせて
\(c\) = \(ν\)\(λ\)
というのが波の基本式です。
波動分野では \(v\) = \(fλ\) であるところが、
原子分野では \(c\) = \(ν\)\(λ\) ということです。
\(c\) は量記号ではなく定数です。\(c\) = 299792458 m/s です。
ややこしいです。が、すぐ慣れると思います。
。また、このときの波長を限界波長といいます。\(λ_0\) と表すことが多いです。(光の速度は一定なので振動数が決まると自動的に波長も決まります)。そして逆に、当てる光の振動数が限界振動数より大きいと、いくら光が弱くてもすぐに電子が飛び出します。
上の方の*の中で説明した「箔検電器を負ではなく正に帯電させたときは紫外線を当ててもなかなか箔は変化しません。」と矛盾していると思われるかもしれませんが、さすがに金属が正に帯電している場合は電子を飛び出させるのは難しいはずです。ここで言いたいのは、正にも負にも帯電しておらず金属表面も磨かれていてニュートラルな状態になっている場合に、ちょっと光を当てただけで光電効果が起こる、という意味です。
この限界振動数は金属の種類によって決まります。小さい振動数で光電効果が起こる金属もあれば、大きい振動数でないと光電効果が起こらない金属もあります。
さらに、飛び出した光電子の運動エネルギーの最大値は、当てる光の振動数が大きいほど大きく、光の強さには無関係です。飛び出す光電子の個数は光の強さに比例するのですが、一つ一つの光電子のエネルギーは光の強さではなく光の振動数に依存します。
飛び出す光電子の個数に関しては、光の強さに比例し、光の振動数に無関係です(もちろん限界振動数を上回っている場合の話です)。
これらの奇妙な性質は光を波動としてとらえた場合には矛盾しているように感じますが、光を粒子とみなすとうまく説明することができます。光には波動的な性質だけでなく粒子的な性質もあるのです。
運動エネルギーの最大値に着目
光電効果によって光電子が飛び出すわけですが、飛び出すということはスピードを持っているということであり、スピードを持っているということは運動エネルギーを持っているということになります。
そして光電効果を語るときに「光電子の運動エネルギー」ではなくわざわざ「光電子の運動エネルギーの最大値」とするのは、様々な大きさの運動エネルギーを持った光電子の中で最大の運動エネルギーを持っているものに着目する必要があるからです。
金属内の電子は原子核に引っ張られていますが、光電効果が起こるときはそれを引き離すわけです。そのとき引き離しやすい位置にいる電子もいれば引き離しにくい位置にいる電子もいて、引き離しにくい電子を引き離すのには労力が必要で、その分エネルギーを使うことになり、光電子のスピードは落ちてしまいます。あるいはせっかく引き離したのにどこかにぶつかってスピードが落ちてしまう光電子もいるかもしれません。そのような最大ではない運動エネルギーを持つ光電子については、光が光電子の運動エネルギーにどのくらい影響を与えたのか分かりません。光の影響力が100%運動エネルギーに変換されたとみなせません。100%きれいに変換されたとみなせるのは、引き離しやすい位置にいて、どこにも当たらずに飛び出した光電子です。様々な運動エネルギーを持った光電子の中で最大の運動エネルギーを持った光電子です。
光電管による光電効果
光電管という装置を使って実験すると、光電効果の様々な性質を明らかにすることができます。
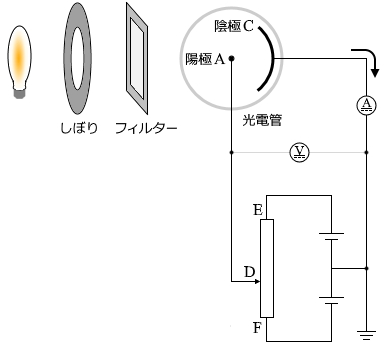 光電管とは陽極(正極)と陰極(負極)を内蔵した真空のガラス管で
陰極には亜鉛よりもっと仕事関数が小さくて光電効果を起こしやすい金属が用いられます。
光電管とは陽極(正極)と陰極(負極)を内蔵した真空のガラス管で
陰極には亜鉛よりもっと仕事関数が小さくて光電効果を起こしやすい金属が用いられます。
管内を真空にするのは、光電子が空気分子に当たらないようにするためです。金属表面を酸化させないためということもあるかもしれません。
、光が陰極に当たるとそこから電子が飛び出し、それが陽極に到達することによって回路に電流が流れます。このときの電流を光電流といいます
「こうでんりゅう」あるいは「ひかりでんりゅう」
光電流といっても実体は単なる電流です。
もちろん電流の向きは電子の移動方向と逆です。
。
水銀灯
水銀灯の光の色は白色に感じますが、いくつかの色が混じって白色に感じます。そのいくつかの色が(波長)577nmの黄緑、546nmの緑、435nmの青、405nmの紫、などとはっきりクッキリしていて、フィルターを通すと単色光をうまく抜き出すことができます。
から出た光はしぼりとフィルターを通って光電管の陰極に当たります。しぼりによって光の強さ(=明るさ=光量=光子の個数)を調整することができます。フィルターを交換することによって特定の振動数の光を抜き出すことができます。
陰極Cはアースされていて、電位は 0 です。また、電源の真ん中もアースされているので、接点Dが可変抵抗器の真ん中にあるときは陽極Aも電位が 0 です
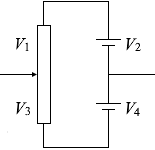
\(V_2\) = \(V_4\) のとき
\(V_1\) = \(V_3\) です。
\(V_2\) と \(V_4\) の真ん中の電位が 0 なら
\(V_1\) と \(V_3\) の真ん中の電位も 0 です。
。そして、接点DがE寄りにあるときは陽極Aの電位は正で、接点DがF寄りにあるときは陽極Aの電位は負です。
陽極、陰極のA、Cというのは anode アノード、cathode カソードの頭文字のつもりです。アルファベットの符号はなんでもいいです。
電源を用いるのは光電効果を起こすためではありません。電源が無くても光電効果は起こります。電源は陽極Aの電位(電圧)を変化させるためにあります。陰極に当てる光の強さ、光の振動数(フィルターの色)、陽極の電位、陰極の金属の種類、これらを変化させたときに光電流の大きさがどう変化するかを測定し、そこから光電効果の特徴を見出だす、というのがこの実験の目的です。
しぼりもフィルターも固定
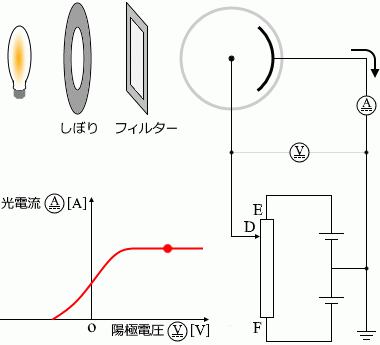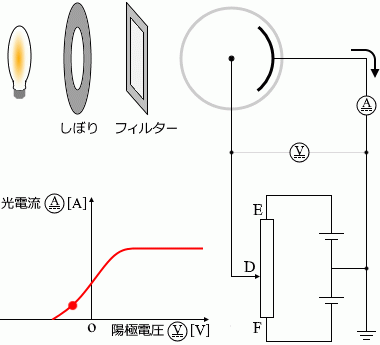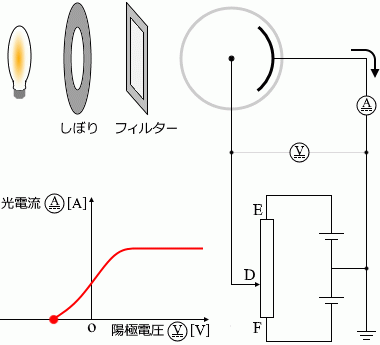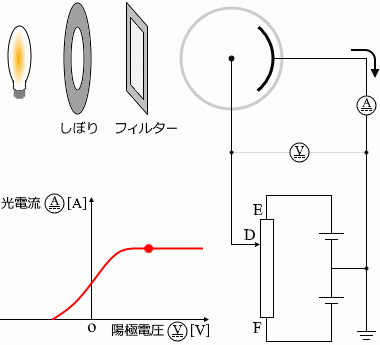 しぼりを固定し、フィルターも1種類に定めた上で、接点Dを動かすと電圧計と電流計の値は左のグラフのように変化します。電圧が 0 であっても電流は流れます。接点DをFに近づけていくと(陽極の電位を低くしていくと)ある時点で電流は流れなくなります
光電子が進行方向と逆向きの静電気力を受けるためです。
しぼりを固定し、フィルターも1種類に定めた上で、接点Dを動かすと電圧計と電流計の値は左のグラフのように変化します。電圧が 0 であっても電流は流れます。接点DをFに近づけていくと(陽極の電位を低くしていくと)ある時点で電流は流れなくなります
光電子が進行方向と逆向きの静電気力を受けるためです。
下の『光電管内の光電子の様子』をご参照ください。
。接点DをEに近づけていくと(陽極の電位を高くしていくと)ある時点で電流がそれ以上大きくならなくなります
光電子の進行方向と同じ向きの静電気力を受けるため光電流は大きくなっていきますが、光電効果の最大値に達してしまえばそれ以上電流は増えません。例えば、光子(下で説明)が 1秒間に100個、陰極に当たるなら、発生する光電子は最大で1秒間に100個です。陽極の電位をいくら高くしても最大で1秒間に100個です。
。
しぼりを変える
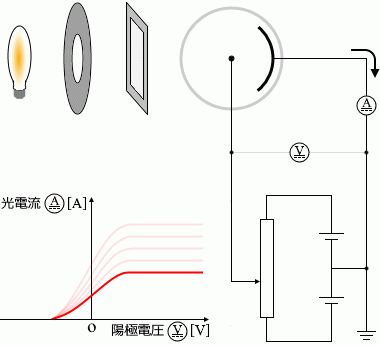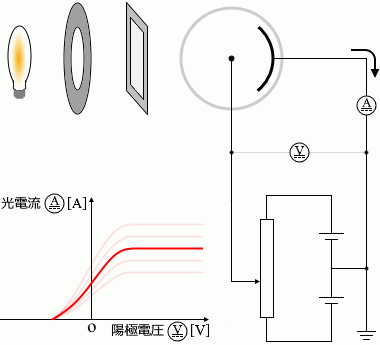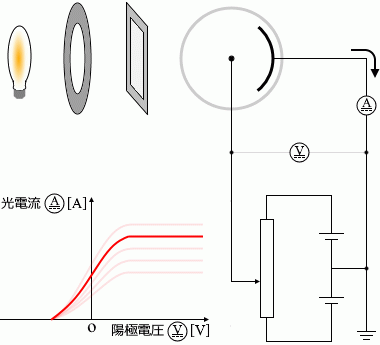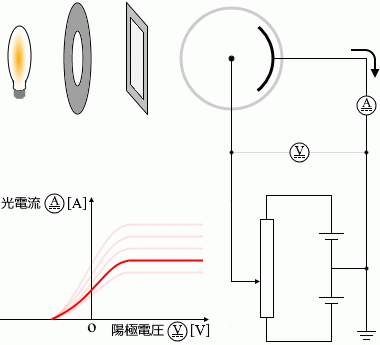 しぼりを拡げて光の強さを2倍にすると光電流も2倍になります
光の強さを2倍にするということは光子の個数を2倍にするということです。
しぼりを拡げて光の強さを2倍にすると光電流も2倍になります
光の強さを2倍にするということは光子の個数を2倍にするということです。
あと、光源が点光源であればその距離を変えることでしぼりの開け閉めと同じ効果を得ることができます。光の強さを2倍にしたければ距離を \({\large\frac{1}{\sqrt2}}\) にします。
。光電流が 0 になるときの電圧の値は変わりません。
フィルターを変える
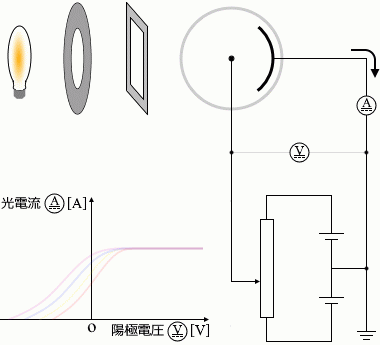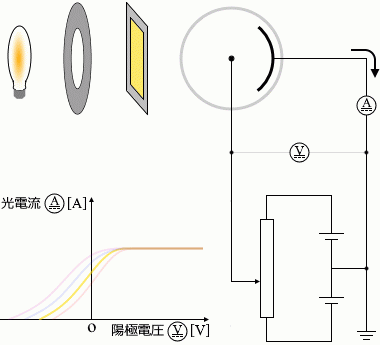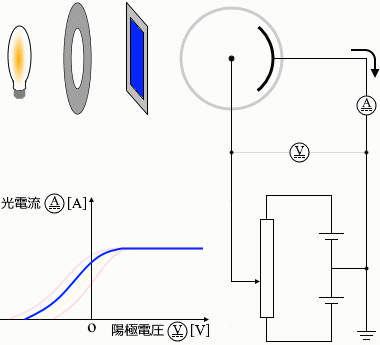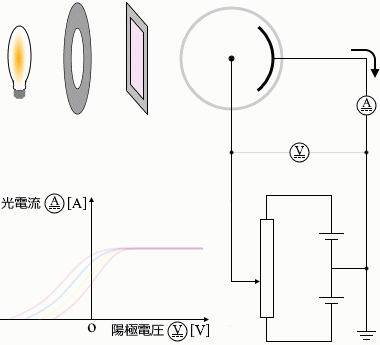 フィルターの色を赤→黄→青→紫と変えていくと
フィルターの色が赤色のときに光電効果が起こるような金属はあまりないです。セシウム Cs くらいでしょうか。
フィルターの色を赤→黄→青→紫と変えていくと
フィルターの色が赤色のときに光電効果が起こるような金属はあまりないです。セシウム Cs くらいでしょうか。
あと、フィルターを用いる代わりにプリズムを使って分光するという方法もあります。
光電流は大きくなります。最大値については(これは光の強さしだいなので)変わりません。光電流が 0 になるときの電圧の値は小さくなります(絶対値が大きくなる)。つまりグラフの曲線が左にズレたようになります。
陰極の金属の種類を変える
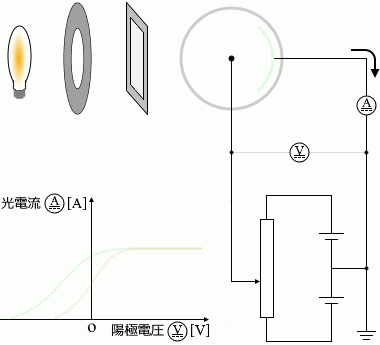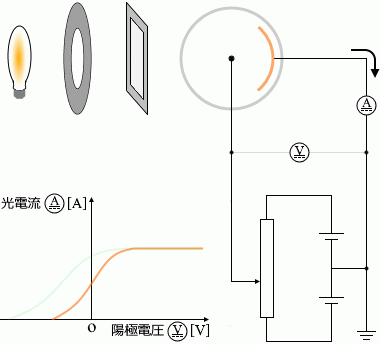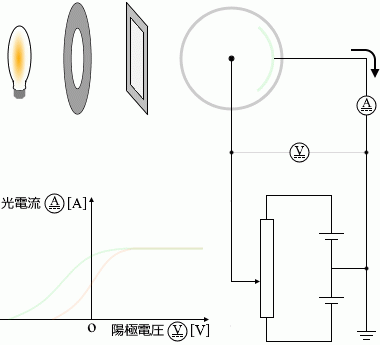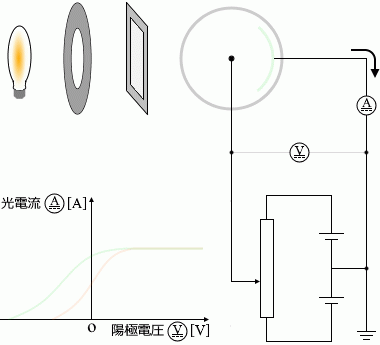 このことと同じように、陰極に用いる金属の種類を変えた場合も左図のように曲線が変化します。
このことと同じように、陰極に用いる金属の種類を変えた場合も左図のように曲線が変化します。
光電効果が起こりにくい、仕事関数(下で説明)が大きい金属のときは、左図のグラフのオレンジ色の曲線のように光電流は小さくなり、
光電効果が起こりやすい、仕事関数が小さい金属のときは、左図のグラフの緑色の曲線のように光電流は大きくなります。
光量子仮説
光量子仮説とは
光電効果の奇妙な性質を理論的に説明するのが光量子仮説です。
1900年にプランク
1858年–1947年のドイツの物理学者、マックス・プランク。
は、物質が振動数 \(ν\) の光を放射、吸収する場合、そのエネルギーは連続的でなく \(hν\) の整数倍の量となるという量子仮説を導き出しました。これは量子論、量子力学へとつながる画期的な発見でした。
連続的というのは 1.72859 だったり 3.9284 だったり 12.41982021 だったり 91.372 だったり自由な値をとるという意味で、そうではなく何らかの量の整数倍の値をとるということは最小の何らかの単位があるということであり、粒子的なものがあるということを示唆しています。電気素量のように。
量子とは物理量の最小単位という意味であり、量子的というのは連続的でないという意味であり、連続的な値をとると思われていたものがそうではなかったというのが量子論や量子力学です。
\(h\) はプランク定数と呼ばれ、その値は
\(h\) = 6.63 × 10-34 [J⋅s]
です
厳密な値は
\(h\) = 6.62607015 × 10-34 [J⋅s]
です。
\(h\) が何の頭文字であるかは分かりません。プランクが自身の論文の中で用いたようです。
あと完全に余談ですが、この定数には専用のフォントが用意されていて、「ℎ」と斜体となっています。ですのでこのフォントを使うならばhtmlにおいて <i>h</i> や <var>h</var> などとする必要はありません。
。単位は J⋅s ジュール秒 です
下で説明するように \(E\) = \(hν\) の関係があり、
単位の演算をしますと、
[J] = \(h\) × [Hz]
⇒ [J] = \(h\) × [1/s]
⇒ \(h\) = [J⋅s]
となります。
。この定数は物質の種類によりません。
その後、1905年にアインシュタイン
1879年–1955年のドイツの物理学者、アルベルト・アインシュタイン。
は、光は光子(フォトン)(あるいは光量子)という粒子が進行するもので、振動数 \(ν\) [Hz] の光の場合、光子1個のエネルギー \(E\) [J] は
\(E\) = \(hν\) [J]
であるというアインシュタインの光量子仮説(あるいは光量子説)を提唱しました。
光速を \(c\) [m/s] 、波長を \(λ\) [m] としますと、\(c\) = \(νλ\) の関係がありますからこれを上式に代入すると、
\(E\) = \({\large\frac{hc}{λ}}\) [J]
となります。
光が強いとか電磁波のエネルギーが大きいということは、波動としての観点からはその振幅が大きいということでしたが、粒子としての観点からはその個数が多いということになります。
光子1個のエネルギーの例
赤色の可視光線の波長は 700nm くらいですが、振動数を求めますと、
\(ν\) = \({\large\frac{c}{λ}}\) = \({\large\frac{3.00×10^8}{700×10^{−9}}}\) = \({\large\frac{3}{7}}\) × 1015
であり、これにプランク定数を掛けると、
\(E\) = \(hν\) = 6.63 × 10-34 × \({\large\frac{3}{7}}\) × 1015 ≒ 2.84 × 10-19
となり、つまり波長 700nm の赤色の光子1個のエネルギーは 2.84 × 10-19 [J] ということです。
波長がその半分の 350nm の紫外線であれば、光子1個のエネルギーは 5.68 × 10-19 [J] です。
(下で説明する電子ボルトという単位で表すと、それぞれ 1.60 × 10-19 で割って)
波長 700nm の光子1個のエネルギー:1.78 [eV]
波長 350nm の光子1個のエネルギー:3.55 [eV]
光量子仮説による光電効果の説明
光量子仮説では、\(hν\) [J] のエネルギーを持った1個の光子が金属表面の1個の電子に当たり、光子は消滅し、光子のエネルギーを得た電子が原子核からの引力を振りほどき、光電子となって金属の外へ飛び出る、と考えます。
このときもエネルギー保存の法則がはたらきます。光電子の質量を \(m\) [kg]
光電子というのは電子のことであり、その質量は 9.1 × 10-31 [kg] ですがここでは \(m\) と置きます。
あと、光電子には質量がありますが光子には質量はありません。
、速度を \(v\) [m/s] とすると運動エネルギーは \({\large\frac{1}{2}}mv^2\) [J] であり、原子核からの引力を振りほどくためのエネルギーを \(W\) [J] と置くと、
\(hν\) = \({\large\frac{1}{2}}mv^2 + W\)
となります。\({\large\frac{1}{2}}mv^2\) を \(K_{\rm{\small M}}\) と置き
\(K\) は kinetic(運動の)の頭文字、M は max の頭文字のつもりです。
様々な運動エネルギーを持った光電子のうち、最大の運動エネルギーを持ったものに着目します。上の『運動エネルギーの最大値に着目』を参照してください。速度を \(v\) と置きましたが、本当は \(v_{\rm {\tiny M}}\) と置きたかったくらいです。
、移項して、
\(K_{\rm{\small M}}\) = \(hν - W\) ……①
と表現する場合もあります。
\(W\) には名前が付いていて仕事関数といいます
なんだか違和感のある名前です。英語の work function を直訳したものと思いますが、なぜ function なのか分かりません。
(その後読者の方に、\(W\) = \(hν - K\) と捉えれば \(K\) の関数とみなせる、とご指摘いただきました。)
。光によって電子が原子核の引力から振りほどかれるエネルギーです。仕事関数は光電効果の起こりやすさを表す値であり、金属の種類によって決まっています。
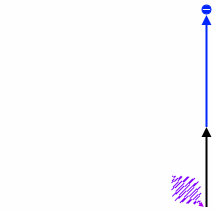
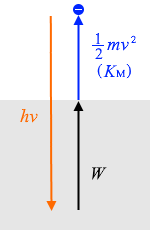 上式を矢印の長さで表現すればこんな感じになります。
上式を矢印の長さで表現すればこんな感じになります。
\(K_{\rm{\small M}}\)-\(ν\)グラフ
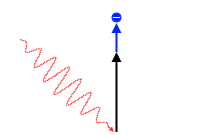 \(hν\) を粒っぽく描いて表現すればこんな感じになり、
\(hν\) を粒っぽく描いて表現すればこんな感じになり、
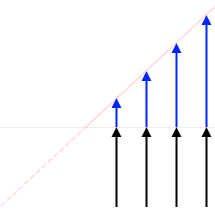
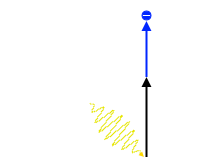 光の振動数 \(ν\) が大きくなっていく(=波長が小さくなっていく)につれて、
光の振動数 \(ν\) が大きくなっていく(=波長が小さくなっていく)につれて、
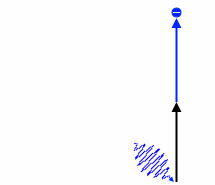 こんな感じになっていくと考えれば
こんな感じになっていくと考えれば
 振動数の大きい光子ほど玉っぽくなっていて電子を勢いよく跳ね飛ばすイメージがつかめるのではないでしょうか。(ムリか?)
振動数の大きい光子ほど玉っぽくなっていて電子を勢いよく跳ね飛ばすイメージがつかめるのではないでしょうか。(ムリか?)
 これらのことをまとめると、
これらのことをまとめると、
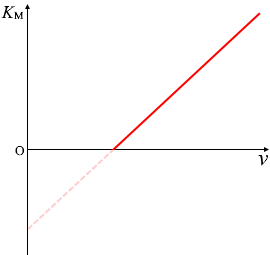 このようなグラフになります。光電子の運動エネルギーを表すグラフです。横軸は振動数です。
このようなグラフになります。光電子の運動エネルギーを表すグラフです。横軸は振動数です。
この曲線は、傾きが \(h\) の \(K_{\rm{\small M}}\) = \(hν\) という曲線
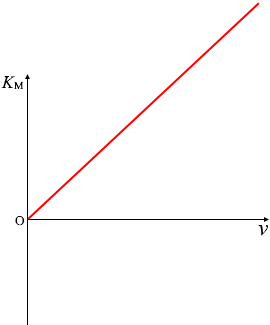 を下に \(W\) だけ平行移動させたもの(\(K_{\rm{\small M}}\) = \(hν - W\))になっています。つまり、傾きがプランク定数 \(h\) になっていて、縦軸の切片の絶対値が仕事関数 \(W\) になっています。下で説明しますが横軸の切片は限界振動数 \(ν_0\) になっています。薄い点線部分では光電効果は起こらず電子が飛び出すことはありません。
を下に \(W\) だけ平行移動させたもの(\(K_{\rm{\small M}}\) = \(hν - W\))になっています。つまり、傾きがプランク定数 \(h\) になっていて、縦軸の切片の絶対値が仕事関数 \(W\) になっています。下で説明しますが横軸の切片は限界振動数 \(ν_0\) になっています。薄い点線部分では光電効果は起こらず電子が飛び出すことはありません。
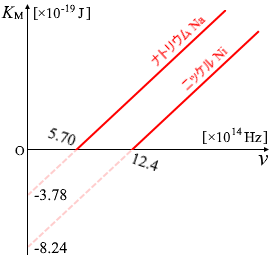 たとえば金属がナトリウムとニッケルの場合、グラフは左図のようになります。
たとえば金属がナトリウムとニッケルの場合、グラフは左図のようになります。
ナトリウムの方が仕事関数が小さく、光電効果が起こりやすくなってます。
振動数が \(ν_0\) のとき
光の振動数 \(ν\) が上の『光電効果の性質』で説明した限界振動数 \(ν_0\) であるときは、光電効果がギリギリ起こるかどうかというときで、飛び出す光電子の速度 \(v\) が 0 のときです。つまり \({\large\frac{1}{2}}mv^2\) (= \(K_{\rm{\small M}}\)) = 0 であり、これらを①式 \(K_{\rm{\small M}}\) = \(hν - W\) に代入すると、
\(hν_0\) = \(W\) ……②
です。\(ν\) がこの \(ν_0\) より小さいときは光電効果が起こりません。
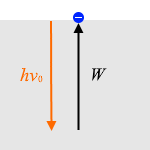 \(ν\) = \(ν_0\) のときの様子を矢印の長さで表現すればこんな感じになります。
\(ν\) = \(ν_0\) のときの様子を矢印の長さで表現すればこんな感じになります。
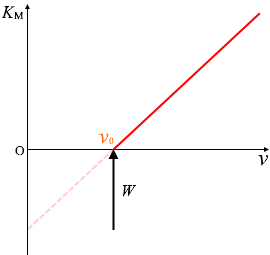 光電子の運動エネルギーのグラフでいうと左図のような部分のことになります。
光電子の運動エネルギーのグラフでいうと左図のような部分のことになります。
\(K_{\rm{\small M}}\) = \(h(ν - ν_0)\)
また、上の②式 \(hν_0\) = \(W\) を①式 \(K_{\rm{\small M}}\) = \(hν - W\) に代入すると以下のように表せます。
\(K_{\rm{\small M}}\) = \(hν - hν_0\)
= \(h(ν - ν_0)\)
さらに、\(ν\) = \({\large\frac{c}{λ}}\) 、\(ν_0\) = \({\large\frac{c}{λ_0}}\) を代入すれば
\(K_{\rm{\small M}}\) = \(hc({\large\frac{1}{λ}}\) - \({\large\frac{1}{λ_0}})\)
とも表せます。
プランク定数を求める実験
上の『光電管による光電効果』で紹介した実験は、プランク定数を求めるための実験でもあります。
この実験をミリカンの実験といいます。ミリカンの油滴実験と同一人物のロバート・ミリカンです。ミリカンはこの2つの実験で有名です。単に「ミリカンの実験」というと「プランク定数を求めるミリカンの光電効果の実験」なのか「電気素量を求めるミリカンの油滴実験」なのかどちらを指すのかハッキリしません。が、油滴実験の方がちょっと有名です。
 上で説明したように、しぼりとフィルターを固定し接点Dを動かすと左図のようなグラフが得られますが、このときの光電子の様子がどうなっているかといいますと、
上で説明したように、しぼりとフィルターを固定し接点Dを動かすと左図のようなグラフが得られますが、このときの光電子の様子がどうなっているかといいますと、
光電管内の光電子の様子
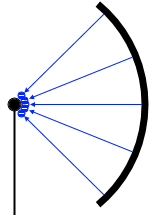 接点DがEに近いときというのは陽極の電位が高く、電場の向きは陽極から陰極への向きであり、電子の電荷は負であるので、光電子は陰極から陽極の方向へ静電気力(クーロン力)を受けます
正電荷であれば電場の方向へ力を受けますが、負電荷の場合は電場と逆の方向へ力を受けます。
。よって陰極から飛び出した光電子たちは余裕で陽極にたどり着きます。
接点DがEに近いときというのは陽極の電位が高く、電場の向きは陽極から陰極への向きであり、電子の電荷は負であるので、光電子は陰極から陽極の方向へ静電気力(クーロン力)を受けます
正電荷であれば電場の方向へ力を受けますが、負電荷の場合は電場と逆の方向へ力を受けます。
。よって陰極から飛び出した光電子たちは余裕で陽極にたどり着きます。
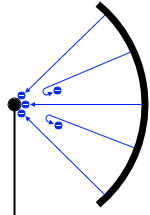 しかし接点Dが中央付近にあるときは、陽極と陰極の電位が同じくらいで電場は弱く、陽極にたどり着く光電子も少なくなり、
しかし接点Dが中央付近にあるときは、陽極と陰極の電位が同じくらいで電場は弱く、陽極にたどり着く光電子も少なくなり、
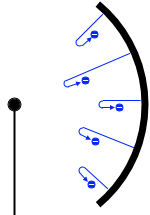 接点DがF寄りにあるときは、陽極の電位は負になっており、電場の向きは陰極から陽極への向きになり、負電荷である光電子は逆向きの静電気力を受け、なかなか陽極にたどり着かなくなります。
接点DがF寄りにあるときは、陽極の電位は負になっており、電場の向きは陰極から陽極への向きになり、負電荷である光電子は逆向きの静電気力を受け、なかなか陽極にたどり着かなくなります。
電流が 0 になるときの電圧
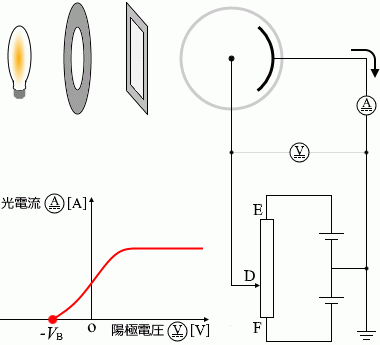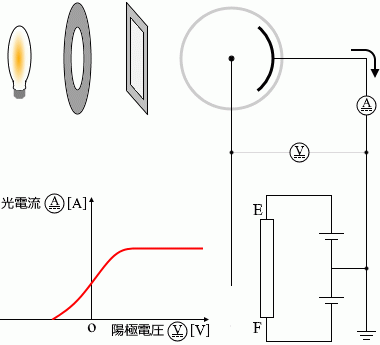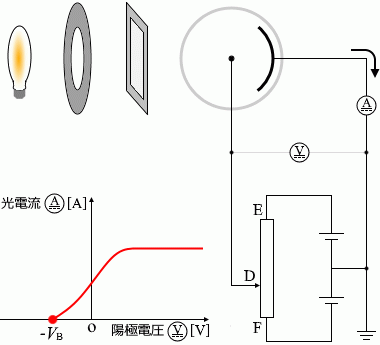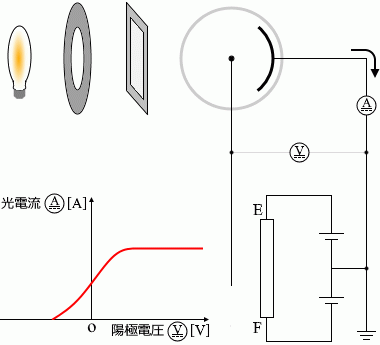 陰極を飛び出すときのスピードが最も大きい光電子(上の『運動エネルギーの最大値に着目』で説明した最大の運動エネルギーを持つ光電子)が陽極にたどり着くかどうかギリギリのときというのは電流が 0 かどうかギリギリのときのことでありますが、このときの電圧を阻止電圧といいます。\(V_{\rm{\small B}}\) [V] と置きます。
B は blocking の頭文字のつもりです。
陰極を飛び出すときのスピードが最も大きい光電子(上の『運動エネルギーの最大値に着目』で説明した最大の運動エネルギーを持つ光電子)が陽極にたどり着くかどうかギリギリのときというのは電流が 0 かどうかギリギリのときのことでありますが、このときの電圧を阻止電圧といいます。\(V_{\rm{\small B}}\) [V] と置きます。
B は blocking の頭文字のつもりです。
阻止電圧という言葉が
\(V_{\rm{\small B}}\) のことを指すのか
\({\small -}V_{\rm{\small B}}\) のことを指すのか
厳密な定義は分かりません。
\({\large\frac{1}{2}}mv^2\) = \(mgh\) のような話
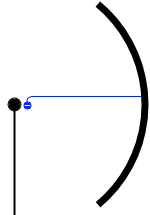 そうしますと、この光電子の位置エネルギーは
そうしますと、この光電子の位置エネルギーは
\(eV_{\rm{\small B}}\) [J]
ということになります。\(q\) の電荷が \(E\) の電場の中を \(d\) だけ進んだときのエネルギーは \(qEd\) であるわけですが、今、光電子の電荷は \({\small -}e\) であり、\(Ed\) というのは電位差のことでありそれは \({\small -}V_{\rm{\small B}}\) であるからです。
陰極を \(v\) で飛び出る瞬間の運動エネルギーが \({\large\frac{1}{2}}mv^2\) で、陽極へと進むにつれてスピードが落ちていき、運動エネルギーが 0 になっていくわけですが、その間に増える位置エネルギーが \(eV_{\rm{\small B}}\) ということです。
 このことは鉛直上方投射におけるエネルギーの関係に似ています。
このことは鉛直上方投射におけるエネルギーの関係に似ています。
初速 \(v\) で打ち上げられた瞬間の小球の運動エネルギーは \({\large\frac{1}{2}}mv^2\) であり、速度が小さくなるにつれて運動エネルギーが小さくなっていき、最上点では運動エネルギーが 0 になり、位置エネルギーが \(mgh\) になります。力学的エネルギー保存の法則です。\({\large\frac{1}{2}}mv^2\) = \(mgh\) であり、到達した高さ \(h\) から初速 \(v\) が割り出せたりします。
\(m\)\(gh\) と \(e\)\(V_{\rm{\small B}}\) を見比べると、\(m\) が \(e\) に、\(gh\) が \(V_{\rm{\small B}}\) に相当します。
というわけで、
\(K_{\rm{\small M}}\) = \({\large\frac{1}{2}}mv^2\) = \(eV_{\rm{\small B}}\) ……③
です。
電流が 0 になるときの電圧を\(e\)倍すると運動エネルギーになり、そこからグラフが描ける
これは阻止電圧の大きさにより \(K_{\rm{\small M}}\) の値が定まるということであり、
 フィルターを変えて(\(ν\) を変えて)阻止電圧を測定することにより、なんでもいいから (\(ν_1\) , \(V_{\rm{\small B1}}\)) と (\(ν_2\) , \(V_{\rm{\small B2}}\)) の2組の値を得れば、
フィルターを変えて(\(ν\) を変えて)阻止電圧を測定することにより、なんでもいいから (\(ν_1\) , \(V_{\rm{\small B1}}\)) と (\(ν_2\) , \(V_{\rm{\small B2}}\)) の2組の値を得れば、
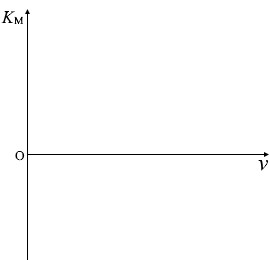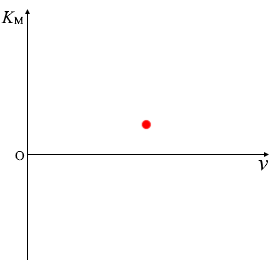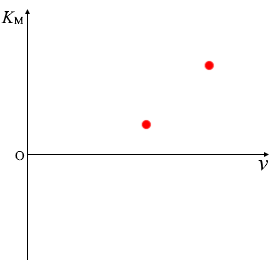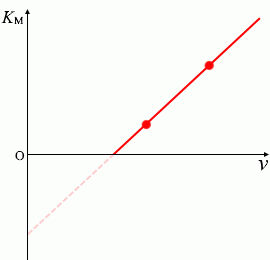 \(K_{\rm{\small M}}\)-\(ν\)グラフを描くことができ、曲線の傾きであるプランク定数 \(h\) を求めることができます。
\(K_{\rm{\small M}}\)-\(ν\)グラフを描くことができ、曲線の傾きであるプランク定数 \(h\) を求めることができます。
(参考書によってはグラフの縦軸が \(V\) [V] となっていることがありますが、\(V\) はここでいう \(V_{\rm{\small B}}\) のことで、\(V_{\rm{\small B}}\) は\(e\)倍すれば \(K_{\rm{\small M}}\) なのでグラフとしてはまったく同じ意味のものです)
式で説明
①式 \(K_{\rm{\small M}}\) = \(hν - W\) に③式 \(K_{\rm{\small M}}\) = \(eV_{\rm{\small B}}\) を代入して、
\(eV_{\rm{\small B}}\) = \(hν - W\)
(\(ν_1\) , \(V_{\rm{\small B1}}\)) と (\(ν_2\) , \(V_{\rm{\small B2}}\)) の値を代入し、
\(eV_{\rm{\small B1}}\) = \(hν_1 - W\) ……④
\(eV_{\rm{\small B2}}\) = \(hν_2 - W\) ……⑤
上式から下式を引いて、
\(eV_{\rm{\small B1}} - eV_{\rm{\small B2}}\) = \(hν_1 - hν_2\)
∴ \(e(V_{\rm{\small B1}} - V_{\rm{\small B2}})\) = \(h(ν_1 - ν_2)\)
∴ \(h\) = \(e{\large\frac{V_{\rm{\small B1}}-V_{\rm{\small B2}}}{ν_1-ν_2}}\)
この式に各測定値を代入すればプランク定数 \(h\) が求まります。
また、この式を④式か⑤式に代入し直すと、
\(eV_{\rm{\small B1}}\) = \(hν_1 - W\)
∴ \(W\) = \(hν_1 - eV_{\rm{\small B1}}\)
= \(e{\large\frac{V_{\rm{\small B1}}-V_{\rm{\small B2}}}{ν_1-ν_2}}ν_1 - eV_{\rm{\small B1}}\)
= \(e{\large\frac{V_{\rm{\small B1}}-V_{\rm{\small B2}}}{ν_1-ν_2}}ν_1 - eV_{\rm{\small B1}}{\large\frac{ν_1-ν_2}{ν_1-ν_2}}\)
= \(e{\large\frac{V_{\rm{\small B1}}ν_1-V_{\rm{\small B2}}ν_1-V_{\rm{\small B1}}ν_1+V_{\rm{\small B1}}ν_2}{ν_1-ν_2}}\)
= \(e{\large\frac{V_{\rm{\small B1}}ν_2-V_{\rm{\small B2}}ν_1}{ν_1-ν_2}}\)
と、仕事関数 \(W\) を求める式となります。
電子ボルト
エネルギーの単位として今までは J ジュール を用いてきましたが、原子分野では eV 電子ボルト(エレクトロンボルト)という単位を多用します。
1個の電子が 1V の電位差で加速されたときに得る運動エネルギーが 1eV 、と定義されています。
距離は関係ありません。
50cm の区間で 1V の電位差があるときでも、3m の区間で 1V の電位差があるときでも同じです。
上でも説明したように、\(q\) [C] の電荷が \(V\) [V] の電位差で加速されるとエネルギーは \(qV\) [J] です。ということは電子1個が 1V の電位差で加速されると \(e\) × 1 = \(e\) [J] です。
つまり、
1 [eV] = \(e\) [J]
です。\(e\) [C] × 1 [V] = \(e\) [J] であることを含めてこれを表現すれば、
1 [eV] = \(e\) [C] × 1 [V] = \(e\) [J]
です。
右辺の \(e\) というのは量記号ではなく定数です
\(g\) や \(π\) や \(c\) と同じです。
。1.6×10-19 という数値です。つまり、
1 [eV] = 1.6×10-19 [J]
です。両辺を 1.602176634×10-19 で割れば、おおよそ
1 [J] = 6.242 × 1018 [eV]
です。[eV] という単位は [J] に比べてとても小さい単位です。
慣れるまではややこしい
電子1個が \(V\) [V] の電位差で加速されるとエネルギーは
\(eV\) [J]
ですが、単位を [eV] に変換すると(\(e\) で割って)
\(V\) [eV]
です。つまり、
\(eV\) [J] = \(V\) [eV]
です。
\(e\) [C] の \(e\) は定数であり(画面上、紙面上)斜体で表示します(しています)。\(eV\) [J] や \(V\) [eV] の \(V\) は量記号であり、これも斜体で表示します。[eV] の eV は単位であり、立体で表示します。ややこしいです。
試験の際、答案用紙に斜体と立体を厳密に区別しながら記述する必要はないと思います。
そもそも \(e\) や \(g\) や \(π\) などの定数はルール的には立体で書くべきもののようです。でも立体で書いてある教科書は見たことがありません。インターネットでは立体で書いているのを見かけたことがありますが…。\(m\)g と表記していました(\(m\) が斜体で g が立体)。
プランク定数なんかは h を斜めにしたフォントが用意されていたりします。定数であるはずなのに斜体です。わけが分かりません。
メガ電子ボルトなど
eV は1000倍ずつしていくと、
keV キロ電子ボルト
MeV メガ電子ボルト
GeV ギガ電子ボルト
TeV テラ電子ボルト
1/1000ずつしていくと、
meV ミリ電子ボルト
μeV マイクロ電子ボルト
などとなります。
 箔検電器の上にアルミ板または亜鉛板を載せ
アルミニウムや亜鉛は仕事関数(下で説明)が小さく、
箔検電器の上にアルミ板または亜鉛板を載せ
アルミニウムや亜鉛は仕事関数(下で説明)が小さく、 そこに紫外線を当てると箔が閉じます。負電荷が減ったのです。減ったのは上部の金属板から負電荷の電子が飛び出したためです。
箔検電器を負ではなく正に帯電させたときは
そこに紫外線を当てると箔が閉じます。負電荷が減ったのです。減ったのは上部の金属板から負電荷の電子が飛び出したためです。
箔検電器を負ではなく正に帯電させたときは 光電管とは陽極(正極)と陰極(負極)を内蔵した真空のガラス管で
陰極には亜鉛よりもっと仕事関数が小さくて光電効果を起こしやすい金属が用いられます。
光電管とは陽極(正極)と陰極(負極)を内蔵した真空のガラス管で
陰極には亜鉛よりもっと仕事関数が小さくて光電効果を起こしやすい金属が用いられます。
 しぼりを固定し、フィルターも1種類に定めた上で、接点Dを動かすと電圧計と電流計の値は左のグラフのように変化します。電圧が 0 であっても電流は流れます。接点DをFに近づけていくと(陽極の電位を低くしていくと)ある時点で電流は流れなくなります
光電子が進行方向と逆向きの静電気力を受けるためです。
しぼりを固定し、フィルターも1種類に定めた上で、接点Dを動かすと電圧計と電流計の値は左のグラフのように変化します。電圧が 0 であっても電流は流れます。接点DをFに近づけていくと(陽極の電位を低くしていくと)ある時点で電流は流れなくなります
光電子が進行方向と逆向きの静電気力を受けるためです。 しぼりを拡げて光の強さを2倍にすると光電流も2倍になります
光の強さを2倍にするということは光子の個数を2倍にするということです。
しぼりを拡げて光の強さを2倍にすると光電流も2倍になります
光の強さを2倍にするということは光子の個数を2倍にするということです。 フィルターの色を赤→黄→青→紫と変えていくと
フィルターの色が赤色のときに光電効果が起こるような金属はあまりないです。セシウム Cs くらいでしょうか。
フィルターの色を赤→黄→青→紫と変えていくと
フィルターの色が赤色のときに光電効果が起こるような金属はあまりないです。セシウム Cs くらいでしょうか。 このことと同じように、陰極に用いる金属の種類を変えた場合も左図のように曲線が変化します。
このことと同じように、陰極に用いる金属の種類を変えた場合も左図のように曲線が変化します。 上式を矢印の長さで表現すればこんな感じになります。
上式を矢印の長さで表現すればこんな感じになります。 \(hν\) を粒っぽく描いて表現すればこんな感じになり、
\(hν\) を粒っぽく描いて表現すればこんな感じになり、 光の振動数 \(ν\) が大きくなっていく(=波長が小さくなっていく)につれて、
光の振動数 \(ν\) が大きくなっていく(=波長が小さくなっていく)につれて、 こんな感じになっていくと考えれば
こんな感じになっていくと考えれば 振動数の大きい光子ほど玉っぽくなっていて電子を勢いよく跳ね飛ばすイメージがつかめるのではないでしょうか。
振動数の大きい光子ほど玉っぽくなっていて電子を勢いよく跳ね飛ばすイメージがつかめるのではないでしょうか。 これらのことをまとめると、
これらのことをまとめると、 このようなグラフになります。光電子の運動エネルギーを表すグラフです。横軸は振動数です。
このようなグラフになります。光電子の運動エネルギーを表すグラフです。横軸は振動数です。
 たとえば金属がナトリウムとニッケルの場合、グラフは左図のようになります。
たとえば金属がナトリウムとニッケルの場合、グラフは左図のようになります。 \(ν\) = \(ν_0\) のときの様子を矢印の長さで表現すればこんな感じになります。
\(ν\) = \(ν_0\) のときの様子を矢印の長さで表現すればこんな感じになります。 光電子の運動エネルギーのグラフでいうと左図のような部分のことになります。
光電子の運動エネルギーのグラフでいうと左図のような部分のことになります。 接点DがEに近いときというのは陽極の電位が高く、
接点DがEに近いときというのは陽極の電位が高く、 しかし接点Dが中央付近にあるときは、陽極と陰極の電位が同じくらいで電場は弱く、陽極にたどり着く光電子も少なくなり、
しかし接点Dが中央付近にあるときは、陽極と陰極の電位が同じくらいで電場は弱く、陽極にたどり着く光電子も少なくなり、 接点DがF寄りにあるときは、陽極の電位は負になっており、電場の向きは陰極から陽極への向きになり、負電荷である光電子は逆向きの静電気力を受け、なかなか陽極にたどり着かなくなります。
接点DがF寄りにあるときは、陽極の電位は負になっており、電場の向きは陰極から陽極への向きになり、負電荷である光電子は逆向きの静電気力を受け、なかなか陽極にたどり着かなくなります。 陰極を飛び出すときのスピードが最も大きい光電子(上の『
陰極を飛び出すときのスピードが最も大きい光電子(上の『 そうしますと、この光電子の位置エネルギーは
そうしますと、この光電子の位置エネルギーは このことは鉛直上方投射におけるエネルギーの関係に似ています。
このことは鉛直上方投射におけるエネルギーの関係に似ています。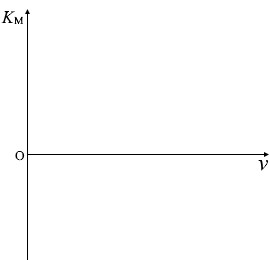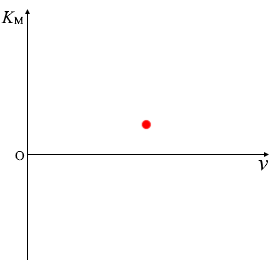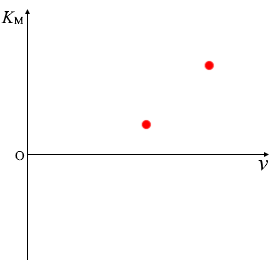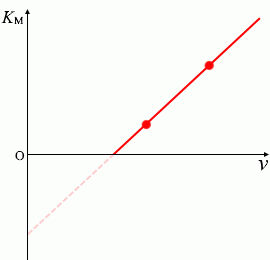 \(K_{\rm{\small M}}\)-\(ν\)グラフを描くことができ、曲線の傾きであるプランク定数 \(h\) を求めることができます。
\(K_{\rm{\small M}}\)-\(ν\)グラフを描くことができ、曲線の傾きであるプランク定数 \(h\) を求めることができます。