X線をスリットを通して結晶に照射し、その背後にフィルムを置くと、幾何学模様の斑点が写ります。ラウエ斑点といいます
1879年–1960年のドイツの物理学者
マックス・フォン・ラウエが発見しました。
。
これは結晶中の原子間の距離と同じくらいの波長の電磁波（X線）の回折によってできるもので、この現象をX線回折といいます
”回折”という表現について、
「巨視的に見ると回折だが微視的に厳密に見ると散乱と干渉である」と考える人がいるかもしれませんが、
回折は干渉の一種と言えなくもないので回折という用語が不適切とは言い切れないです。
。
斑点模様は結晶構造を反映するので結晶内部の原子配列を調べるときにX線回折が用いられます。
X線回折による結晶構造解析です。回折（かいせつ）による解析（かいせき）です。
既知の結晶を用いてその写った模様からX線の波長を求めることにも利用されます。
結晶中の原子は規則的に並んでいますが、
X線がそれらの原子に当たると散乱し、原子を中心とした球面波ができます。
重ね合わせた波
原子が規則的に並んでいるからこそ
重ね合わせたときに綺麗な平面（左図においては直線）になります。
は
入射した角度と同じ角度で反射します。
別の言い方をしますと、入射X線と同じ角度で反射したX線は位相が揃っている、となります。
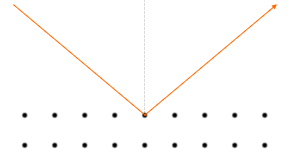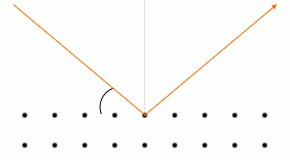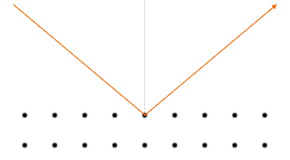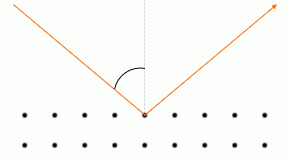一般的な波の反射においては法線とのなす角をその角度と定めますが、X線回折においては平面とのなす角をその角度と定めることが多いです。
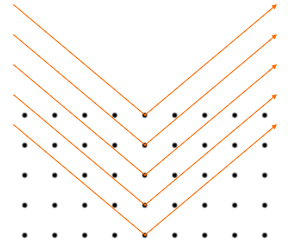X線は強い透過性を持つので、このような反射は1段目の格子面
原子を連ねた平面を格子面といいます。
だけでなく2段目、3段目、4段目、…でも起こります。
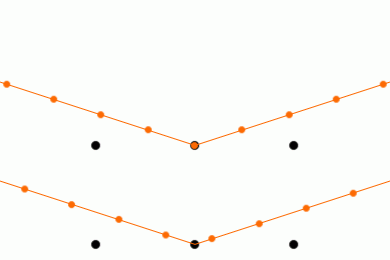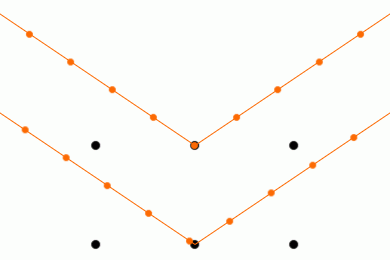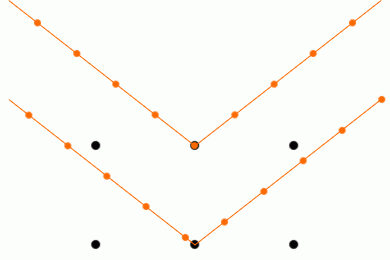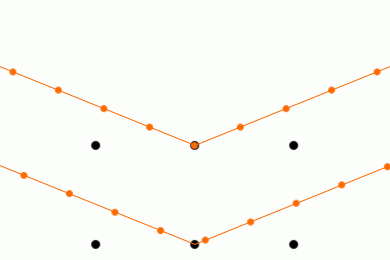そうすると角度によっては
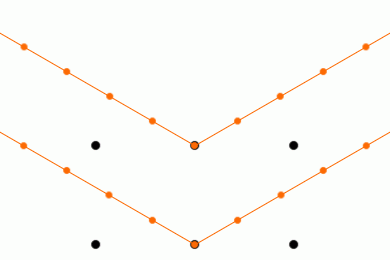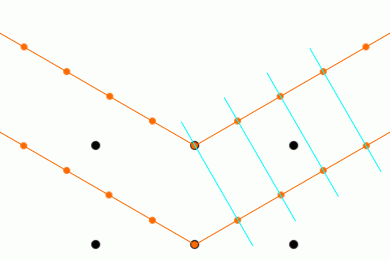反射X線の位相が揃って強め合います
弱め合う
強め合う
（左図はX線を
ではなく
と描いています
説明のためにX線を様々な形で表現しています。
とか、
とか、
とか、
とか。
どれもX線のことを表しています。
）。ヤングの干渉実験や回折格子と同じ原理です。
この図を見てもらうと、波長の大きさと原子間の距離（≒格子面の間隔）が同じくらいの（100倍とか1000倍とかの差がない）ときに回折が起こりやすいことが分かると思います。
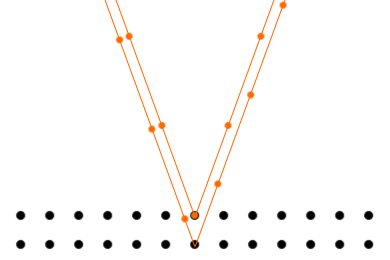原子間距離に対して波長が大きすぎるときは曲げても位相が揃いません。
下で説明するブラッグの条件の式
\(2d\sinθ\) = \(nλ\)
の \(θ\) の最大値は 90° であり、\(\sinθ\) の最大値は 1 です。
つまり、
\(2d⋅1\) ≧ \(nλ\)
であり、\(n\) = 1 のとき（経路差が1波長となるとき）
\(2d⋅1\) ≧ \(1⋅λ\)
∴ \(2d\) ≧ \(λ\)
であり、つまりX線の波長 \(λ\) が格子面の間隔（≒原子間の距離）の2倍以下でなければブラッグ反射は起こらない（強め合わない）のです。
反対に、原子間距離に対して波長が小さすぎるときはブラッグの条件の式における \(n\) の値が 100 とか 1000 とかという値を取りうることになり（回折格子でいうところの100次、1000次の干渉縞）、一つひとつのエネルギーは小さくなり（一つひとつの縞は薄くなり）、斑点を観測するのは難しくなります。
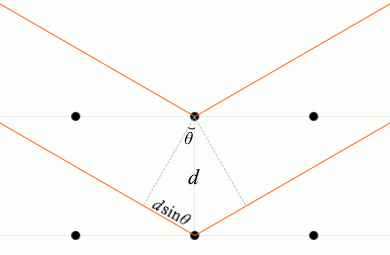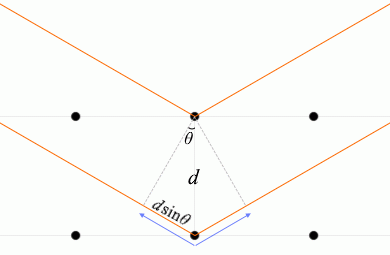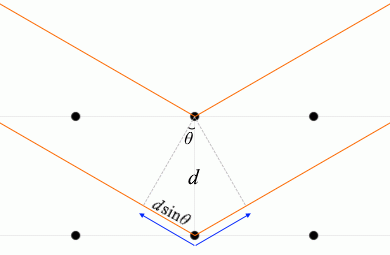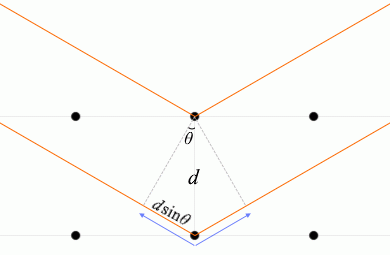入射X線と格子面とのなす角を \(θ\) 、格子面の間隔を \(d\) としますと、隣接する格子面での2つの反射波の経路差 ↖↗ は \(2d\sinθ\) です
。
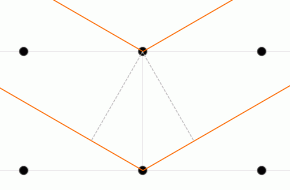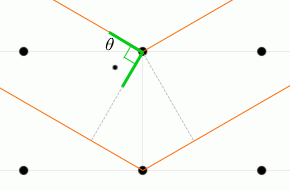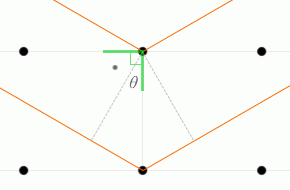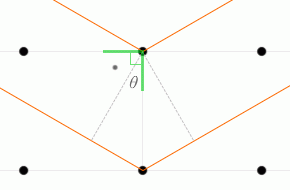
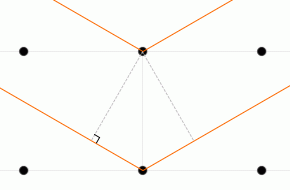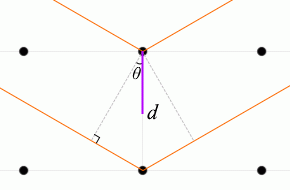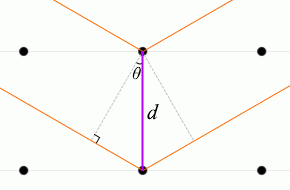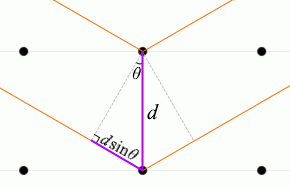
この経路差がX線の波長 \(λ\) の自然数倍
ヤングの実験や回折格子のときは0倍のときも強め合います（0次の干渉縞）がブラッグ反射では0倍のときというのは無いので「整数倍」ではなく「自然数倍」です。
反射せずにまっすぐ突き抜ける場合を0倍、とすれば「整数倍」という考え方も有りえます。
になると反射X線は強め合います。
ブラッグの条件
\(\boldsymbol{2d\sinθ}\) = \(\boldsymbol{nλ}\) (\(n\) = 1,2,3,…)
この条件を満たす反射をブラッグ反射 イギリスの物理学者ヘンリー・ブラッグ（1862年–1942年）とローレンス・ブラッグ（1890年–1971年）の父子が発見しました。 といいます。
ブラッグ反射を起こす格子面というのは
このような方向だけでなく
色々な方向があります。
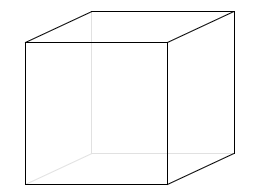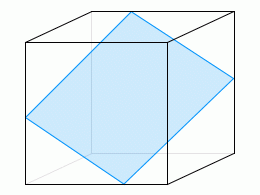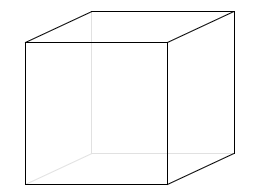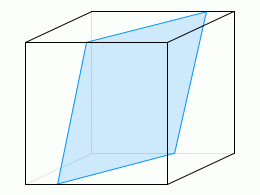2次元でなく3次元に拡張するともっとたくさんあります。
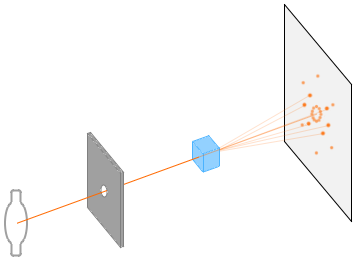というわけで結晶後方に置いたフィルムにはたくさんの点が写り、その模様は結晶構造を反映したものになります。
この球面波は