コンプトン効果
コンプトン効果とは
X線を物質に当てると散乱しますが、散乱X線の中には入射X線より波長の長いものが含まれます。この現象をコンプトン効果といいます
1892年–1962年のアメリカの物理学者、アーサー・コンプトンが発見しました。
コンプトン効果による散乱をコンプトン散乱といいます。
散乱X線の中に入射X線より波長の短いX線が含まれることもあり、逆コンプトン効果といわれます。高校物理では扱いません。
。X線が純粋な波動であれば入射X線と散乱X線の波長は同じになるはずですが、そうでないのはX線が粒子性を持ち、衝突後のX線のエネルギーが減る（＝振動数が小さくなる＝波長が大きくなる
エネルギーの式
\(E = hν = {\large\frac{hc}{λ}}\)
において \(E\) が小さくなるということは \(ν\) が小さくなって \(λ\) が大きくなるということです。\(h\) と \(c\) は定数です。
）ためと考えられます。
光子のエネルギーと運動量
コンプトンはX線が光子という粒子の流れであり、運動の前後でエネルギー保存の法則と運動量保存の法則が成り立つと考えました。
光子1個のエネルギーを \(E\) [J]、プランク定数を \(h\) [J⋅s]、振動数を \(ν\) [Hz]、波長を \(λ\) [m]、光速を \(c\) [m/s] とすると、光子のエネルギーは光量子仮説より
\[E = hν = \frac{hc}{λ}\]です。
光子1個の運動量については、上式に相対性理論の式 \(E = mc^2\) を代入して、
\[mc^2 = hν\]両辺を \(c\) で割って、
\(∴\ \ mc = {\Large\frac{hν}{c}}\)
左辺は質量×速度になっているからこれは運動量であり、これを \(p\) とすると、
光子1個の運動量
\(\boldsymbol{p}\) = \(\boldsymbol{{\large\frac{hν}{c}}}\) = \(\boldsymbol{{\large\frac{h}{λ}}}\)
となります。ちょっと強引な導出ですが厳密なことは大学に行って学んでください
特に \({\large\frac{1}{2}}\) がどこへ消えたか気になるかもしれません。
物体の運動エネルギーは
\({\large\frac{1}{2}}mv^2\)
で、運動量は
\(mv\)
なのだから運動エネルギーに 2 を掛けて速度 \(v\) で割ったものが運動量になるはずが、光子の場合は単純に速度 \(c\) で割っただけのものになっています。
これは \(v\) と \(c\) の違いからくるもので、だからといって \(v = {\large\frac{1}{2}}c\) というわけでもなく、ちょっと難しい話で説明できません。大学に行って学んでください。
。
単位は、上式 \(p = {\large\frac{h}{λ}}\) より、[J⋅s/m] です。もちろん運動量ですから [kg⋅m/s] でもあります。
式を覚えるのが大変ですが、まず \(E = hν\) を覚えて、「運動量はエネルギーを速度で割ったものだから」と \(p = {\large\frac{hν}{c}}\) を導き出して、それらに \(v\) = \(fλ\) の式である \(c = νλ\) を代入して他の式を導き出すようにしてください。
この \(E\) と \(p\) が運動の前後で変わらないとコンプトンは考えたわけです。
エネルギー保存則と運動量保存則から波長の伸びを求める
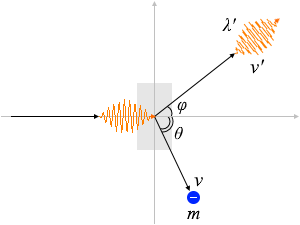この図は1個のX線光子が物質中の1個の電子に衝突し、跳ね飛ばした場面を表しています。
コンプトンはX線を当てる物質として石墨（せきぼく=グラファイト＝黒鉛）を用いました。他に銅や銀なども用いましたが、それらを使っても散乱X線の波長のズレの大きさは変わりませんでした。
このとき光子のエネルギーが小さくてそれが電子の運動エネルギーとして全て吸収されてしまう場合が光電効果で、光子のエネルギーが大きくて電子と衝突した後でも光子として残って散乱するのがコンプトン効果です（ざっくりした説明ですが）。
散乱X線の波長を \(λ'\) [m]、振動数を \(ν\ '\) [Hz]、入射方向と散乱方向とのなす角（散乱角）を \(φ\) 、電子の質量を \(m\) [kg]、跳ね飛ばされた電子の速さを \(v\) [m/s]、入射方向と跳ね飛ばされた方向とのなす角を \(θ\) とします。
（以下計算が長いですが内容は簡単です）
（エネルギー保存の法則）
衝突前のエネルギーは
\({\large\frac{hc}{λ}}\)
衝突後のエネルギーは
\({\large\frac{hc}{λ'}} + {\large\frac{1}{2}}mv^2\)
エネルギーが保存されるとしますと、
\({\large\frac{hc}{λ}} = {\large\frac{hc}{λ'}} + {\large\frac{1}{2}}mv^2\)
（\(ν\) を使った別の表現）
衝突前のエネルギーは
\(hν\)
衝突後のエネルギーは
\(hν\ ' + {\large\frac{1}{2}}mv^2\)
エネルギーが保存されるとしますと、
\(hν = hν\ ' + {\large\frac{1}{2}}mv^2\)
……①
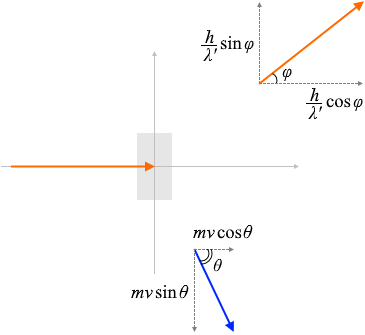（入射方向の運動量保存の法則）
衝突前の運動量は
\({\large\frac{h}{λ}}\)
衝突後の運動量は
\({\large\frac{h}{λ'}}\cosφ + mv\cosθ\)
運動量が保存されるとしますと、
\({\large\frac{h}{λ}} = {\large\frac{h}{λ'}}\cosφ + mv\cosθ\)
（\(ν\) を使った別の表現）
衝突前の運動量は
\({\large\frac{hν}{c}}\)
衝突後の運動量は
\({\large\frac{hν\ '}{c}}\cosφ + mv\cosθ\)
運動量が保存されるとしますと、
\({\large\frac{hν}{c}} = {\large\frac{hν\ '}{c}}\cosφ + mv\cosθ\)
……②
（入射方向に垂直な方向の運動量保存の法則）
衝突前の運動量は
\(0\)
衝突後の運動量は
\({\large\frac{h}{λ'}}\sinφ - mv\sinθ\)
運動量が保存されるとしますと、
\(0 = {\large\frac{h}{λ'}}\sinφ - mv\sinθ\)
（\(ν\) を使った別の表現）
衝突前の運動量は
\(0\)
衝突後の運動量は
\({\large\frac{hν\ '}{c}}\sinφ - mv\sinθ\)
運動量が保存されるとしますと、
\(0 = {\large\frac{hν\ '}{c}}\sinφ - mv\sinθ\)
……③
（別解）
運動量が保存されるということは
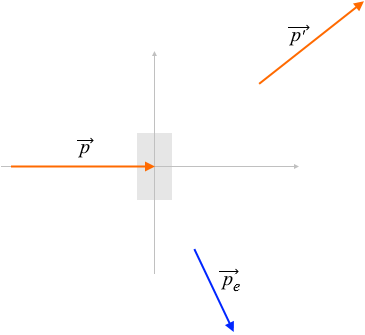
\(\vec{p} = \vec{p'} + \vec{p_e}\)
であり、すなわち
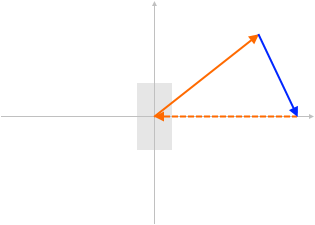
\(0 = \vec{p'} + \vec{p_e} - \vec{p}\)
であり、これは3つのベクトルで閉じた三角形ができるということであり、
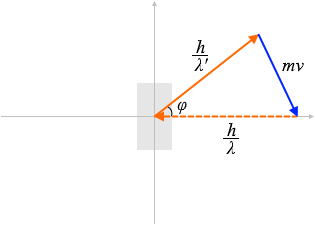
余弦定理（ \(a^2 = b^2 + c^2 - 2bc\cosα\) ）より、
\((mv)^2 = \Big({\large\frac{h}{λ}}\Big)^2 + \Big({\large\frac{h}{λ'}}\Big)^2 - 2\Big({\large\frac{h}{λ}}\Big)\Big({\large\frac{h}{λ'}}\Big)\cosφ\)
となるということです。
これに下の①'式を代入すると⑤式になります。
余弦定理を用いると計算が少しだけ楽になります。
②式を変形して、
\(mv\cosθ = {\large\frac{h}{λ}} - {\large\frac{h}{λ'}}\cosφ\) 両辺を2乗して
\((mv)^2\cos^2θ = \Big({\large\frac{h}{λ}} - {\large\frac{h}{λ'}}\cosφ\Big)^2\) ……②'
③式を変形して、
\(mv\sinθ = {\large\frac{h}{λ'}}\sinφ\) 両辺を2乗して
\((mv)^2\sin^2θ = \Big({\large\frac{h}{λ'}}\sinφ\Big)^2\) ……③'
②'式と③'式の辺々を足すと
\((mv)^2\cos^2θ + (mv)^2\sin^2θ = \Big({\large\frac{h}{λ}} - {\large\frac{h}{λ'}}\cosφ\Big)^2 + \Big({\large\frac{h}{λ'}}\sinφ\Big)^2\)
\(\cos^2θ + \sin^2θ = 1\) だから
\((mv)^2 = \Big({\large\frac{h}{λ}} - {\large\frac{h}{λ'}}\cosφ\Big)^2 + \Big({\large\frac{h}{λ'}}\sinφ\Big)^2\) ……④
①式を変形して、
\({\large\frac{1}{2}}mv^2 = {\large\frac{hc}{λ}} - {\large\frac{hc}{λ'}}\) 両辺に \(2m\) を掛けて
\((mv)^2 = 2m\Big({\large\frac{hc}{λ}} - {\large\frac{hc}{λ'}}\Big)\) ……①'
これを④式に代入すると、
\(2m\Big({\large\frac{hc}{λ}} - {\large\frac{hc}{λ'}}\Big) = \Big({\large\frac{h}{λ}} - {\large\frac{h}{λ'}}\cosφ\Big)^2 + \Big({\large\frac{h}{λ'}}\sinφ\Big)^2\)
\(∴\ 2mhc\textcolor{#bbb}{\Big({\large\frac{1}{λ}} - {\large\frac{1}{λ'}}\Big)} = h^2\textcolor{#bbb}{\Big({\large\frac{1}{λ}} - {\large\frac{1}{λ'}}\cosφ\Big)^2} + h^2\textcolor{#bbb}{\Big({\large\frac{1}{λ'}}\sinφ\Big)^2}\)
\(∴\ \ {\large\frac{2mc}{h}}\textcolor{#bbb}{\Big({\large\frac{1}{λ}} - {\large\frac{1}{λ'}}\Big)} = \textcolor{#bbb}{\Big({\large\frac{1}{λ}} - {\large\frac{1}{λ'}}\cosφ\Big)^2 + \Big({\large\frac{1}{λ'}}\sinφ\Big)^2}\)
\(= \Big({\large\frac{1}{λ}}\Big)^2 - 2\Big({\large\frac{1}{λ}}\Big)\Big({\large\frac{1}{λ'}}\cosφ\Big) + \Big({\large\frac{1}{λ'}}\cosφ\Big)^2\textcolor{#bbb}{+ \Big({\large\frac{1}{λ'}}\sinφ\Big)^2}\)
\(\Big(\)\(\cos^2φ + \sin^2φ = 1\) だから\(\Big)\)
\(= \textcolor{#bbb}{\Big({\large\frac{1}{λ}}\Big)^2 - 2\Big({\large\frac{1}{λ}}\Big)\Big({\large\frac{1}{λ'}}\cosφ\Big)} + \Big({\large\frac{1}{λ'}}\Big)^2\)
\(= \Big({\large\frac{1}{λ}}\Big)^2 + \Big({\large\frac{1}{λ'}}\Big)^2 \textcolor{#bbb}{- 2\Big({\large\frac{1}{λ}}\Big)\Big({\large\frac{1}{λ'}}\cosφ\Big)}\) ……⑤
\(= \textcolor{#bbb}{\Big({\large\frac{1}{λ}}\Big)^2 + \Big({\large\frac{1}{λ'}}\Big)^2} - 2\Big({\large\frac{1}{λ}}\Big)\Big({\large\frac{1}{λ'}}\Big) + 2\Big({\large\frac{1}{λ}}\Big)\Big({\large\frac{1}{λ'}}\Big) \textcolor{#bbb}{- 2\Big({\large\frac{1}{λ}}\Big)\Big({\large\frac{1}{λ'}}\cosφ\Big)}\)
\(= \Big({\large\frac{1}{λ}} - {\large\frac{1}{λ'}}\Big)^2 \textcolor{#bbb}{+ 2\Big({\large\frac{1}{λ}}\Big)\Big({\large\frac{1}{λ'}}\Big) - 2\Big({\large\frac{1}{λ}}\Big)\Big({\large\frac{1}{λ'}}\cosφ\Big)}\)
\(= \textcolor{#bbb}{\Big({\large\frac{1}{λ}} - {\large\frac{1}{λ'}}\Big)^2} + {\large\frac{2}{λλ'}}(1 - \cosφ)\)
\(⇔\ {\large\frac{2mc}{h}}\Big({\large\frac{1}{λ}} - {\large\frac{1}{λ'}}\Big) = \Big({\large\frac{1}{λ}} - {\large\frac{1}{λ'}}\Big)^2 + {\large\frac{2}{λλ'}}(1 - \cosφ)\)
\(∴\ \ \ \ \ \ \textcolor{#bbb}{{\large\frac{2mc}{h}}}\Big({\large\frac{λ'-λ}{λλ'}}\Big) = \Big({\large\frac{λ'-λ}{λλ'}}\Big)^2 \textcolor{#bbb}{+ {\large\frac{2}{λλ'}}(1 - \cosφ)}\)
\(\Big(\) \(λ\) と \(λ'\) の差が \(λ\) に比べて小さくて、\(λ' - λ\) は 0 とまではいえないが、\((λ' - λ)^2\) はほぼ 0 とみなせる場合\(\Big)\)
\(⇔\ \textcolor{#bbb}{{\large\frac{2mc}{h}}\Big({\large\frac{λ'-λ}{λλ'}}\Big)} = 0 \textcolor{#bbb}{+ {\large\frac{2}{λλ'}}(1 - \cosφ)}\)
\(∴\ \ \ \ {\large\frac{mc}{h}}(λ' - λ) = (1 - \cosφ)\)
\(∴\ \ \ \ \ \ \ \ \ \ \ \ \ \textcolor{#bbb}{λ' - λ} = {\large\frac{h}{mc}}\textcolor{#bbb}{(1 - \cosφ)}\)
左辺はコンプトン効果の波長の伸び（あるいは波長のズレ）といえるもので、\(⊿λ = λ' - λ\) と置きますとこの伸びは散乱角 \(φ\) を用いて以下のように表せます。
コンプトン効果の波長の伸び
\(\boldsymbol{⊿λ = {\large\frac{h}{mc}}(1 - \cosφ)}\)
この式は実験結果とよく一致しました。X線を粒子としてとらえ、エネルギー保存則や運動量保存則が成り立つと考えることが妥当であると証明されたわけです。
また、この式の右辺をよく見ると定数ばかりで構成されています。\(h\) も \(m\) も \(c\) も定数です。物質の種類に関する量も無いし、入射X線の波長 \(λ\) も出てきません。コンプトン効果の波長の伸びは散乱角 \(φ\) のみによって決まるのです
\(φ\) が大きいほど波長は伸び \(⊿λ\) は大きくなります。\(φ\) = 180° のときが最大です。
\(φ\) = 90° のときの \(⊿λ\) を特別にコンプトン波長といいます。
上式に \(φ\) = 90°、プランク定数 \(h\) = 6.6×10-34 [J⋅s]、電子の質量 \(m\) = 9.1×10-31 [kg]、光速 \(c\) = 3.0×108 [m/s] を代入しますと、
\(⊿λ = {\large\frac{h}{mc}}(1 - \cos90°)\)
\(⊿λ = {\large\frac{h}{mc}}(1 - 0)\)
\(⊿λ = {\large\frac{h}{mc}}\)
\(⊿λ = {\large\frac{6.6×10^{-34}}{9.1×10^{-31}×3.0×10^{8}}}\)
\(= {\large\frac{2.2}{9.1}}×10^{-34+31-8}\)
≒ 0.24×10-11
= 2.4×10-12 [m]
これがコンプトン波長です。「電子のコンプトン波長」ともいいます。
。