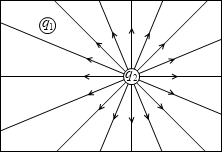
点電荷による電位

一様な電場より複雑

『電位』項では主に一様な電場での電位について考えましたが、本項では点電荷による電位について考えてみます。

電位というのは +1 C の電荷の位置エネルギーのことであるので、点電荷の近くに置かれた +1 C の電荷の位置エネルギーというものを導き出してみます。

クーロンの法則

　　　　F = k\(\large{\frac{q_1q_2}{r^2}}\)

の q₁ を +1 C の電荷、q₂ を正の点電荷であり電場の発生源とします。

位置エネルギーというのは、基準位置からその位置まで運ぶ仕事の量のことで、仕事の量というのは力と距離を掛け合わせたものです。もしこのときの力があらゆる地点で一定であるなら、『電位』項のように簡単に導き出せるのですが、点電荷による電場の場合は場所によって静電気力の大きさが違います。ですので導き方は『電位』項のように単純ではなく、万有引力による位置エネルギーのように複雑になります。

万有引力による位置エネルギーは、万有引力

　　　　F = G\(\large{\frac{Mm}{r^2}}\)

を r で積分して、

　　　　U = - G\(\large{\frac{Mm}{r}}\)

と導き出しました。クーロンの法則

　　　　F = k\(\large{\frac{q_1q_2}{r^2}}\)

は万有引力の法則とそっくりなので、r で積分する計算過程は万有引力による位置エネルギーを求める計算過程と一緒です。

　　　　G　→　k
　　　　m　→　q₁　→　+1
　　　　M　→　q₂　→　q （正）

と置き換わったと考えます。さらに k の前に -（マイナス）を付けます。万有引力は M と m が引き合う力でした。そしていま、静電気力を発揮する2つの電荷は両方とも正で、すなわち反発し合う力です。力の向きが万有引力のときと逆です。ですので k の前に - を付けます。つまり、

　　　　F = - k\(\large{\frac{(+1)\times q}{r^2}}\)

を r で積分します。万有引力による位置エネルギーを導き出したのと同じように計算します。＊これは点電荷のまわりの電場を r で積分するのと同じことです。この場合も正負を「万有引力」の話と合わせるために　E = \(k\large{\frac{q}{r^2}}\)　の右辺の k の前に - を付けてから積分します。
　閉じる

そうしますと、

　　　　U = k\(\large{\frac{q}{r}}\)　　（ r = ∞ のとき U = 0 ）

これが点電荷のまわりに置かれた +1 C の電荷の位置エネルギーであり、すなわち点電荷による電位です。つまり、

です。

いま、点電荷 q は正であるとしましたが、負であった場合は U も V も負になります＊ q が正、負、どちらの場合も距離 r が大きくなるにつれて（＝引力の場合でも斥力の場合でも離れれば離れるほど） U あるいは V は 0 に近づいていきます。
　閉じる。k の前に - を付けたりするわけではありません。右辺の q が正なら左辺の U や V も正で、右辺の q が負なら左辺の U や V も負です。（F の式に関しては、右辺の q が負のとき左辺の F は正です。引力ということです。ややこしいです。慣れが必要です。）

グラフ

これらのことを『万有引力による位置エネルギー』項にならってグラフで表してみます。

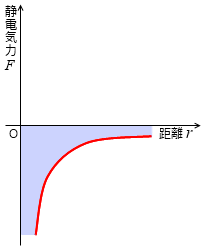電場の発生源の q が正のとき、+1 C の電荷との静電気力は左図における赤線であり、赤線と横軸で挟まれた部分の面積が位置エネルギーであり、電位です。

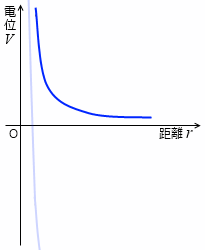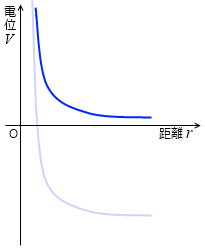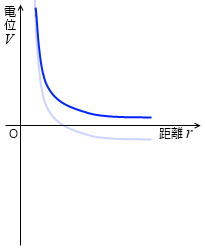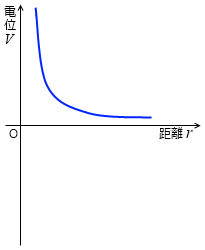青線が電位です。

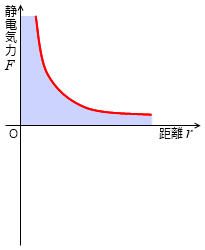電場の発生源の q が負のとき、+1 C の電荷との静電気力は左図における赤線であり、赤線と横軸で挟まれた部分の面積が位置エネルギーであり、電位です。

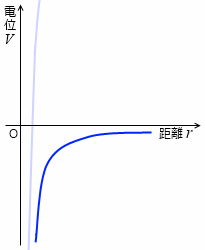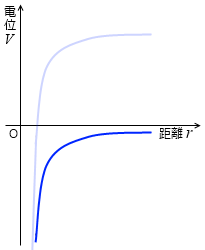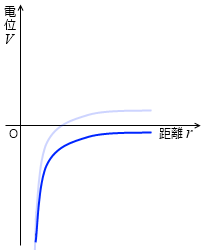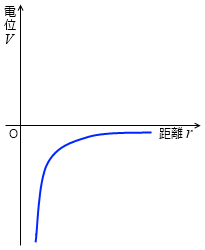青線が電位です。

たとえば正の点電荷が2つあったときは、電位を表すグラフは以下のようになります。

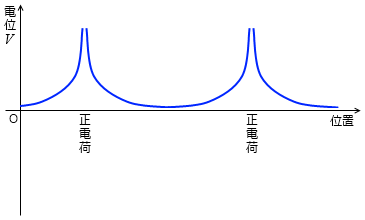
正の点電荷と負の点電荷がある場合であれば、電位を表すグラフは以下のようになります。

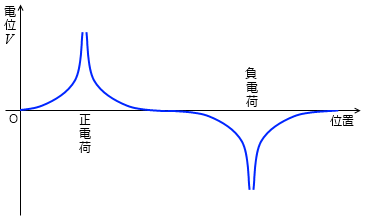
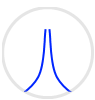山の先端部分はどうなっているかといいますと、それは無限に高くなっていて2つの曲線は極限まで近づくが接しない、ということになっています。