電流計⋅電圧計
電流計⋅電圧計の話は抵抗の話
本項では、電流計、電圧計について説明しますが、それらの装置の原理というよりも、電気回路に、どのような大きさの抵抗をどのように接続すれば、電流や電圧をうまく測定できるか、ということを解説します。
前提となる基本事項
本項の説明はかなり長くて複雑にみえますが、下記の基本事項からすべてを導くことができます。
直列接続
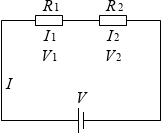 R1 の抵抗と R2 の抵抗を直列接続すると、
R1 の抵抗と R2 の抵抗を直列接続すると、
全体の抵抗 R は R = R1 + R2 であり、
電流に関しては I = I1 = I2 であり、
全体の電圧 V は V = V1 + V2 です。
並列接続
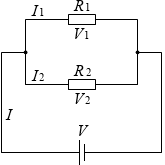 R1 の抵抗と R2 の抵抗を並列接続すると、
R1 の抵抗と R2 の抵抗を並列接続すると、
全体の抵抗 R は \(\large{\frac{1}{R}}\) = \(\large{\frac{1}{R_1}}\) + \(\large{\frac{1}{R_2}}\) であり、
全体の電流 I は I = I1 + I2 であり、
電圧に関しては V = V1 = V2 です。
オームの法則
オームの法則といったら V = RI です。
電流計
電流計の原理
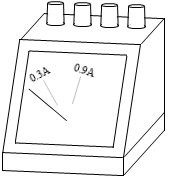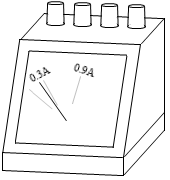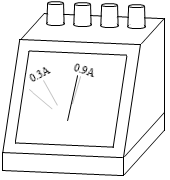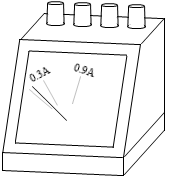 電流計は、電流が磁場から力を受ける現象を応用した計測器です。指針が取り付けられた回転軸は、電流が大きいほど大きな力を受け回転し、目盛盤には該当する電流の大きさが記されています。たとえば、0.3A の電流が流れたとき回転軸が 20°回転したとすると、0.9A の電流が流れたときは回転軸は 60°回転し、そのときの指針の位置の目盛盤には「0.9A」と記されています。
電流計は、電流が磁場から力を受ける現象を応用した計測器です。指針が取り付けられた回転軸は、電流が大きいほど大きな力を受け回転し、目盛盤には該当する電流の大きさが記されています。たとえば、0.3A の電流が流れたとき回転軸が 20°回転したとすると、0.9A の電流が流れたときは回転軸は 60°回転し、そのときの指針の位置の目盛盤には「0.9A」と記されています。
電流計は直列に接続して測定する
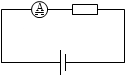 電流計は計りたい箇所に直列に接続します。電流計(直流電流計)の記号は
電流計は計りたい箇所に直列に接続します。電流計(直流電流計)の記号は 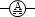 です。単に
です。単に 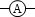 とすることもあります。
とすることもあります。
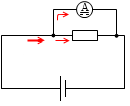 電流計を並列に接続してしまうと、電流は二股に分れてしまうので計りたい箇所の本当の電流を計測できません。
電流計を並列に接続してしまうと、電流は二股に分れてしまうので計りたい箇所の本当の電流を計測できません。
電流計の内部抵抗
電流計には内部抵抗があります。内部抵抗は測定値を狂わせます。
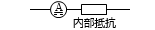 ここでは便宜上、この内部抵抗を電流計の外部にあるかのように図示します。
ここでは便宜上、この内部抵抗を電流計の外部にあるかのように図示します。
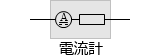 抵抗の記号と電流計の記号を合わせた全体が電流計であることとします。電池の内部抵抗の場合と一緒です。
抵抗の記号と電流計の記号を合わせた全体が電流計であることとします。電池の内部抵抗の場合と一緒です。
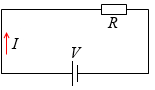 R [Ω] の抵抗が V [V] の電源につながれているとき、
R [Ω] の抵抗が V [V] の電源につながれているとき、
流れる電流 I はオームの法則より I = \(\large{\frac{V}{R}}\) [A] です。
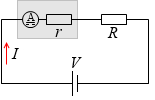 ところが、電流を計ろうとして電流計を接続すると電流計の内部抵抗により電流の大きさが変わってしまいます。電流計の内部抵抗を r [Ω] とすると電流の大きさは I = \(\large{\frac{V}{R+r}}\) [A] になってしまいます。
ところが、電流を計ろうとして電流計を接続すると電流計の内部抵抗により電流の大きさが変わってしまいます。電流計の内部抵抗を r [Ω] とすると電流の大きさは I = \(\large{\frac{V}{R+r}}\) [A] になってしまいます。
r の分だけ電流が小さくなってしまいます。電流計のジレンマです*このようなジレンマは他にもあります。
温度を計りたいときに、検査対象物に温度計を差し込むと温度計自体の温度によって検査対象物の温度を狂わせてしまいます。ですので、正確に計りたいときは、温度計を差し込む前に予想される温度付近に温度計を温める(あるいは冷やす)必要があります。
レントゲン撮影もジレンマを抱えています。病気を発見するためにレントゲン撮影は欠かせませんが、レントゲン撮影自体によって人は被曝し健康を害します。(被曝覚悟でもっと強い線量を当てると、もっと鮮明な画像が得られる、らしいです。)
『ホイートストンブリッジと電位差計』もご参照ください。
閉じる。
このジレンマをちょっとでも解消するために、電流計の内部抵抗はなるべく小さくすべきです。
電流計の最大測定範囲の拡大
電流計は、最大測定範囲を簡単に拡大することができます。50mA までしか計れない電流計を、簡単に 500mA あるいは 5A まで計れるようにすることができます。
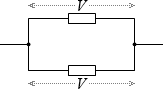 並列接続された部分は抵抗の大きさにかかわらず電圧が同じで、
並列接続された部分は抵抗の大きさにかかわらず電圧が同じで、
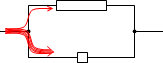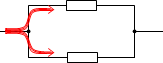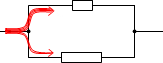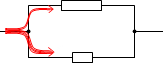 電流の大きさは抵抗の大きさに反比例する、という性質を利用します。
電流の大きさは抵抗の大きさに反比例する、という性質を利用します。
(50mA → 500mA の例)
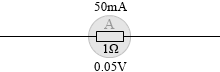 50mA までしか計れない、それ以上の電流が流れると壊れてしまう電流計があるとします。この電流計の内部抵抗が 1Ω であるとします。この部分に 0.05V の電圧を掛けます。つまり今、(0.05V÷1Ω=) 50mA の限度ぎりぎりの電流が流れているわけです。
50mA までしか計れない、それ以上の電流が流れると壊れてしまう電流計があるとします。この電流計の内部抵抗が 1Ω であるとします。この部分に 0.05V の電圧を掛けます。つまり今、(0.05V÷1Ω=) 50mA の限度ぎりぎりの電流が流れているわけです。
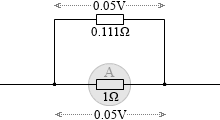 この回路を二股に分流し、0.111Ω の抵抗をつなげます。すると、この部分にも 0.05V の電圧が掛かるので (0.05V÷0.111Ω=0.05÷(1/9)=0.05×9=) 450mA の電流が流れます。
この回路を二股に分流し、0.111Ω の抵抗をつなげます。すると、この部分にも 0.05V の電圧が掛かるので (0.05V÷0.111Ω=0.05÷(1/9)=0.05×9=) 450mA の電流が流れます。
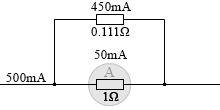 すると合計で (50mA+450mA=) 500mA の電流が流れていることになります。分流したおかげで 50mA の 10倍の電流を流すことができたのです。
すると合計で (50mA+450mA=) 500mA の電流が流れていることになります。分流したおかげで 50mA の 10倍の電流を流すことができたのです。
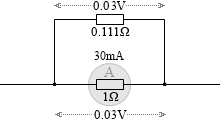 もしこのとき、電流計の値が 30mA の値(限度の 60%)を示していれば、この部分には (1Ω×0.03A=) 0.03V の電圧が掛かっていることになり、分流した部分にも 0.03V の電圧が掛かっていて、その部分の抵抗が 0.111Ω なのだから、(0.03V÷0.111Ω=0.03×9=) 270mA の電流が流れていることになります。
もしこのとき、電流計の値が 30mA の値(限度の 60%)を示していれば、この部分には (1Ω×0.03A=) 0.03V の電圧が掛かっていることになり、分流した部分にも 0.03V の電圧が掛かっていて、その部分の抵抗が 0.111Ω なのだから、(0.03V÷0.111Ω=0.03×9=) 270mA の電流が流れていることになります。
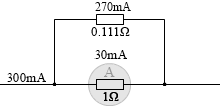 すると全体で (30mA+270mA=) 300mA の電流が流れていると分かります。電流計が 30mA の値を示しているときはその 10倍の電流が流れていることを意味しているわけです。
すると全体で (30mA+270mA=) 300mA の電流が流れていると分かります。電流計が 30mA の値を示しているときはその 10倍の電流が流れていることを意味しているわけです。
(50mA → 5A の例)
今度は、同じ 50mA 電流計(内部抵抗 1Ω)で 100倍の 5A までの電流を測定する方法を示します。
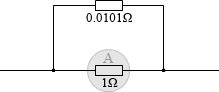 それは、分流した部分に 0.0101Ω の抵抗をつなげる、というものです。
それは、分流した部分に 0.0101Ω の抵抗をつなげる、というものです。
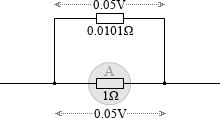 電流計の部分に 0.05V の電圧が掛かっているとします。流れる電流は (0.05V÷1Ω=) 50mA です。
電流計の部分に 0.05V の電圧が掛かっているとします。流れる電流は (0.05V÷1Ω=) 50mA です。
分流した部分にも 0.05V の電圧が掛かかっています。このとき電流は (0.05V÷0.0101Ω=0.05÷(1/99)=0.05×99=) 4.95A です。
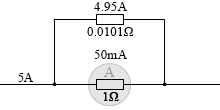 すると合計で (50mA+4.95A=) 5A の電流が流れていることになります。分流したおかげで 50mA の 100倍の電流を流すことができたのです。
すると合計で (50mA+4.95A=) 5A の電流が流れていることになります。分流したおかげで 50mA の 100倍の電流を流すことができたのです。
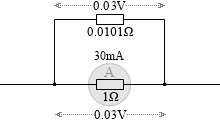 もしこのとき、電流計の値が 30mA の値(限度の 60%)を示していれば、この部分には (1Ω×0.03A=) 0.03V の電圧が掛かっていることになり、分流した部分にも 0.03V の電圧が掛かっていて、その部分の抵抗が 0.0101Ω なのだから、(0.03V÷0.0101Ω=0.03×99=) 2.97A の電流が流れていることになります。
もしこのとき、電流計の値が 30mA の値(限度の 60%)を示していれば、この部分には (1Ω×0.03A=) 0.03V の電圧が掛かっていることになり、分流した部分にも 0.03V の電圧が掛かっていて、その部分の抵抗が 0.0101Ω なのだから、(0.03V÷0.0101Ω=0.03×99=) 2.97A の電流が流れていることになります。
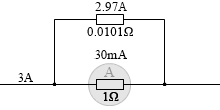 すると全体で (30mA+2.97A=) 3A の電流が流れていると分かります。電流計が 30mA の値を指し示しているときはその 100倍の電流が流れていることを意味しているわけです。
すると全体で (30mA+2.97A=) 3A の電流が流れていると分かります。電流計が 30mA の値を指し示しているときはその 100倍の電流が流れていることを意味しているわけです。
(50mA → 50A では?)
するどい方は、最大測定範囲を 1000倍にしたいときは 0.001001Ω の抵抗を並列に接続すればいい、とお察しになるかと思います。
このように、電流計の最大測定範囲を変更したい場合は、抵抗を並列に接続して電流を分流してやればいいのです。そのときの抵抗の大きさは、10倍にしたいときは 0.111Ω、100倍にしたいときは 0.0101Ω、1000倍にしたいときは 0.001001Ω にします。*厳密にはそれぞれ 0.11111…Ω 、0.01010101…Ω 、0.001001001001…Ω です。
閉じる
0.111 というのは \(\large{\frac{1}{9}}\) のことで、
0.0101 というのは \(\large{\frac{1}{99}}\) のことで、
0.001001 というのは \(\large{\frac{1}{999}}\) のことです。
つまり、
10倍にしたいときは \(\large{\frac{1}{10-1}}\) 倍の抵抗を、
100倍にしたいときは \(\large{\frac{1}{100-1}}\) 倍の抵抗を、
1000倍にしたいときは \(\large{\frac{1}{1000-1}}\) 倍の抵抗を並列に接続すればいいわけです。
このような抵抗を並列に接続すれば、そちらに 10-1倍、100-1倍、1000-1倍の電流が流れ、全体では 10倍、100倍、1000倍の電流が流れます。
電流計の最大測定範囲を拡大するための抵抗を分流器といい、元の電流計の内部抵抗を rA [Ω] 、分流器の抵抗を RA [Ω] 、拡大する倍率を n とすると、
分流器
RA = \(\large{\frac{r_A}{n-1}}\)
という関係になります。n は 10のべき乗だけというわけではありません。上の例でたまたま 10のべき乗の場合を示しただけです。
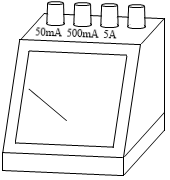 一般の電流計は、上部の複数の接続部に「50mA」「500mA」「5A」などと記されていますが、これは電流計の内部に分流器が内蔵されていて、分流器をつなぎ変えることによって最大測定範囲を変更できる、というものです。
一般の電流計は、上部の複数の接続部に「50mA」「500mA」「5A」などと記されていますが、これは電流計の内部に分流器が内蔵されていて、分流器をつなぎ変えることによって最大測定範囲を変更できる、というものです。
電圧計
電圧計の原理
電圧計は電流計を改造したものです。電流計の内部抵抗を大きくして(理由は以下で説明します)、目盛盤を入れ替えると電圧計になります。
内部抵抗が 100Ω の電流計に 10mA の電流を流したとき、指針の付いた回転軸が 20°回転したとします。この電流計に 30mA の電流を流せば回転軸は 60°回転します。
このときの電圧は、10mA の電流を流したときは (100Ω×0.01A=) 1V 、30mA の電流を流したときは (100Ω×0.03A=) 3V です。
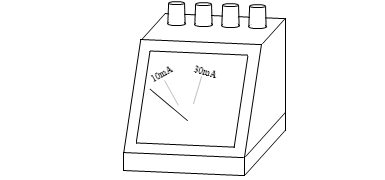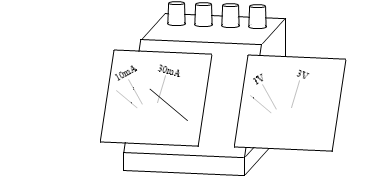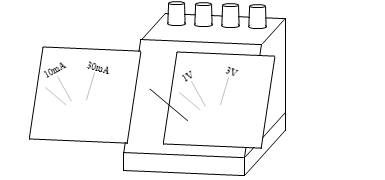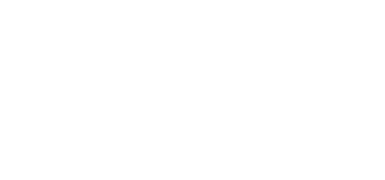 ですから、回転軸が 20°回転したときに指針が指し示す位置に「1V」、60°回転した位置に「3V」と記された目盛盤に入れ替えれば、これは電圧を測定する機器、となります。
ですから、回転軸が 20°回転したときに指針が指し示す位置に「1V」、60°回転した位置に「3V」と記された目盛盤に入れ替えれば、これは電圧を測定する機器、となります。
極端な言い方をすると、電圧計というものは所詮、電流を測定する機器です。といいますか、測定器にとって電流と電圧は同じものです。電圧の値は電流の値に内部抵抗の値を掛けただけのものです(オームの法則)。測定中は内部抵抗は変化せず固定されているので、電圧と電流は単純な比例関係にあります。
電圧計は並列に接続して測定する
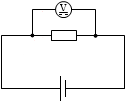 電圧計は計りたい箇所に並列に接続します。電圧計(直流電圧計)の記号は
電圧計は計りたい箇所に並列に接続します。電圧計(直流電圧計)の記号は 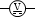 です。単に
です。単に 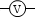 とすることもあります。
とすることもあります。
上で「電圧計は電流計である」と説明し、さらに上の方で「電流計は直列に接続する」と説明しましたので、電圧計も直列に接続すべきと感じてしまうかもしれませんが、そうではありません。
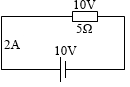 10V の電源に 5Ωの抵抗がつながれた回路があるとします。このとき流れる電流は (10V÷5Ω=) 2A です。
10V の電源に 5Ωの抵抗がつながれた回路があるとします。このとき流れる電流は (10V÷5Ω=) 2A です。
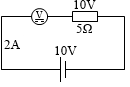 左図のように直列に電圧計をつなげたとします。でもこのとき測定できるのは電圧計自体にかかる電圧です。5Ω の抵抗部分の電圧は測定できていません。
左図のように直列に電圧計をつなげたとします。でもこのとき測定できるのは電圧計自体にかかる電圧です。5Ω の抵抗部分の電圧は測定できていません。
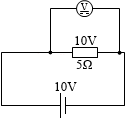 並列に電圧計をつなげたとします。すると、(上の方で説明しましたが)電流が二股に分かれるので本来の電流は測定できず、電圧計の構造は電流計の構造と同じもののはずだから、本来の値が測定できない、と感じてしまうかもしれません。
並列に電圧計をつなげたとします。すると、(上の方で説明しましたが)電流が二股に分かれるので本来の電流は測定できず、電圧計の構造は電流計の構造と同じもののはずだから、本来の値が測定できない、と感じてしまうかもしれません。
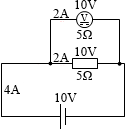 しかし、電圧計の内部抵抗を 5Ω *これは別に、下の 5Ω の抵抗に合わせたわけではありません。話の例です。何Ωでもかまいません。
しかし、電圧計の内部抵抗を 5Ω *これは別に、下の 5Ω の抵抗に合わせたわけではありません。話の例です。何Ωでもかまいません。
閉じるとしますと全体の抵抗は 2.5Ω *\(\large{\frac{1}{x}}\) = \(\large{\frac{1}{5Ω}}\) + \(\large{\frac{1}{5Ω}}\) を解くと x = 2.5Ω です。
暗算で、「5Ωの抵抗が2つ並行に合わさって、抵抗の大きさが半分になるから 2.5Ω」と考えてもいいです。
閉じるになり、回路に流れる電流は (10V÷2.5Ω=) 4A となります。それが均等に二股に分かれているので電圧計に流れる電流は 2A となり、内部抵抗が 5Ω ですから電圧は (5Ω×2A=) 10V となり、正しく計測できます。計測値が半分の 5V になってしまうなどということは起こりません。
二股に分かれると電流が減ってしまうと思いきや、元々の電流が増えるのでトータルで大丈夫なのです。
電圧を計るときは「並列」接続です。
電圧計の内部抵抗
電流計と同じように電圧計にも内部抵抗があります。この内部抵抗は大きい方がいいか、小さい方がいいか、考えてみます。
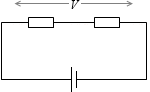 左図のように回路全体の電圧を計るときは何も問題無いのですが、
左図のように回路全体の電圧を計るときは何も問題無いのですが、
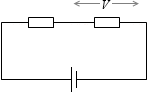 左図のように一部分の電圧を計るときは電圧計の内部抵抗が問題になります。
左図のように一部分の電圧を計るときは電圧計の内部抵抗が問題になります。
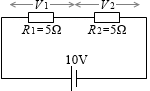 電源の電圧を 10V 、R1 の抵抗を 5Ω 、R2 の抵抗を 5Ω 、R1 に掛かる電圧を V1 、R2 に掛かる電圧を V2 とします。
電源の電圧を 10V 、R1 の抵抗を 5Ω 、R2 の抵抗を 5Ω 、R1 に掛かる電圧を V1 、R2 に掛かる電圧を V2 とします。
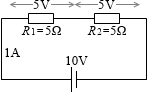 すると、全体の抵抗は 10Ω であり、電流は 1A であり、V1 = 5V 、V2 = 5V であります。
すると、全体の抵抗は 10Ω であり、電流は 1A であり、V1 = 5V 、V2 = 5V であります。
この 5V を正確に読み取るにはどうしたらいいか考えます。
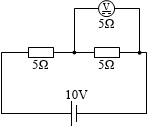 R2 に掛かる電圧を計ろうとして内部抵抗 5Ω の電圧計を並列につなげたとします。
R2 に掛かる電圧を計ろうとして内部抵抗 5Ω の電圧計を並列につなげたとします。
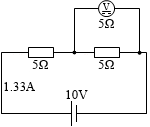 すると、R2 の抵抗と電圧計の内部抵抗とを合わせた合成抵抗は(上の方で説明しましたが)2.5Ω になります。R1 の抵抗は 5Ω なので、回路全体の抵抗は 7.5Ω です。そして、電源が 10V なので回路を流れる電流は (10V÷7.5Ω=) 1.33A です。
すると、R2 の抵抗と電圧計の内部抵抗とを合わせた合成抵抗は(上の方で説明しましたが)2.5Ω になります。R1 の抵抗は 5Ω なので、回路全体の抵抗は 7.5Ω です。そして、電源が 10V なので回路を流れる電流は (10V÷7.5Ω=) 1.33A です。
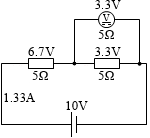 すると、電圧 V1 は (5Ω×1.33A≒) 6.7V 、電圧 V2 は (2.5Ω×1.33A≒) 3.3V となり*電圧計を流れる電流と抵抗R2を流れる電流との合計が 1.33A です。電圧計を流れる電流はその半分の 0.67A で、抵抗R2を流れる電流も 0.67A です。
すると、電圧 V1 は (5Ω×1.33A≒) 6.7V 、電圧 V2 は (2.5Ω×1.33A≒) 3.3V となり*電圧計を流れる電流と抵抗R2を流れる電流との合計が 1.33A です。電圧計を流れる電流はその半分の 0.67A で、抵抗R2を流れる電流も 0.67A です。
電圧計の内部抵抗と抵抗R2の抵抗との合成抵抗の値は 2.5Ω です。
閉じる、本来の V1 = 5V 、V2 = 5V ではなくなってしまいます。電圧を正確に計れていません。電圧計のジレンマです。電圧計をつなげたことによって V1 と V2 のバランスが崩れたのです。電圧のバランスは抵抗のバランスです。抵抗のバランスが崩れると電圧が正確に測定できなくなるのです。
このことを避けるためには電圧計の内部抵抗をできるだけ大きくする必要があります。電圧計の内部抵抗が大きければ、R2 と内部抵抗との合成抵抗が、R2 とあまり変わらず*電圧計の内部抵抗が大きいと、合成抵抗が R2 とあまり変わらない、ということを数式を使って説明します。
電圧計の内部抵抗を RV とし、R2 と RV との合成抵抗を RX とします。
\(\large{\frac{1}{R_x}}\) = \(\large{\frac{1}{R_2}}\) + \(\large{\frac{1}{R_V}}\) であるから、
RX = \(\large{\frac{R_2 R_V}{R_2+R_V}}\)
もし、R2 ≪ RV ならば、
\(\large{\frac{R_2 R_V}{R_2+R_V}}\) ≒ \(\large{\frac{R_2 R_V}{0+R_V}}\) = \(\large{\frac{R_2 R_V}{R_V}}\) = R2
であるので、R2 ≪ RV ならば RX ≒ R2
ということがいえます。
閉じる、R1 と R2 のバランスが変わらず、V1 と V2 とのバランスも変わらず、正確に測定することができます。
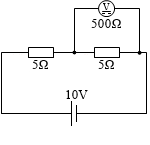 上の例に当てはめますと、電圧計の内部抵抗が 500Ω であった場合、電圧計の内部抵抗と R2 との合成抵抗 RX は、
上の例に当てはめますと、電圧計の内部抵抗が 500Ω であった場合、電圧計の内部抵抗と R2 との合成抵抗 RX は、
\(\large{\frac{1}{R_x}}\) = \(\large{\frac{1}{5Ω}}\) + \(\large{\frac{1}{500Ω}}\) であるから、
\(\large{\frac{1}{R_x}}\) = \(\large{\frac{100}{500}}\) + \(\large{\frac{1}{500}}\) = \(\large{\frac{101}{500}}\) であり、
RX ≒ 5Ω となり、この値は R2 の値とほぼ同じです。
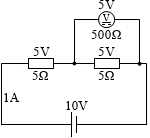 全体の抵抗は (5Ω+5Ω=) 10Ω であり、回路を流れる電流は (10V÷10Ω=) 1A であり、V1 は (5Ω×1A=) 5V であり、V2 も (5Ω×1A=) 5V であり、ほぼ正確に測定できていることになります。
全体の抵抗は (5Ω+5Ω=) 10Ω であり、回路を流れる電流は (10V÷10Ω=) 1A であり、V1 は (5Ω×1A=) 5V であり、V2 も (5Ω×1A=) 5V であり、ほぼ正確に測定できていることになります。
内部抵抗がもっと大きければさらに正確に測定できます。
つまり、電圧計の内部抵抗はなるべく大きくすべきです。
電圧計の最大測定範囲の拡大
電圧計も電流計と同様、最大測定範囲を簡単に拡大することができます。3V までしか計れない電圧計を簡単に 30V あるいは 300V まで計れるようにすることができます。
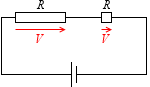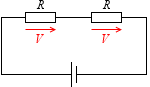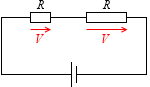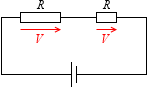 直列接続された部分の電圧の大きさは抵抗の大きさに比例する、という性質を利用します。
直列接続された部分の電圧の大きさは抵抗の大きさに比例する、という性質を利用します。
(3V → 30V の例)
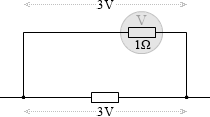 3V までしか計れない、それ以上の電圧を掛けると壊れてしまう電圧計があるとします。この電圧計の内部抵抗が 1Ω であるとします。この電圧計に限度ぎりぎりの 3V の電圧を掛けます。流れる電流は (3V÷1Ω=) 3A です。
3V までしか計れない、それ以上の電圧を掛けると壊れてしまう電圧計があるとします。この電圧計の内部抵抗が 1Ω であるとします。この電圧計に限度ぎりぎりの 3V の電圧を掛けます。流れる電流は (3V÷1Ω=) 3A です。
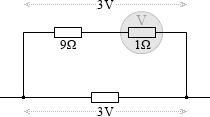 この電圧計に直列に 9Ω の抵抗をつなげます。そして、電圧計とこの抵抗を合わせた全体の部分に掛ける電圧は 3V のままとします。
この電圧計に直列に 9Ω の抵抗をつなげます。そして、電圧計とこの抵抗を合わせた全体の部分に掛ける電圧は 3V のままとします。
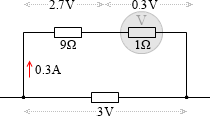 すると合計の抵抗は (9Ω+1Ω=) 10Ω です。掛ける電圧は 3V のままなので電流は (3V÷10Ω=) 0.3A です。ですので、抵抗に掛かる電圧は (9Ω×0.3A=) 2.7V で、電圧計に掛かる電圧は (1Ω×0.3A=) 0.3V です。最初、電圧計に 3V の電圧が掛かっていましたが、9Ω の抵抗を直列につなげたことによって、0.3V に下がったわけです。
すると合計の抵抗は (9Ω+1Ω=) 10Ω です。掛ける電圧は 3V のままなので電流は (3V÷10Ω=) 0.3A です。ですので、抵抗に掛かる電圧は (9Ω×0.3A=) 2.7V で、電圧計に掛かる電圧は (1Ω×0.3A=) 0.3V です。最初、電圧計に 3V の電圧が掛かっていましたが、9Ω の抵抗を直列につなげたことによって、0.3V に下がったわけです。
9Ω の抵抗を付け足したおかげで電圧計の電圧が \(\large{\frac{1}{10}}\) に下がったのです。これであれば以前の 10倍の電圧を掛けることができます。
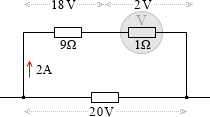 もしこのとき全体の電圧が不明の場合で、電圧計の値が 2V(限度の 67%)を指し示していたとします。すると、電圧計の内部抵抗は 1Ω だから電圧計に流れる電流は (2V÷1Ω=) 2A です。抵抗にも同じ値の電流が流れているはずだから、抵抗の電圧は (9Ω×2A=) 18V です。 全体の電圧は (18V+2V=) 20V です。電圧計の指し示す値の 10倍です。
もしこのとき全体の電圧が不明の場合で、電圧計の値が 2V(限度の 67%)を指し示していたとします。すると、電圧計の内部抵抗は 1Ω だから電圧計に流れる電流は (2V÷1Ω=) 2A です。抵抗にも同じ値の電流が流れているはずだから、抵抗の電圧は (9Ω×2A=) 18V です。 全体の電圧は (18V+2V=) 20V です。電圧計の指し示す値の 10倍です。
(3V → 300V の例)
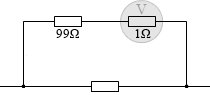 同様に考えますと、100倍の電圧に耐えられるようにするためには、直列に接続する抵抗の値を 99Ω にすればいいと分かります。
同様に考えますと、100倍の電圧に耐えられるようにするためには、直列に接続する抵抗の値を 99Ω にすればいいと分かります。
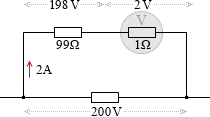 このとき電圧計の値が 2V を指し示していたとすると、電圧計の内部抵抗は 1Ωだから電圧計に流れる電流は (2V÷1Ω=) 2A で、抵抗にも同じ値の電流が流れるから、抵抗の電圧は (99Ω×2A=) 198V です。全体の電圧は (198V+2V=) 200V です。電圧計の指し示す値の 100倍です。
このとき電圧計の値が 2V を指し示していたとすると、電圧計の内部抵抗は 1Ωだから電圧計に流れる電流は (2V÷1Ω=) 2A で、抵抗にも同じ値の電流が流れるから、抵抗の電圧は (99Ω×2A=) 198V です。全体の電圧は (198V+2V=) 200V です。電圧計の指し示す値の 100倍です。
このように、電圧計の最大測定範囲を変更したい場合は、抵抗を直列に接続すればいいのです。そのときの抵抗の大きさは、
10倍にしたいときは内部抵抗の 10-1倍、
100倍にしたいときは内部抵抗の 100-1倍、
1000倍にしたいときは内部抵抗の 1000-1倍です。
このような抵抗を直列に接続すれば、そちらに 10-1倍、100-1倍、1000-1倍の電圧が掛かり、全体では 10倍、100倍、1000倍の電圧が掛かります。
電圧計の最大測定範囲を拡大するための抵抗を倍率器といい、元の電圧計の内部抵抗を rV [Ω] 、倍率器の抵抗を RV [Ω] 、拡大する倍率を n とすると、
倍率器
RV = (n-1) rV
という関係になります。n は 10のべき乗というわけではありません。上の例でたまたま 10のべき乗の場合を示しただけです。
一般の電圧計には倍率器が内蔵されていて、様々な大きさの電圧に対応できるようになっています。
電流計のために並列に接続した抵抗が「分流器」で、電圧計のために直列に接続した抵抗が「倍率器」です。