コンデンサーを流れる交流

コイルとコンデンサーと交流

『コイルを流れる交流』項で、コイルに交流を流した場合について説明しましたが、本項ではコンデンサーに交流を流した場合について説明します。『コイルを流れる交流』項と同じように説明していきます。

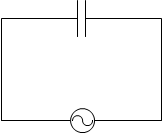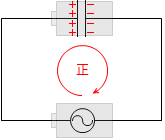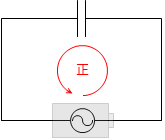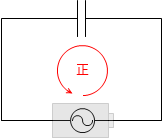
交流電源とコンデンサーを接続した回路

『コイルを流れる交流』項で、交流電源とコイルを接続した回路においては、電流の位相が電圧に比べて遅れる、と説明しましたが、交流電源とコンデンサーを接続した回路においては逆になります。電流の位相は電圧に比べて早くなります。タイミングが早くなるということです。

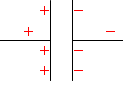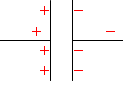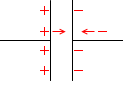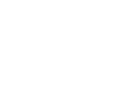不思議に思われるかもしれませんが、これはコンデンサーの極板間で電荷同士が引き合うためです。電荷が増えやすいのです。

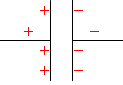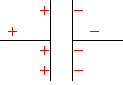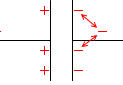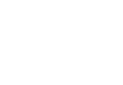逆に電荷が減っていく局面では、反対側の極板内で電荷同士の斥力がはたらき、電荷が減りやすくなります。

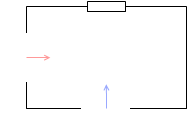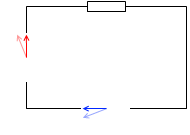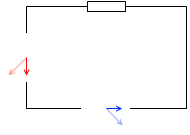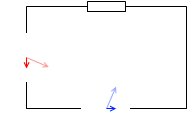抵抗器を接続した場合（電流の位相は電圧と同じ）や、

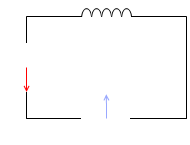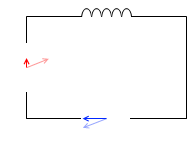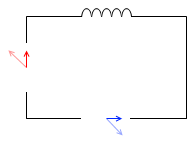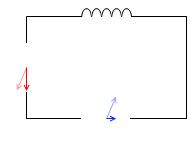コイルを接続した場合（電流の位相は電圧より遅れる）に比べて、

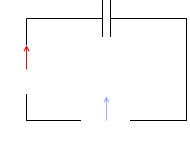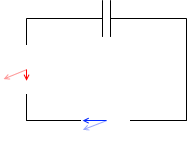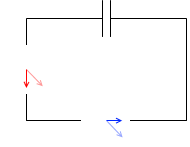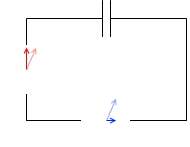コンデンサーを接続した場合は、電流の変化のタイミングが早くなります（電流の位相は電圧より進む）。

電流を表す式を求める

交流電源の電圧を V = V₀sinωt [V]（V₀ は最大値）、回路を流れる電流を I [A] 、コンデンサーの電気容量を C [F] 、コンデンサーに蓄えられる電荷（電気量）を Q [C] 、コンデンサーに発生する電圧を V_C [V] とします。＊C と [C] を混同しないでください。C は電気容量を表す量記号、[C] は電荷（電気量）の単位です。
　閉じる

そうしますと、Q = CV_C だから、

　　　　V_C = \(\large{\frac{Q}{C}}\)

となるのですが、

回路において、交流電源の電圧の方向を正としますと、コンデンサーに蓄えられた電荷たちが作る起電力の向きは常に逆向きです。コンデンサーや電源を電池にたとえると、２つの電池は常に向き合っています。

ですので向きも含めて考えると、

　　　　V_C = - \(\large{\frac{Q}{C}}\)

となります。そして、回路に電流が流れる＊直流電源につながれたコンデンサーは時間が経つと満充電になり、電流がストップしますが、交流電源につながれたコンデンサーにおいては電流の向きが絶えず変わるので電流が流れ続けることになります。
　閉じるということは一周して戻ってくると電位が元通りになる（キルヒホッフ第2法則のこと）ということですから、

　　　　V + V_C = 0

　　⇒　V - \(\large{\frac{Q}{C}}\) = 0

　　∴　　　Q = CV

です。一方、電流というのは電荷を時間で割ったものであるので、 I = \(\large{\frac{Q}{t}}\) であるわけですが、これは電流の平均の値＊たとえば、10秒間に 30 C だけ電荷が増えたら、10秒間の電流の平均の大きさが 3 A 。
距離を時間で割って平均の速さを導き出すのと同じようなことです。
　閉じるのことであって、電流の瞬間の値は、

　　　　I = \(\large{\frac{ΔQ}{Δt}}\)

です。この式に Q = CV を代入すると、

　　　　I = \(\large{\frac{ΔCV}{Δt}}\)　　　電気容量 C は定数だから

　　　　　= C\(\large{\frac{ΔV}{Δt}}\)

V = V₀sinωt を代入すると、

　　　　I = C\(\large{\frac{ΔV_0\sinωt}{Δt}}\)　　　V₀ は定数だから

　　　　　= CV₀\(\large{\frac{Δ\sinωt}{Δt}}\)　　　sinωt の微分は ωcosωt だから

　　　　　= CV₀ ωcosωt

　　　　　= ωCV₀cosωt

この式と、電圧の式 V = V₀sinωt を見比べるため、cos のところを sin の形に変形してみます。三角関数の公式 cosα = sin\(\bigl(\)α + \(\large{\frac{π}{2}}\)\(\bigr)\) を用いますと、

　　　　I = ωCV₀sin\(\bigl(\)ωt + \(\large{\frac{π}{2}}\)\(\bigr)\)

となり、これを電圧の式

　　　　V = V₀sinωt

と見比べますと、電流の式の方は sin の中身に +\(\large{\frac{π}{2}}\) が付いていますので、位相が \(\large{\frac{π}{2}}\) 進んでいると分かります。

また、この式から電流 I の最大値も分かります。sinx の最大値は 1 であり、最小値は -1 です。x がどんな値であろうとも -1 ≦ sinx ≦ 1 です。つまり、上式の最大値は ωCV₀ です。これを I₀ とおきます。すなわち、I₀ = ωCV₀ であり変形しますと V₀ = \(\large{\frac{I_0}{ωC}}\) です。

ここまでのまとめ

コンデンサーを流れる交流は、電圧の位相より電流の位相の方が \(\large{\frac{π}{2}}\) 進みます。

これは別の表現をすると、電圧の位相の方が電流の位相より \(\large{\frac{π}{2}}\) 遅れている、ということになり、このことを式で表現すると、

　　　　V = V₀sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\)

　　　　I = ωCV₀sinωt

となります。

３番目の式の V₀ = \(\large{\frac{I_0}{ωC}}\) は電圧の最大値と電流の最大値の関係を表したものですが、実効値というものが最大値を単純に \(\large{\frac{1}{\sqrt{2}\ }}\) 倍したものであることから、V_e = \(\large{\frac{I_\rm{e}}{ωC}}\) という関係も成り立っています。

（コイルの場合と見比べてみてください。）

コンデンサーのリアクタンス

V₀ = \(\large{\frac{I_0}{ωC}}\)　式の　\(\large{\frac{1}{ωC}}\)　は、コイルのリアクタンスと同じように、電圧と電流の比率を決めるものです。これをコンデンサーのリアクタンス（容量性リアクタンス）といいます。量記号は X_C という文字を使います。単位は [Ω] です。

リアクタンスというものは『コイルのリアクタンス』で説明したように、電流の流れにくさを表すものであり、リアクタンスが大きいときほど電流は小さくなるのですが、X_C = \(\large{\frac{1}{ωC}}\) という式においてコンデンサーの電気容量を表す C が分母にきていますので、電気容量が大きいコンデンサーのときほどリアクタンスは小さくなり、電流は大きくなる、ということがいえます。

電気容量が大きいというのはたとえば極板が大きいということであり、このようなときは本項の一番上で示した引力や斥力がはたらきやすくなり、電流が大きくなる、ということです。

グラフ

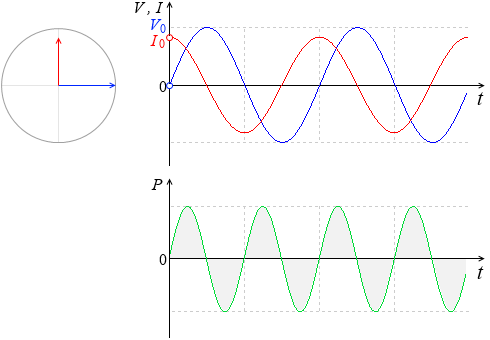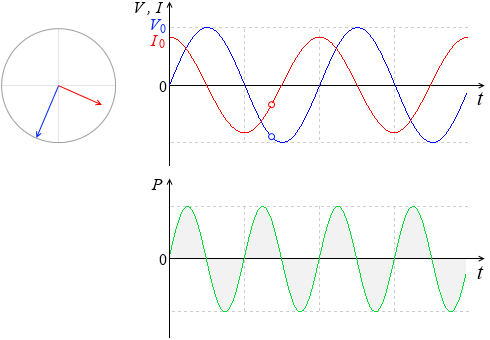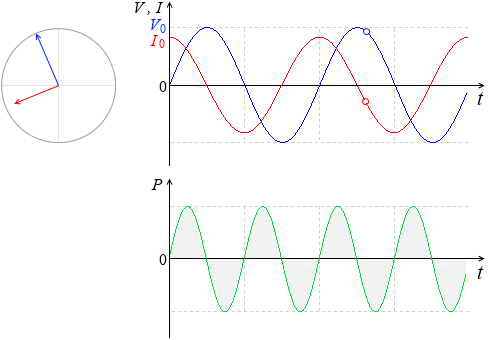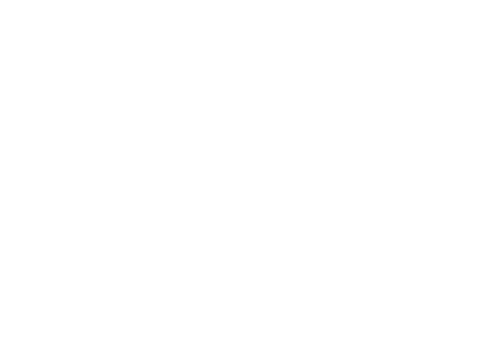『コイルを流れる交流』項の『グラフ』にならって、コンデンサーを流れる交流電圧

　　V = V₀sinωt

と交流電流

　　I = ωCV₀sin\(\bigl(\)ωt + \(\large{\frac{π}{2}}\)\(\bigr)\)

のグラフを描いてみます。

電流の方が位相が \(\large{\frac{π}{2}}\) 進んでいます。

下は電力のグラフです。

電力

『コイルを流れる交流』項の『電力』にならって、電力も求めてみます。

電流の式は I = ωCV₀sin\(\bigl(\)ωt + \(\large{\frac{π}{2}}\)\(\bigr)\) ですが、この式はもともと変形前は、

　　　　I = ωCV₀cosωt

でした。この式に V₀ = \(\large{\frac{I_0}{ωC}}\) を代入します。

　　　　I = I₀cosωt

この電流の式と、電圧の式 V = V₀sinωt を掛け合わせて電力 P の式を導き出します。

　　　　P = I × V

　　　　　= I₀cosωt × V₀sinωt

　　　　　= I₀V₀ cosωt × sinωt　　　　２倍角の公式　sin2θ = 2sinθcosθ　を適用します

　　　　　= I₀V₀\(\large{\frac{1}{2}}\) sin2ωt

　　　　　= \(\large{\frac{1}{2}}\)I₀V₀ sin2ωt

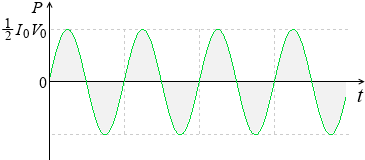これをグラフにしたものが上で示した電力のグラフです。最大値が \(\large{\frac{1}{2}}\)I₀V₀ であり、角速度が ω から 2ω に増えています。

この曲線は 0 を中心にして振動しているので、和をとる（時間平均をとる）とトータルで 0 になります。電力の総和が 0 、これはつまり、交流を流したコンデンサーでは電力が消費されない、ということです。ジュール熱が発生しないということです。＊『コイルを流れる交流』項の『電力』の最後の＊の中の解説をお読みください。
　閉じる

コイルの場合のグラフと比べると、違いは上下が反転していることだけです。