RLC直列回路

抵抗とコイルとコンデンサーを直列につなげる

交流電源と抵抗を接続した回路では、電流と電圧の位相は揃っています。
交流電源とコイルを接続した回路では、電流の位相は電圧より遅れます。
交流電源とコンデンサーを接続した回路では、電流の位相は電圧より進みます。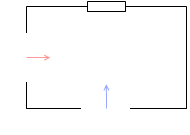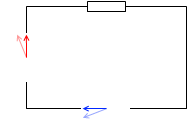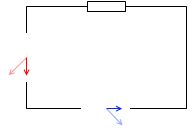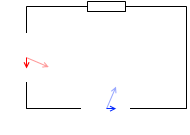＊ 抵抗器を接続した場合、電流の位相は電圧と同じ。
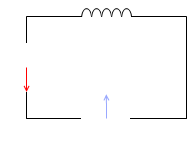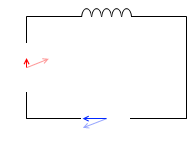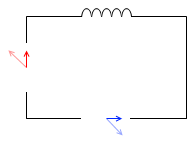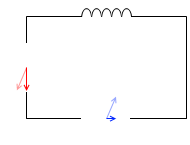コイルを接続した場合、電流の位相は電圧より遅れる。
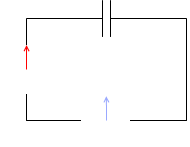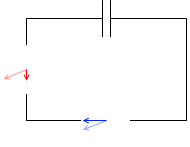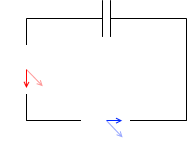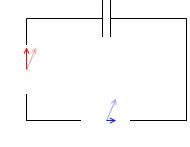コンデンサーを接続した場合、電流の位相は電圧より進む。
　閉じる

ではそれらを同時に、つまり抵抗とコイルとコンデンサーを直列に接続した場合どうなるか、考えてみます。

RLC直列回路

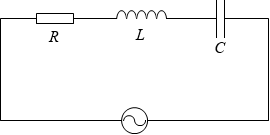電気抵抗 R [Ω] の抵抗、自己インダクタンス L [H] のコイル、電気容量 C [F] のコンデンサーを交流電源に直列に接続した回路について考えます。このような回路をRLC直列回路といいます。

（『共振回路』項の上から３番目のアニメーションもご参照ください。）

電流は同じで電圧は和

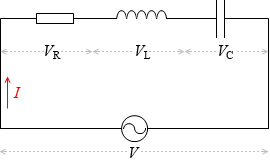直列接続ですから３つの装置に流れる電流は同じで、全体の電圧は３つの装置の各電圧の和です＊中学理科で習ったと思います。
並列接続の場合でしたら、電圧が同じで、電流が和、です。
キルヒホッフの法則のことです。
RLC直列回路以外にRLC並列回路というのもありますが、高校物理ではあまり取り上げられません。
　閉じる。電流を I = I₀sinωt [A]（I₀ は最大値）、交流電源の電圧を V [V] 、抵抗に掛かる電圧を V_R [V] 、コイルに掛かる電圧を V_L [V] 、コンデンサーに掛かる電圧を V_C [V] とします。

電圧 V_L の式

『コイルを流れる交流』項にならえば、コイルに流れる交流電圧と交流電流は、

　　　　V_L = V_L0sinωt　（V_L0 は最大値）

　　　　I = I₀sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\)　　　V_L0 = ωLI₀

と表せますが、その項の『ここまでのまとめ』のすぐ下で述べたのと同様、今は、

　　　　I = I₀sinωt

としてますので、それに合わせると電圧 V_L の式は、

　　　　V_L = V_L0sin\(\bigl(\)ωt + \(\large{\frac{π}{2}}\)\(\bigr)\)

ということになります。右辺に V_L0 = ωLI₀ を代入しますと、

　　　　V_L = ωLI₀sin\(\bigl(\)ωt + \(\large{\frac{π}{2}}\)\(\bigr)\)　　……①

です。

電圧 V_C の式

同様に、『コンデンサーを流れる交流』項にならうと、コンデンサーに流れる交流電圧と交流電流は、

　　　　V_C = V_C0sinωt　（V_C0 は最大値）

　　　　I = I₀sin\(\bigl(\)ωt + \(\large{\frac{π}{2}}\)\(\bigr)\)　　　V_C0 = \(\large{\frac{I_0}{ωC}}\)

と表せますが、その項の『ここまでのまとめ』のすぐ下で述べたのと同様、今は、

　　　　I = I₀sinωt

としてますので、それに合わせると電圧 V_C の式は、

　　　　V_C = V_C0sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\)

ということになります。右辺に V_C0 = \(\large{\frac{I_0}{ωC}}\) を代入しますと、

　　　　V_C = \(\large{\frac{I_0}{ωC}}\)sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\)　　……②

です。

電圧 V_R の式

抵抗を流れる交流電流を、

　　　　I = I₀sinωt

とした場合は単純にオームの法則より、 R を掛けて、

　　　　V_R = RI₀sinωt　　……③

となります。位相がズレるようなことはありません。

全体の電圧 V の式

③式、①式、②式を足し合わせて全体の電圧 V を求めてみます。

　　　　V = V_R + V_L + V_C

　　　　　= RI₀sinωt + ωLI₀sin\(\bigl(\)ωt + \(\large{\frac{π}{2}}\)\(\bigr)\) + \(\large{\frac{I_0}{ωC}}\)sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\)

　　　　　= I₀\(\Bigl\{\)Rsinωt + ωLsin\(\bigl(\)ωt + \(\large{\frac{π}{2}}\)\(\bigr)\) + \(\large{\frac{1}{ωC}}\)sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\)\(\Bigr\}\)　　　第2項に三角関数の公式 sin\(\bigl(\)α + \(\large{\frac{π}{2}}\)\(\bigr)\) = cosα を適用しますと、

　　　　　= I₀\(\Bigl\{\)Rsinωt + ωLcosωt + \(\large{\frac{1}{ωC}}\)sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\)\(\Bigr\}\)　　　第3項に sin\(\bigl(\)ωt - \(\large{\frac{π}{2}}\)\(\bigr)\) = - cosωt ＊ この式の導出方法は 『コイルを流れる交流』項の『電流を表す式を求める』の ＊ の中をご覧ください。
　閉じる を代入しますと、

　　　　　= I₀\(\Bigl\{\)Rsinωt + ωLcosωt - \(\large{\frac{1}{ωC}}\)cosωt\(\Bigr\}\)

　　　　　= I₀\(\Bigl\{\)Rsinωt + \(\bigl(\)ωL - \(\large{\frac{1}{ωC}}\)\(\bigr)\)cosωt\(\Bigr\}\)

ここで { } の部分に三角関数の合成公式

　　asinθ + bcosθ = \(\sqrt{a^2+b^2}\)sin(θ+α)　　ただし tanα = \(\large{\frac{b}{a}}\)

を適用しますと、

　　　　V = I₀\(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\) sin(ωt + φ)　　ただし　tanφ = \(\large{\frac{ωL-\large{\frac{1}{ωC}}}{R}}\)　　　……④

となります。

別解

グラフを使った求め方も紹介しておきます。各式のグラフを描いてみます。

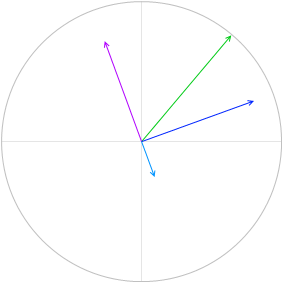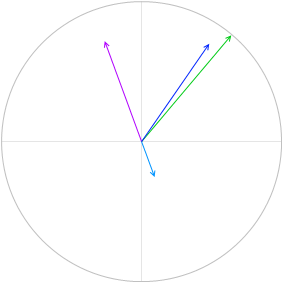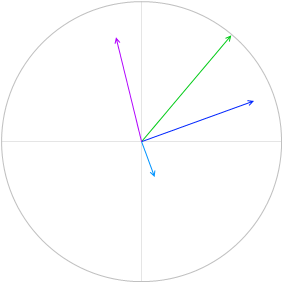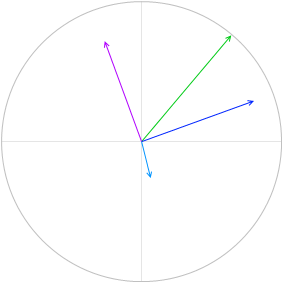
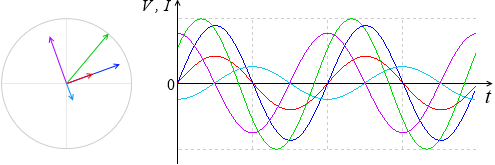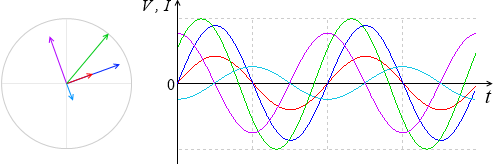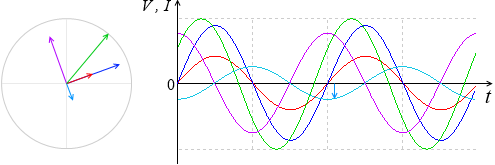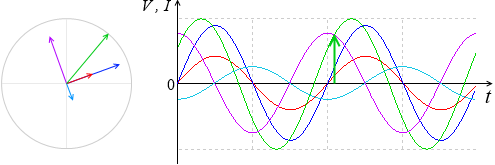V = V_R + V_L + V_C を求めるということは、曲線の各点の高さを足し合わせるということです。

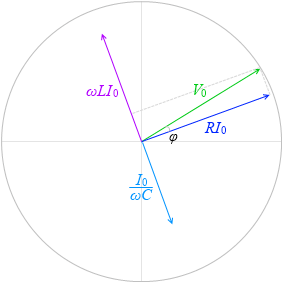
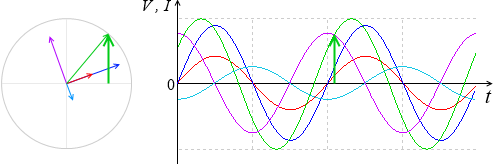この高さというのは合成ベクトル　\(\vec{\ V}\) = \(\vec{\ V_R}\) + \(\vec{\ V_L}\) + \(\vec{\ V_C}\)　の高さ（円グラフの y切片）のことです。

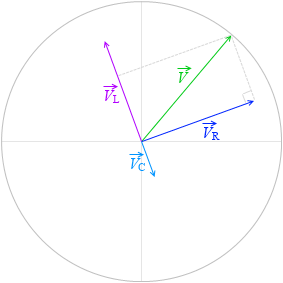まず三平方の定理を使って \(\vec{\ V}\) の長さ（高さではなく長さです）を求めます。

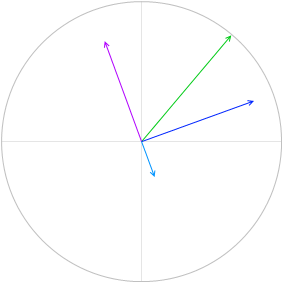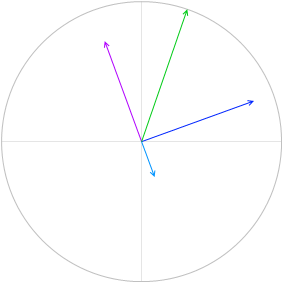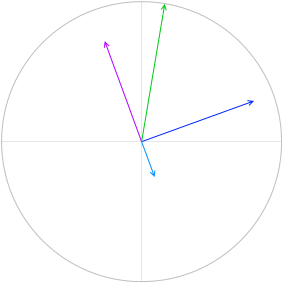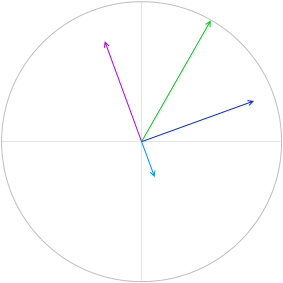\(\vec{\ V}\) の長さというのは V の最大値 V₀ のことです。

同様に、

\(\vec{\ V_R}\) の長さというのは V_R の最大値 RI₀ のこと、

\(\vec{\ V_L}\) の長さというのは V_L の最大値 ωLI₀ のこと、

\(\vec{\ V_C}\) の長さというのは V_C の最大値 \(\large{\frac{I_0}{ωC}}\) のことです。

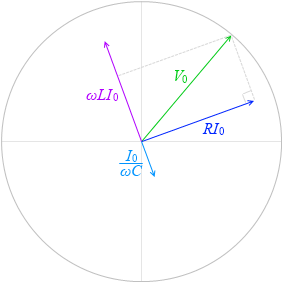三平方の定理より、

　　　　V₀² = (RI₀)² + \(\bigl(\)ωLI₀ - \(\large{\frac{I_0}{ωC}}\)\(\bigr)^2\)　　……⑤

　　　　　　= R²I₀² + \(\bigl(\)ωL - \(\large{\frac{1}{ωC}}\)\(\bigr)^2\) I₀²

　　　　　　= I₀² \(\Bigl\{\)R² + \(\bigl(\)ωL - \(\large{\frac{1}{ωC}}\)\(\bigr)^2\)\(\Bigr\}\)

　∴　　V₀ = I₀\(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\)　　……⑥

これが \(\vec{\ V}\) の長さです。

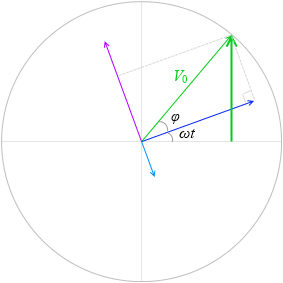これに sin(ωt + φ) を掛ければ \(\vec{\ V}\) の高さ V が求まります。

つまり、

　　　　V = I₀\(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\) sin(ωt + φ)

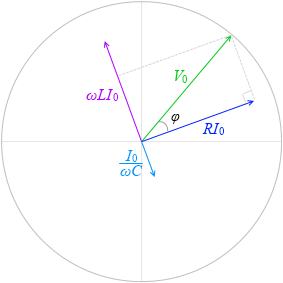φ の大きさは、

　　tanφ = \(\large{\frac{ωLI_0-\large{\frac{I_0}{ωC}}}{RI_0}}\) = \(\large{\frac{ωL-\large{\frac{1}{ωC}}}{R}}\)

であり、

④式と同じ結果が得られます。

インピーダンス

『コイルを流れる交流』項の『まとめ』における　V₀ = ωLI₀　式、
『コンデンサーを流れる交流』項の『まとめ』における　V₀ = \(\large{\frac{I_0}{ωC}}\)　式、に相当するのが上の⑥式

　　　　V₀ = I₀\(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\)

であり、\(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\) の部分はコイルのリアクタンスやコンデンサーのリアクタンスと同じように、電圧と電流の比率を決めるものであり、電流の流れにくさを表すものであります。これをインピーダンス＊impedance = impede（妨げる）+ ance（量・程度を表す名詞語尾）

量記号に Z を用いる理由は分かりません。
　閉じるといいます。量記号は Z を用います。単位は [Ω] です。

この式は、

　　L = C = 0　のとき　Z = R

　　R = C = 0　のとき　Z = ωL

　　R = L = 0　のとき　Z = \(\large{\frac{1}{ωC}}\)

になるので、抵抗のレジスタンス、コイルのリアクタンス、コンデンサーのリアクタンスは、インピーダンスの一種、という見方ができます。

最大値や実効値はベクトルの足し算

⑥式を Z を用いて表すと、

　　　　V₀ = ZI₀

となりますが、実効値というものが最大値を単純に \(\large{\frac{1}{\sqrt{2}\ }}\) 倍したものであることから、₀ を _e に入れ替えた式

　　　　V_e = ZI_e

も成り立っています。これらの式はオームの法則の式にそっくりです。しかし注意しなければならないことがあります。

上式に　Z = \(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\)　を入れ戻すと、

　　　　V_e = I_e\(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\)　　……⑦

　　　　　 = \(\sqrt{(RI_e)^{\small2}+(ωLI_e-\large{\frac{I_e}{ωC}})^{\small2}}\)

となりますが、コイルの V_Le = ωLI_e 、コンデンサーの V_Ce = \(\large{\frac{I_e}{ωC}}\) 、さらに V_Re = RI_e も合わせて代入すると、

　　　　V_e = \(\sqrt{{V_{\rm{Re}}}^{\small2}+(V_{\rm{Le}}-V_{\rm{Ce}})^{\small2}}\)

であり、この式は、実効値は単純に V_e = V_Re + V_Le + V_Ce と足し合わせてはいけないことを意味しています。

V_R 、V_L 、V_C には位相差があるので、最大値や実効値を求めるときは、単純な足し算ではなくベクトルの足し算をしなければなりません。瞬時値（瞬間値）を求めるときについては、各値に sin が含まれていて位相差が考慮されているので、上で計算したように単純に足し合わせることができます。

電力

RLC直列回路の消費電力 P を求めてみます。電力というものは電流と電圧を掛けたものですので、I = I₀sinωt と V = V₀sin(ωt + φ) ＊V = V₀sin(ωt + φ) という式は、
④式　V = I₀\(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\) sin(ωt + φ)　に、
⑥式　V₀ = I₀\(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\)　を代入したものです。
④式を簡略化して表したものです。
　 閉じるを掛け合わせますと、

　　　　P = I × V

　　　　　= I₀sinωt × V₀sin(ωt + φ)

　　　　　= I₀V₀sinωt⋅sin(ωt + φ)

三角関数の積和の公式　sinαsinβ = - \(\large{\frac{1}{2}}\)\(\bigl\{\)cos(α+β) - cos(α-β)\(\bigr\}\)　を適用しますと、

　　　　P = I₀V₀ × \(\Bigl[\) - \(\large{\frac{1}{2}}\)\(\bigl\{\)cos(ωt+ωt+φ) - cos(ωt-(ωt+φ))\(\bigr\}\Bigr]\)

　　　　　= I₀V₀ × \(\Bigl[\) - \(\large{\frac{1}{2}}\)\(\bigl\{\)cos(2ωt+φ) - cos(-φ)\(\bigr\}\Bigr]\)

　　　　　= I₀V₀ × \(\Bigl[\) - \(\large{\frac{1}{2}}\)\(\bigl\{\)cos(2ωt+φ) - cosφ\(\bigr\}\Bigr]\)

　　　　　= I₀V₀ × \(\Bigl[\) \(\large{\frac{1}{2}}\)\(\bigl\{\)cosφ - cos(2ωt+φ)\(\bigr\}\Bigr]\)

　　　　　= \(\large{\frac{1}{2}}\)I₀V₀\(\bigl\{\)cosφ - cos(2ωt+φ)\(\bigr\}\)

この式の第2項 cos(2ωt+φ) ＊ 『コイルを流れる交流』項『別解』の ＊ の中でも説明したことですが、
y = Asin(Bt + C) という式があるとき、

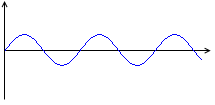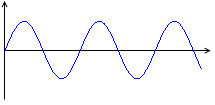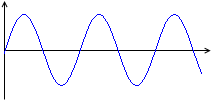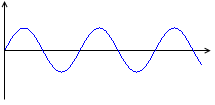　A は波の振幅（最大値）のことです。

　B は波の角速度（揺れの細かさ）のことです。

　C は基準位置からの位相（タイミング）のズレのことです。

A、B、Cがどのような値をとっても、この曲線は必ず 0（横軸）を中心にして振動しています。
y = Asin(Bt + C)×sint という形だったり、y = Asin(Bt + C) + D というような形であれば、0 を中心とした振動ではなくなります。
　 閉じる は 0 を中心にして振動しているので和をとる（時間平均をとる）と 0 ＊『コイルを流れる交流』項の『電力』の最後の＊の中の解説をお読みください。
　 閉じる。つまり平均の消費電力 P を式で表すと第1項だけが残り、

　　　　P = \(\large{\frac{1}{2}}\)I₀V₀\(\bigl\{\)cosφ\(\bigr\}\)

　　　　　 = \(\large{\frac{1}{2}}\)I₀V₀ cosφ

これを少し変形して、

　　　　P = \(\large{\frac{1}{\sqrt{2}\ }}\)⋅\(\large{\frac{1}{\sqrt{2}\ }}\) I₀V₀ cosφ

　　　　　= \(\large{\frac{1}{\sqrt{2}\ }}\) I₀ \(\large{\frac{1}{\sqrt{2}\ }}\) V₀ cosφ

実効値は最大値を単純に \(\large{\frac{1}{\sqrt{2}\ }}\) 倍したものであるので、I_e = \(\large{\frac{1}{\sqrt{2}\ }}\)I₀ 、V_e = \(\large{\frac{1}{\sqrt{2}\ }}\)V₀ を代入しますと、

　　　　P = I_eV_e cosφ

となります。

力率

上式左辺の cosφ という量は時間とともに変化するような量ではなく定数です。（ ωt という量は t が含まれていますので時間とともに変化する量です。）

④式で、

　　　　tanφ = \(\large{\frac{ωL-\large{\frac{1}{ωC}}}{R}}\)

と述べましたが、この φ を cos で表すと、

　cosφ = \(\large{\frac{RI_0}{V_0}}\)　　　　⑥式 V₀ = I₀\(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\) を代入して

　　　 = \(\large{\frac{RI_0}{I_0\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}}}\)

　　　 = \(\large{\frac{R}{\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}}}\)

となります。

cosx というものは最小値が -1 で、最大値が 1 ですが、上式の右辺は正ですので、0 ≦ cosφ ≦ 1 です。そしてよく見てみますと、

R = 0 のときは P = I_eV_e cosφ = 0 、つまり抵抗が 0 のとき（抵抗が無いとき）消費電力の和が 0 ということであり、このことは交流を流したコイルでは電力が消費されないことや、交流を流したコンデンサーでは電力が消費されないことを裏付けています。

この cosφ のことを力率といい（力率は高校物理の範囲外かも）、ωL = \(\large{\frac{1}{ωC}}\) のときに消費電力が P = I_eV_e cosφ = I_eV_e × 1 = I_eV_e となり、最も大きくなります。逆にいうと、最も電力の効率が良くなります。cosφ = 0.5 だったりすると電流なり電圧なりを倍にしないと目標の電力を得られなかったりします。

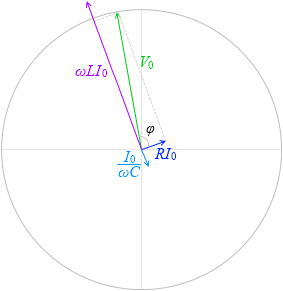R が 0 に近いときや、ωL と \(\large{\frac{1}{ωC}}\) の差が大きいときというのは φ が \(\large{\frac{π}{2}}\) か - \(\large{\frac{π}{2}}\) に近くなります。力率が悪い場合です。

R が大きいときや、ωL と \(\large{\frac{1}{ωC}}\) の差が小さいときというのは φ が 0 に近くなります。力率が良い場合です。

（『共振周波数』もご参照ください。）

接続の順序を入れ替えても

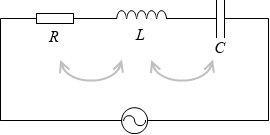RLC直列回路において接続する順序を入れ替えたりしても、

インピーダンスの式、

　　Z = \(\sqrt{R^{\small2}+(ωL-\large{\frac{1}{ωC}})^{\small2}}\)

に変化はありません。

ωL と \(\large{\frac{1}{ωC}}\) の順序が入れ替わるようなことはありません。\(\large{\frac{1}{ωC}}\) の前に - の符号が付くのは元をたどると位相差を起因としています。接続の順序ではありません。