万有引力による位置エネルギー
万有引力は保存力なので位置エネルギーがある
万有引力は保存力ですので、重力や弾性力のように、位置エネルギーがあるとみなせます。
保存力というのは重力や弾性力のように、物体の移動経路によらず仕事が一定になるような力です。他方の非保存力というのは摩擦力や空気抵抗のように物体の移動経路によって仕事の大きさが変わってしまうような力です。
保存力が発揮されている空間においては、位置だけで決まるエネルギーがあるとみなせます。
重力、弾性力の位置エネルギーのおさらい
重力による位置エネルギーは、mgh です。質量 m の物体が高さ h の位置に置いてあるだけで mgh という量の位置エネルギーを持ちます。
弾性力による位置エネルギーは、\(\large{\frac{1}{2}}\)kx2 です。ばね定数 k のばねを x だけ伸ばした先に取り付けた物体はそこにあるだけで \(\large{\frac{1}{2}}\)kx2 という量の位置エネルギーを持ちます。
これらの位置エネルギーの量というのは、基準の位置から物体を動かしたときの仕事の量のことでした。仕事の大きさは、力を受けながら移動した距離で決まります。
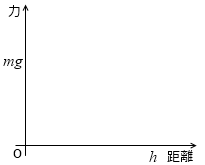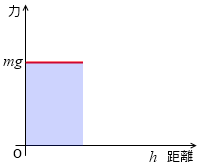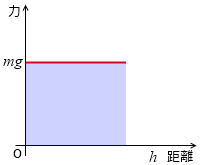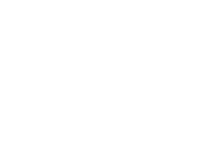 重力による位置エネルギーの大きさは、mg という力を受けながら距離 h だけ移動したときの仕事の大きさです。左図の青色部分の面積のことです。
重力による位置エネルギーの大きさは、mg という力を受けながら距離 h だけ移動したときの仕事の大きさです。左図の青色部分の面積のことです。
mg を h で積分したものがそれであり、値は mgh です。
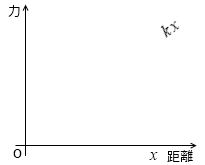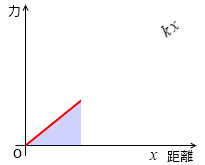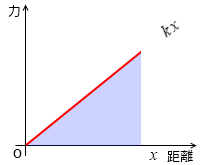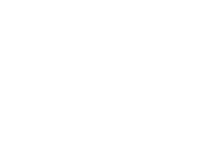 弾性力による位置エネルギーの大きさは、kx という力を受けながら距離 x だけ移動したときの仕事の大きさです。左図の青色部分の面積のことです。
弾性力による位置エネルギーの大きさは、kx という力を受けながら距離 x だけ移動したときの仕事の大きさです。左図の青色部分の面積のことです。
kx を x で積分したものがそれであり、値は \(\large{\frac{1}{2}}\)kx2 です。
万有引力の位置エネルギーを定義したいけれど
万有引力の大きさは F = G\(\large{\frac{Mm}{r^2}}\) です。(物体Aの質量を M 、物体Bの質量を m 、物体Aの中心から物体Bの中心までの距離を r 、万有引力定数を G とします。位置を示す変数は r だけです。今は M と m は定数とみなします。)
上にならって考えますと、万有引力による位置エネルギーというのは G\(\large{\frac{Mm}{r^2}}\) を r で積分したものといえます。
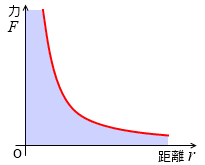 F = G\(\large{\frac{Mm}{r^2}}\) のグラフを描いてみますと左図のようになります。
F = G\(\large{\frac{Mm}{r^2}}\) のグラフを描いてみますと左図のようになります。
この曲線と r軸で挟まれた部分が積分した値であり、位置エネルギーです。
しかし、r = 0 付近における F の値が無限大になってしまっています。
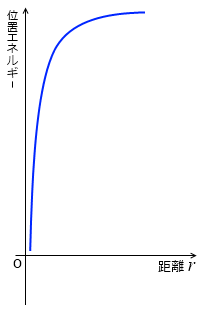 積分して無理やり位置エネルギーを求めてグラフにすると左図のようになります。
積分して無理やり位置エネルギーを求めてグラフにすると左図のようになります。
なんかやな感じです。もうちょっとなんとかしたいです。
基準位置を工夫する
位置エネルギーというものは主に、2つの地点における位置エネルギーの「差」が問題になるので、基準位置はどこでもいいのです。
基準として妥当なところはどこでしょうか。
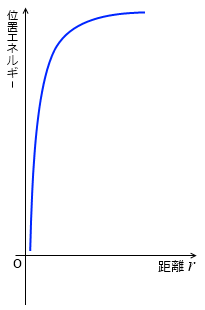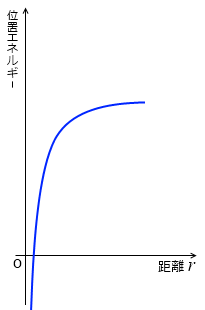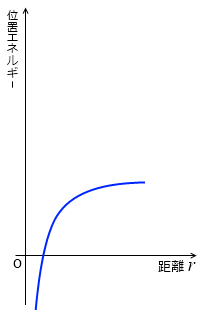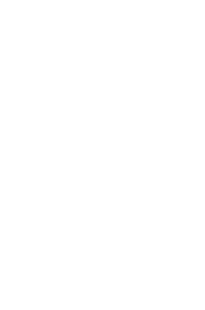 それは「距離が無限遠」のところです。r = ∞ のとき位置エネルギーを 0 、と定めるといい感じになります。
それは「距離が無限遠」のところです。r = ∞ のとき位置エネルギーを 0 、と定めるといい感じになります。
どういうことか、以下説明します。
積分
ここで積分についておおざっぱに説明します。詳しいことは数学の教科書を見てください。
3 や 4 や 9 や 15 などの定数を x で微分すると 0 です。
x を x で微分すると 1 です。
x2 を x で微分すると 2x です。
x3 を x で微分すると 3x2 です。
x4 を x で微分すると 4x3 です。
x-1 を x で微分すると - x -2 です。*x-1 というのは \(\large{\frac{1}{x}}\) のことで、x -2 というのは \(\large{\frac{1}{x^2}}\) のことです。
閉じる
積分は微分の逆です。
0 を x で積分すると 3 や 4 や 9 や 15 などになります。 3 や 4 や 9 や 15 などをまとめて C とおきます。
1 を x で積分すると x + C です。*1 というのは 1+0 であるので、それを積分すると x+3 になったり、x+4 になったりします。
閉じる
x を x で積分すると \(\large{\frac{1}{2}}\)x2 + C です。*x2 の微分が 2x であるので、これはつまり、\(\large{\frac{1}{2}}\)x2 の微分が x です。
閉じる
x2 を x で積分すると \(\large{\frac{1}{3}}\)x3 + C です。*x3 の微分が 3x2 であるので、これはつまり、\(\large{\frac{1}{3}}\)x3 の微分が x2 です。
閉じる
x -2 を x で積分すると - x-1 + C です。*x-1 の微分が - x -2 であるので、これはつまり、- x -1 の微分が x -2 です。
閉じる
こういうわけで、mg を h で積分したものが mgh であり、kx を x で積分したものが \(\large{\frac{1}{2}}\)kx2 であったわけです。そしてこれらのときは C を 0 とおいていたわけです。
万有引力のときも C=0 とおく
x -2 を x で積分すると - x-1 + C ですので、
万有引力 F = G\(\large{\frac{Mm}{r^2}}\) を r で積分しますと - G\(\large{\frac{Mm}{r}}\) + C となります。
このとき C を 0 としたものを万有引力による位置エネルギー U と定めてみます。つまり、
U = - G\(\large{\frac{Mm}{r}}\)
となりますが、位置エネルギーの基準、つまり位置エネルギー U が 0 となるとき、r はどのような値をとるでしょうか。
0 = - G\(\large{\frac{Mm}{r}}\)
∴ r = ∞
です。距離が無限遠のときに位置エネルギーが 0 となります。
あるいは、r が無限遠のときを基準とするのではなく、地球の半径の位置、つまり地表の位置を位置エネルギーの基準とする考え方もあるかもしれません。
そのときの C はどのように定めたらよいでしょうか。
地球の半径を R とします。r = R のとき位置エネルギー U が 0 になるということだから、
U = 0 = - G\(\large{\frac{Mm}{R}}\) + C
∴ C = G\(\large{\frac{Mm}{R}}\)
つまり位置エネルギーを U = - G\(\large{\frac{Mm}{r}}\) + G\(\large{\frac{Mm}{R}}\) と定めることになります。しかしこれですと、地表付近の物体の位置エネルギーを考えるときにはいいかもしれませんが、他の一般の物体について考えるときは不合理です。R より近い距離では位置エネルギーが負になり、R より遠い距離では位置エネルギーが正になるなんて面倒です。
やはり、無限遠のときの位置エネルギーを 0 とおき、位置エネルギーは常に負であるけれども、距離が近いときほど位置エネルギーは小さく、距離が遠いほど位置エネルギーは大きくなる、というのが妥当です。つまり C = 0 とするのが合理的です。
万有引力による位置エネルギー
U = - G\(\large{\frac{Mm}{r}}\)
エネルギーですので単位は [J] ジュール です。
あらためてグラフを描いてみます。
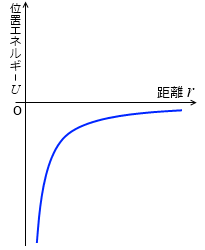 2物体の距離 r が近いときは位置エネルギー U がとてつもなく小さく、距離が遠いほど位置エネルギーは大きくなっていき、その最大値は 0 です。
2物体の距離 r が近いときは位置エネルギー U がとてつもなく小さく、距離が遠いほど位置エネルギーは大きくなっていき、その最大値は 0 です。
くれぐれも、
r は地表からの高さではなく2物体の中心と中心との距離であること、
距離が遠いほど位置エネルギーは大きくなる、0 に近づくからといって小さくなるのではなく大きくなる、
ということを忘れないでください。
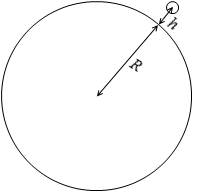 地球を物体A、地表付近の物体を物体Bとし、物体Aの質量を M 、物体Bの質量を m 、物体Aの半径を R 、地表面から物体Bの距離を h 、万有引力定数を G 、重力加速度を g とします。
地球を物体A、地表付近の物体を物体Bとし、物体Aの質量を M 、物体Bの質量を m 、物体Aの半径を R 、地表面から物体Bの距離を h 、万有引力定数を G 、重力加速度を g とします。