qI782

図2のように、抵抗の無視できる断面積 S の N 回巻きコイルを、ダイオード、抵抗器およびスイッチからなる回路につなぎ、時間 t とともに変化する一様な磁束密度 B の磁場（磁界）の中に置いた。コイルの中心軸は磁場の方向に平行であり、B は図の矢印の向きを正とする。ただし、コイルの自己誘導の影響はないものとする。図中のダイオードは、左から右にのみ電流を流す。

図 2

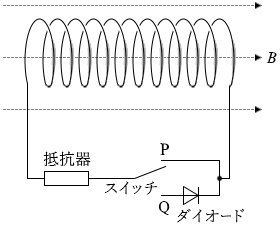
（問3）スイッチをP側に入れて、磁束密度 B を図3のように変化させた。三つの時間範囲（ 0 < t < T 、T < t < 2T 、2T < t < 3T ）における、抵抗器を流れる電流に関する記述の組合せとして最も適当なものを、下の①～⑧のうちから一つ選べ。

図 3
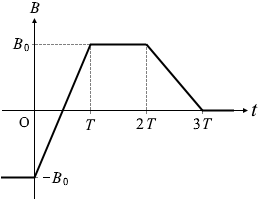
0 < t < T T < t < 2T 2T < t < 3T
① 流れる 流れる 流れる
② 流れる 流れる 流れない
③ 流れる 流れない 流れる
④ 流れる 流れない 流れない
⑤ 流れない 流れる 流れる
⑥ 流れない 流れる 流れない
⑦ 流れない 流れない 流れる
⑧ 流れない 流れない 流れない

　

（問4）次に、スイッチをQ側に入れて、磁束密度 B を図3のように変化させた。抵抗器に電流が流れるとき、コイル両端の電圧の大きさを式で表わせ。

#センター17本試物理

（問3）
この回路には電源がありません。電流が流れるとしたらそれは電磁誘導が起こるからです。電磁誘導は磁束（磁束密度）が変化することで起こります。

　0 < t < T …… 磁束密度が急激に増えている。電流が流れる。

　T < t < 2T …… 磁束密度は変化してない。電流は流れない。

　2T < t < 3T …… 磁束密度が減っている。電流が流れる。

答えは ③ です。

　

　

（問4）
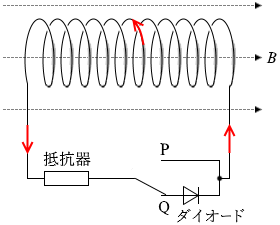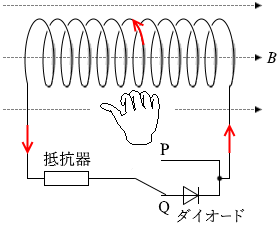ダイオードは三角形の尖った方の向きにしか電流を流しませんから、回路に電流が流れるときのその向きは左図のような向きです。

このような向きに電流が発生するのは、レンツの法則により、右向きの磁束が”増える”ときです。

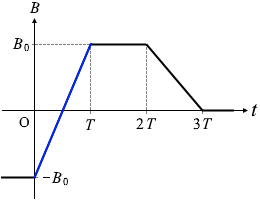右向きの磁束（磁束密度）が増えるのは 0 < t < T の間であり、2B0 だけ増えています。

コイル両端に電圧（誘導起電力）が発生するのは電磁誘導が起こるからであり、その誘導起電力（V とする。磁束を Φ とする）は

　　　　V = - N\(\large{\frac{ΔΦ}{Δt}}\)

であり、その大きさは

　　　　V = N\(\large{\frac{ΔΦ}{Δt}}\)　　（磁束Φ = 磁束密度B × 断面積S だから）

　　　　　 = N\(\large{\frac{Δ(BS)}{Δt}}\)　　（いま、S は一定だから）

　　　　　 = NS\(\large{\frac{ΔB}{Δt}}\)　　（T の間に 2B0 だけ変化するから）

　　　　　 = NS\(\large{\frac{2B_0}{T}}\)

　　　　　 = \(\large{\frac{2B_0SN}{T}}\)

　

　

（余談）
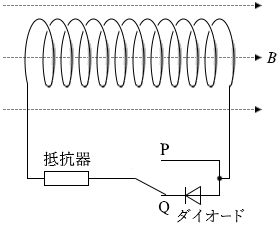もしダイオードの向きが逆だった場合は

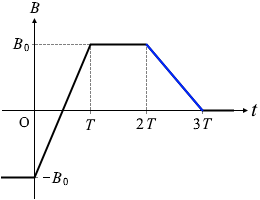電流の向きも逆になり、その向きに電流が発生するのは右向きの磁束が”減る”ときであり、

それは 2T < t < 3T の間であり、その間、B0 だけ減っているので、

発生する電圧（誘導起電力）の大きさは

　　　　V = N\(\large{\frac{ΔΦ}{Δt}}\)

　　　　　 = N\(\large{\frac{Δ(BS)}{Δt}}\)

　　　　　 = NS\(\large{\frac{ΔB}{Δt}}\)

　　　　　 = NS\(\large{\frac{B_0}{T}}\)

　　　　　 = \(\large{\frac{B_0SN}{T}}\)

です。問4の半分です。

↑ ↓