三つの抵抗器A、B、Cがある。Aの抵抗値は R1 で、BとCの抵抗値はともに R2 である。これらの抵抗値を、起電力が E で内部抵抗が無視できる電池と二つのスイッチS1、S2に図1のように接続した。
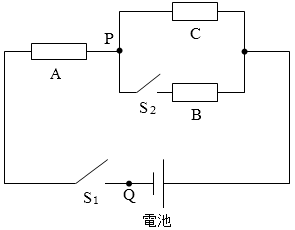
(問1)次の文章中の空欄1⋅2に入れる式として正しいものを、下の①~⑧のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
まず、S1とS2をともに開いた状態で、点Pと点Qの間の電位差(電圧)を測定したところ1であった。次に、S1とS2をともに閉じたら、点Pと点Qの間の電位差は2となった。
① 0 ② E ③ \(\large{\frac{R_1E}{R_2}}\) ④ \(\large{\frac{R_1E}{2R_2}}\) ⑤ \(\large{\frac{R_2E}{R_1}}\) ⑥ \(\large{\frac{R_2E}{2R_1}}\) ⑦ \(\large{\frac{2R_1E}{2R_1+R_2}}\) ⑧ \(\large{\frac{R_2E}{2R_1+R_2}}\)
(問2)S1とS2をともに閉じたときに電池が供給する電力(仕事率)を W1 とし、S1を閉じS2を開いたときに電池が供給する電力を W2 とする。\(\large{\frac{W_1}{W_2}}\) を表す式として正しいものを、次の①~⑥のうちから一つ選べ。
① \(\large{\frac{R_1+R_2}{2R_1+R_2}}\) ② \(\large{\frac{R_1+R_2}{R_1+2R_2}}\) ③ \(\large{\frac{2R_1+2R_2}{2R_1+R_2}}\) ④ \(\large{\frac{2R_1+R_2}{2R_1+R_2}}\) ⑤ \(\large{\frac{R_1}{2R_2}}\) ⑥ \(\large{\frac{R_2}{2R_1}}\)
#センター09追試
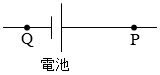 回路はこのようなものと同等であり、
回路はこのようなものと同等であり、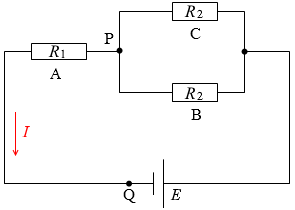 まず、BとCを合わせた抵抗(RBCと置く)は、
まず、BとCを合わせた抵抗(RBCと置く)は、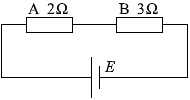
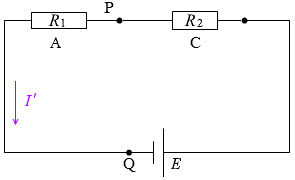 S1を閉じS2を開いたときは、
S1を閉じS2を開いたときは、