図1に示すように、極板の面積がすべて等しい平行板コンデンサー C1、C2、C3がある。極板間の距離はC1、C2では d で、C3では \(\large{\frac{d}{2}}\) である。また、コンデンサーC1、C3は空気で、C2は比誘電率 3.0 の誘電体でそれぞれ満たされている。
（問1）電気容量の大きいものから順に並べよ。
（問2）図1のコンデンサーC1 、C2、C3を用いて図2のような回路を組んだ。 すべてのコンデンサーに電荷がない状態から、スイッチSをa側にたおしてコンデンサーC1を起電力 9.0V の電池で充電した。次にスイッチSをb側に切り替えた。図2の端子1、2の間の電位差はいくらになるか。
#センター01本試
（問1）
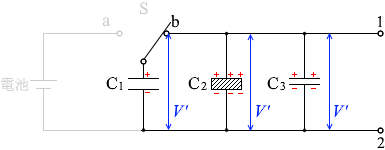
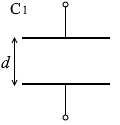
コンデンサーC1の電気容量を C1 としますと、
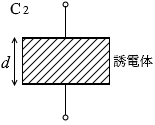
コンデンサーC2の電気容量は 3.0C1 です。比誘電率 εr の誘電体で満たすと電気容量は εr倍 になります。
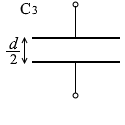
コンデンサーC3の電気容量は 2.0C1 です。C = \(\large{\frac{1}{4\pi k}\frac{S}{d}}\) です。極板の面積に比例し、極板間に反比例します。
答え： C2 、C3、C1
（問2）
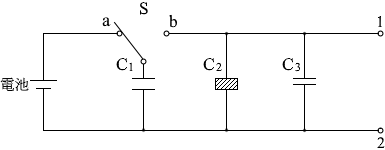
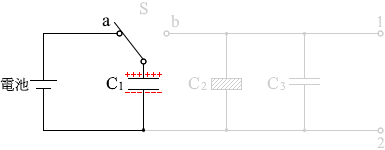スイッチSをa側にたおしたときの、コンデンサーC1に蓄えられた電気量を Q1 としますと、Q = CV の関係より、
Q1 = C1 × 9.0 = 9.0C1
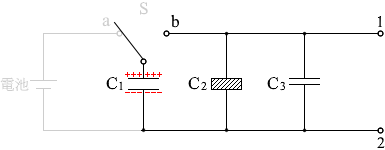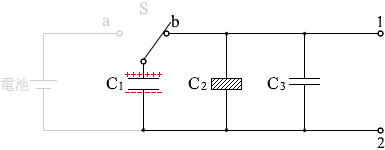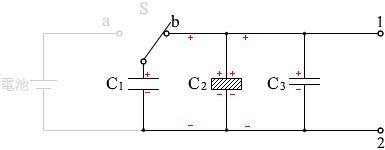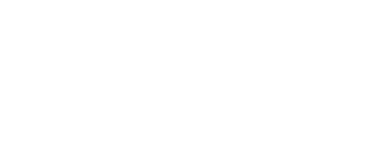スイッチSをb側に切り替えますと、電荷はC2 、C3へ移動していきます。
各電圧が等しくなるまで移動します。
この電圧を V' と置きますと、
Q = CV の関係より、
C1 の電気量： C1 × V'
C2 の電気量： 3.0C1 × V'
C3 の電気量： 2.0C1 × V'
そして、電気量保存の法則より、これらの総計は元々の電気量 Q1 に等しいから、
C1V' + 3.0C1V' + 2.0C1V' = 9.0C1
∴ V' + 3.0V' + 2.0V' = 9.0
∴ 6.0V' = 9.0
∴ V' = 1.5 [V]
と求まります。
（別解）
慣れれば暗算で解くこともできます。
3つのコンデンサーの合成容量は
C1 + 3.0C1 + 2.0C1 = 6.0C1
であり、電気量保存の法則と Q = CV の関係より、電気容量が6倍になれば電圧は\(\large{\frac{1}{6}}\)倍になり、
\(\large{\frac{1}{6}}\)×9.0 = 1.5 [V]
と導き出せます。