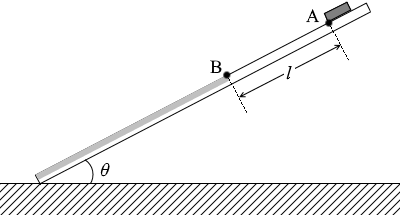
図1のように、板を用いて水平な床の上に傾きの角 θ の斜面をつくる。板の表面は、物体の底面との間の摩擦係数が点Bより上の部分と下の部分で異なるように加工されている。この斜面上の点Aに置かれた質量 m の小さな物体の運動を考えよう。
(問1)斜面の傾きをゆっくりと大きくしていくと、点Aに静止していた物体が角度 θ = θ0 のとき滑り出した。θ0 が満たす式として正しいものを、次の①~⑥のうちから一つ選べ。ただし、点Aでの静止摩擦係数を μ とする。
① sinθ0 = μ ② cosθ0 = μ ③ tanθ0 = μ
④ sinθ0 = \(\large{\frac{1}{μ}}\) ⑤ cosθ0 = \(\large{\frac{1}{μ}}\) ⑥ tanθ0 = \(\large{\frac{1}{μ}}\)
(問2)次に、角度 θ を θ0 より大きな値に固定して点Aに物体を置いたところ、初速度 0 で滑りはじめた。点Bより上の部分での動摩擦係数が μ' であるとき、点Bでの物体の速さ v はいくらか。ただし、点Aと点Bの間の距離を l とし、重力加速度の大きさを g とする。
(問3)問2において、点Bを通過したあと、物体は斜面上のある点で静止した。点Bを通過する時刻を t0 とするるとき、速さ v の時間変化を表すグラフとして最も適当なものを、次の①~⑥のうちから一つ選べ。
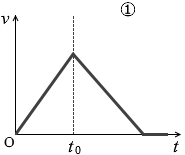
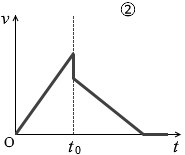
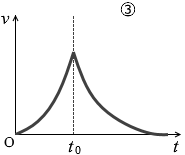
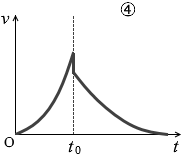
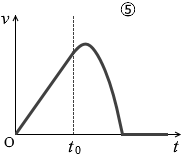
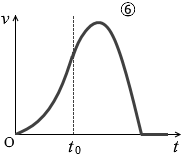
#センター07本試
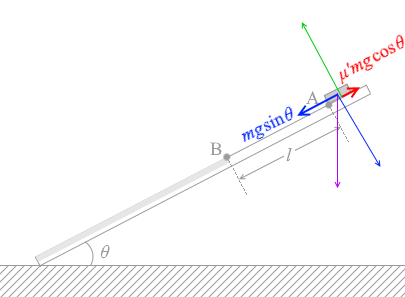 物体に掛かる重力は
物体に掛かる重力は 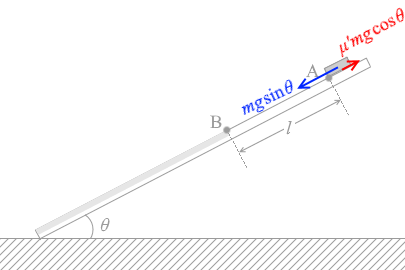 点B以前は、上で示した運動方程式
点B以前は、上で示した運動方程式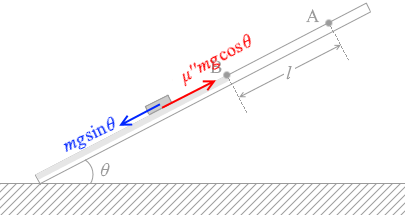 点B以降は動摩擦係数が大きくて(μ'' と置きます)
点B以降は動摩擦係数が大きくて(μ'' と置きます)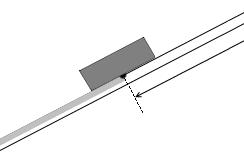 点Bをまたぐ瞬間というのは、摩擦係数が μ' の場所と μ'' の場所が混ざっているわけですから、徐々に速度が変化するということになります。
点Bをまたぐ瞬間というのは、摩擦係数が μ' の場所と μ'' の場所が混ざっているわけですから、徐々に速度が変化するということになります。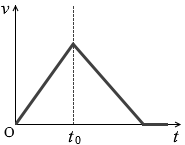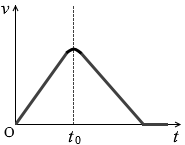 v-tグラフの曲線の頂上は少し角が取れるはずです。
v-tグラフの曲線の頂上は少し角が取れるはずです。