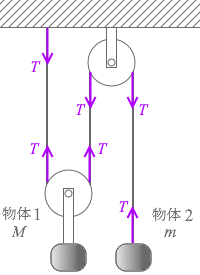
図1のように、二つの滑車と伸び縮みしないひもを使い、質量 M の物体1と質量 m の物体2をつりさげた。はじめ、物体1、2は動かないように手で支えられている。静かに手を離したところ、物体1、2が運動し始めた。このときの物体1の加速度を α 、物体2の加速度を β とする。ただし、加速度は鉛直下向きを正とする。また、滑車とひもの質量は無視でき、滑車はなめらかに回転するものとする。
(問1)加速度 α と β の間に成り立つ関係として正しいものを、次の①~⑥のうちから一つ選べ。
① β = 2α ② β = α ③ 2β = α
④ β = - 2α ⑤ β = - α ⑥ 2β = - α
(問2)物体1、2の運動方程式の組み合わせとして正しいものを、次の①~④のうちから一つ選べ。ただし、ひもの張力を T とし、重力加速度の大きさを g とする。
① \(\begin{cases} Mα = Mg-2T \\ mβ = mg-T \end{cases}\) ② \(\begin{cases} Mα = mg-2T \\ mβ = Mg-T \end{cases}\)
③ \(\begin{cases} Mα = (M+m)g-T \\ mβ = (M+m)g-2T \end{cases}\) ④ \(\begin{cases} Mα = (M+m)g-2T \\ mβ = (M+m)g-T \end{cases}\)
(問3)次の文中の空欄3に入れる式として正しいものを、下の①~⑤のうちから一つ選べ。
物体1は、M > 3 のとき降下するが、M < 3 のときには上昇する。
① \(\large{\frac{m}{3}}\) ② \(\large{\frac{m}{2}}\) ③ m
④ 2m ⑤ 3m
#センター06追試
 まず、
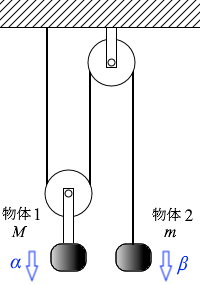
まず、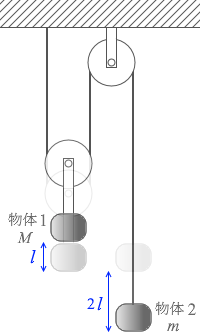 次に、
次に、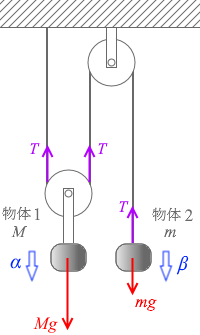 各物体にはたらく力を描くと左図のようになります。
各物体にはたらく力を描くと左図のようになります。