（問1）
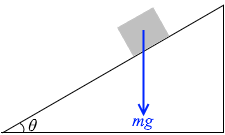物体には重力mg が掛かり、
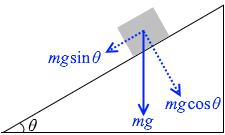それを【斜面方向】と【斜面に垂直な方向】に分解しますと、mgsinθ と mgcosθ となり、
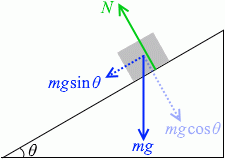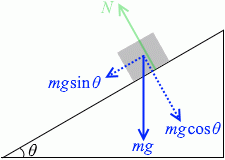物体は【斜面に垂直な方向】には動かないから、これは【斜面に垂直な方向】にはたらく力がつり合っているということであり、
N = mgcosθ
です。
（問2）
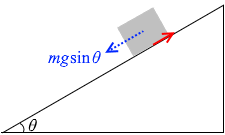物体が動く方向は斜面方向であり、その方向の力は mgsinθ と摩擦力（動摩擦力）の2つです。
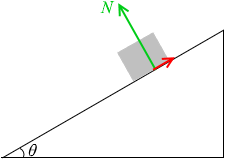摩擦力（動摩擦力）というのは垂直抗力に摩擦係数（動摩擦係数）を掛けたものだから、
N × μ'
です。
（正負に気をつけて）2つの力を合わせますと、
mgsinθ - μ'N
であり、求める加速度を a と置いて斜面方向の運動方程式（ma = F）を立てますと、
ma = mgsinθ - μ'N
∴ a = gsinθ - \(\large{\frac{μ'N}{m}}\)
答えは ③ です。
（別表現）
N を用いないで表現しますと（上式に N = mgcosθ を代入して）、
a = gsinθ - μ'gcosθ = g(sinθ - μ'cosθ)
となります。
（頻出）
この問題は頻出です。高校の定期テストでも大学入試でもよく出題されます。しっかり覚えましょう。