(問3)
衝突前の力学的エネルギーは
(運動エネルギー)+(弾性エネルギー)= \(\large{\frac{1}{2}}\)(M + m)v2 + 0
d1 だけ縮んだときの力学的エネルギーは
(運動エネルギー)+(弾性エネルギー)= 0 + \(\large{\frac{1}{2}}\)kd12
力学的エネルギー保存の法則より、
\(\large{\frac{1}{2}}\)(M + m)v2 + 0 = 0 + \(\large{\frac{1}{2}}\)kd12
∴ (M + m)v2 = kd12
∴ d12 = \(\large{\frac{M+m}{k}}\)v2
∴ d1 = \(\sqrt{\frac{M+m}{k}}\)v
(問4)
ア
d < d2 のときは台と小物体は一体であると考えることができ、質量 (M + m) の物体が弾性力 kd を受けて減速する運動であるとみなすことができるので、その加速度の大きさを a と置くと、
(M + m)a = kd
という運動方程式が立てられます。つまり、加速度の大きさは
a = \(\large{\frac{kd}{M+m}}\)
イ
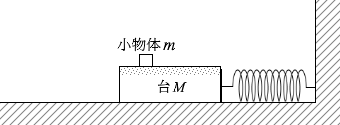 台がばねに衝突すると弾性力を受けて減速するわけですが、
台がばねに衝突すると弾性力を受けて減速するわけですが、
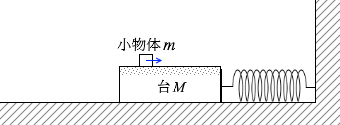 上に載っている小物体は慣性で右へ進もうとします。つまり慣性力を受けるわけです。
上に載っている小物体は慣性で右へ進もうとします。つまり慣性力を受けるわけです。
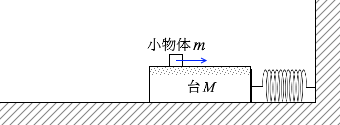 ばねの弾性力というのは縮めば縮むほど大きくなるものです。つまり、アで導き出した加速度 a = \(\large{\frac{kd}{M+m}}\) というのは縮めば縮むほど大きくなります。(縮めば縮むほど急激に減速するということです。これが摩擦力による減速との大きな違いです。摩擦力による減速では加速度は一定です。)
ばねの弾性力というのは縮めば縮むほど大きくなるものです。つまり、アで導き出した加速度 a = \(\large{\frac{kd}{M+m}}\) というのは縮めば縮むほど大きくなります。(縮めば縮むほど急激に減速するということです。これが摩擦力による減速との大きな違いです。摩擦力による減速では加速度は一定です。)
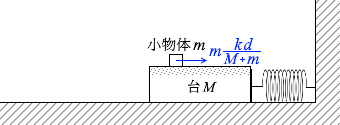 台が \(\large{\frac{kd}{M+m}}\) の加速度で減速するとき、小物体の受ける慣性力は m\(\large{\frac{kd}{M+m}}\) です。
台が \(\large{\frac{kd}{M+m}}\) の加速度で減速するとき、小物体の受ける慣性力は m\(\large{\frac{kd}{M+m}}\) です。
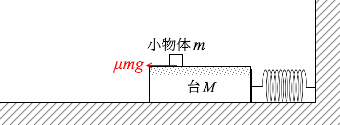 一方、台と小物体との間の静止摩擦係数が μ であるので、台と小物体との間の最大静止摩擦力は μmg で、
一方、台と小物体との間の静止摩擦係数が μ であるので、台と小物体との間の最大静止摩擦力は μmg で、
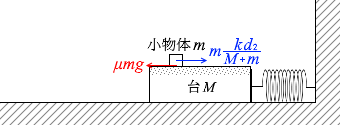 ばねが d2 だけ縮んだ瞬間というのは、慣性力が m\(\large{\frac{kd_2}{M+m}}\) で、これが最大静止摩擦力と同じ大きさになっているという状態です。(これ以上縮むと慣性力の方が大きくなり小物体は滑り始めます。)
ばねが d2 だけ縮んだ瞬間というのは、慣性力が m\(\large{\frac{kd_2}{M+m}}\) で、これが最大静止摩擦力と同じ大きさになっているという状態です。(これ以上縮むと慣性力の方が大きくなり小物体は滑り始めます。)
つまり、
m\(\large{\frac{kd_2}{M+m}}\) = μmg
∴ \(\large{\frac{kd_2}{M+m}}\) = μg
∴ d2 = \(\large{\frac{M+m}{k}}\)μg
(慣性力を感じるのは台と一緒に動いている観測者です。m\(\large{\frac{kd_2}{M+m}}\) = μmg という式は小物体が静止していることを表すつり合いの式ですが、小物体が静止しているように感じるのは台と一緒に動いている観測者です。台と一緒に動いている観測者から見た世界を非慣性系といいます。)
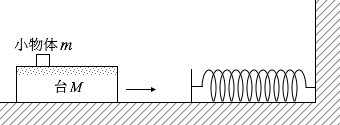
 台がばねに衝突すると弾性力を受けて減速するわけですが、
台がばねに衝突すると弾性力を受けて減速するわけですが、 上に載っている小物体は慣性で右へ進もうとします。つまり
上に載っている小物体は慣性で右へ進もうとします。つまり ばねの弾性力というのは縮めば縮むほど大きくなるものです。つまり、
ばねの弾性力というのは縮めば縮むほど大きくなるものです。つまり、 台が \(\large{\frac{kd}{M+m}}\) の加速度で減速するとき、小物体の受ける
台が \(\large{\frac{kd}{M+m}}\) の加速度で減速するとき、小物体の受ける 一方、台と小物体との間の静止摩擦係数が μ であるので、台と小物体との間の
一方、台と小物体との間の静止摩擦係数が μ であるので、台と小物体との間の ばねが d2 だけ縮んだ瞬間というのは、慣性力が m\(\large{\frac{kd_2}{M+m}}\) で、これが最大静止摩擦力と同じ大きさになっているという状態です。(これ以上縮むと慣性力の方が大きくなり小物体は滑り始めます。)
ばねが d2 だけ縮んだ瞬間というのは、慣性力が m\(\large{\frac{kd_2}{M+m}}\) で、これが最大静止摩擦力と同じ大きさになっているという状態です。(これ以上縮むと慣性力の方が大きくなり小物体は滑り始めます。)