図5のように、エレベーターの天井に固定された、なめらかに回る軽い滑車に軽い糸をかけ、糸の両端に質量 M と質量 m（M > m）の物体を取り付けた。重力加速度の大きさを g とする。
（問4）エレベーターが静止しているとき、糸がたるまないように二つの物体を支えた状態から静かに放すと、物体は鉛直方向に動き始めた。このとき、糸の張力の大きさ T を式で表わせ。
（問5）図6のように、質量 m の物体の代わりに床に固定したばね定数 k の軽いばねを取り付けた。鉛直上向きに大きさ a の加速度で等加速度運動しているエレベーターの中で、質量 M の物体がエレベーターに対して静止していた。このとき、ばねの自然の長さからの伸び x を式で表わせ。
#センター17本試物理
（問4）
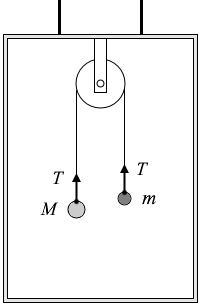
『滑車につるされた2物体』で説明したように運動方程式を立てますと、（加速度を α とします）
全体 ： (M + m)α = Mg - mg
重い方 ： Mα = Mg - T
軽い方 ： mα = T - mg
2番目の式を変形して、
α = \(\large{\frac{Mg-T}{M}}\)
3番目の式に代入して、
m\(\large{\frac{Mg-T}{M}}\) = T - mg
∴ Mmg - mT = MT - Mmg
∴ Mmg + Mmg = MT + mT
∴ 2Mmg = (M + m)T
∴ T = \(\large{\frac{2Mm}{M+m}}\)g
（問5）
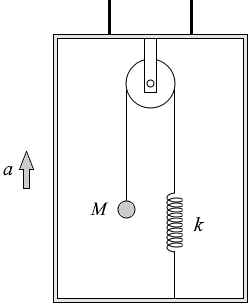
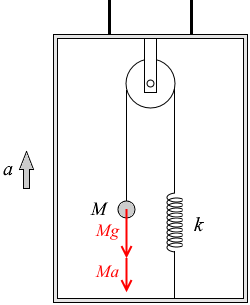エレベーターは鉛直上向きに加速度 a で加速しているので、質量 M の物体に掛かる慣性力は下向きに Ma で、重力と合わせて Mg + Ma の力が質量 M の物体に掛かっています。
そして張力はどこもかしこも同じ大きさなので、ばねにも Mg + Ma の力が掛かっています。
フックの法則の式を立てますと、
Mg + Ma = kx
∴ M(g + a) = kx
∴ x = \(\large{\frac{M(g+a)}{k}}\)
（余談）
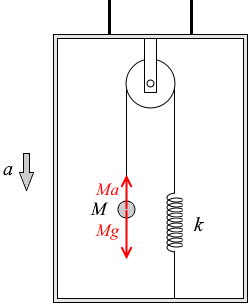エレベーターが鉛直下向きに加速度 a で加速していれば、質量 M の物体に掛かる慣性力は上向きに Ma で、重力と合わせて Mg - Ma の力が質量 M の物体に掛かることになります。
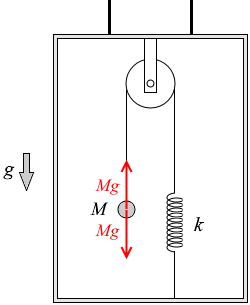このとき a = g であれば、質量 M の物体に掛かる力は 0 となり、ばねに掛かる力も 0 となります。
これはエレベーターのロープが切れた状態です。フリーフォールの状態です。