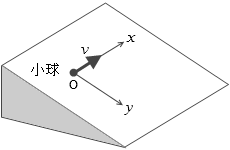
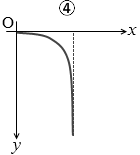
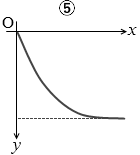
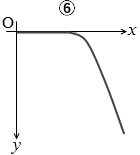
図2のように、一定の傾きをもったなめらかな斜面上の点Oに小球を置き、斜面に沿って水平方向の初速度 v を与えた。図のように点Oを原点として斜面上で水平方向に x軸を、それと直交して斜面を下降する方向に y軸をとったとき、斜面を滑り落ちる物体の軌跡として最も適当なものを、下の①~⑥のうちから一つ選べ。
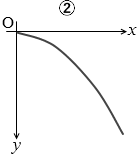
#センター08追試
図2のように、一定の傾きをもったなめらかな斜面上の点Oに小球を置き、斜面に沿って水平方向の初速度 v を与えた。図のように点Oを原点として斜面上で水平方向に x軸を、それと直交して斜面を下降する方向に y軸をとったとき、斜面を滑り落ちる物体の軌跡として最も適当なものを、下の①~⑥のうちから一つ選べ。


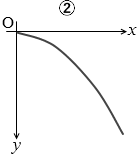




#センター08追試
初速度を与えたこと以外に小球に影響を与えるものは重力だけです。
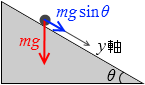 そして、小球が運動可能な方向の重力の成分は mgsinθ です(斜面の傾きの仰角を θ とします)。
そして、小球が運動可能な方向の重力の成分は mgsinθ です(斜面の傾きの仰角を θ とします)。
つまり、小球は x軸方向には等速直線運動をし、y軸方向には等加速度運動をします。加速度が gsinθ の等加速度運動です
y軸方向の運動方程式を立てると
may = mgsinθ
∴ ay = gsinθ
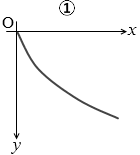
。この運動の軌跡は水平投射と同じように放物線となります。
答えは ② です。
(一応軌跡を表す式を求めてみます)
x軸方向の t秒後の位置は
x = vt
y軸方向の t秒後の位置は、等加速度直線運動の3式のうちの二番目の式より、
y = \(\large{\frac{1}{2}}\)gsinθt2
上の2式から t を消去しますと、
y = \(\large{\frac{1}{2}}\)gsinθ(\(\large{\frac{x}{v}}\))2
∴ y = \(\large{\frac{g\sinθ}{2v^2}}\)x2
\(\large{\frac{g\sinθ}{2v^2}}\) は定数ですから、この式は2次関数の式であり、その曲線は放物線を描きます。
(④?)
選択肢のうち④も正解かどうか迷いますが、カーブが若干直角に近いので放物線とはいえません。
(余談)
斜面における自由落下運動や水平投射は、重力の小さいどこかの惑星での運動と同じになるといえます。重力が g ではなく、もっと小さくなって gsinθ になったとみなすことができます。