CD
= - (U D - U C )
= - \(\large{\frac{3}{2}}\)RT D + 3RT B ……❸
(D→A:定積変化)定積変化 (W = 0)では、
W DA = 0 ……❹
➊、➋、❸、❹より、
W = W AB + W BC + W CD + W DA
= - \(\large{\frac{3}{2}}\)RT B + \(\large{\frac{3}{2}}\)RT A + Q 1 - 3RT B + \(\large{\frac{3}{2}}\)RT B - \(\large{\frac{3}{2}}\)RT D + 3RT B + 0
= \(\large{\frac{3}{2}}\)RT A + Q 1 - \(\large{\frac{3}{2}}\)RT D 問2の結果を代入して
= \(\large{\frac{3}{2}}\)RT A + \(\large{\frac{5}{2}}\)RT B - \(\large{\frac{3}{2}}\)RT D
= \(\large{\frac{R}{2}}\)(3T A + 5T B - 3T D )
と、同じ結果が得られます。
なお、この値は
(問4)
(p と V の関係式を T と V の関係式に変形する)pV γ ポアソンの法則 のことですが、これを定数 k を用いて表現すると、
pV γ k
となり、さらに、ボイル⋅シャルルの法則 を定数 k' を用いて表現すると、
\(\large{\frac{pV}{T}}\) = k'
となり、この2式の辺々を割りますと、
\(\large{\frac{pV^γ}{\frac{pV}{T}}}\) = \(\large{\frac{k}{k'}}\)
\(\large{\frac{V^γ}{\frac{V}{T}}}\) = \(\large{\frac{k}{k'}}\)
∴ TV γ -1
これはつまり、 TV γ -1
(T A と T D を T B 、V A 、V B を用いて表す)*
ポアソンの法則は断熱変化において成り立つものです。
閉じる
T A V A γ -1T B V B γ -1
∴ T A = \(\large{(\frac{V_\rm{B}}{V_\rm{A}}})^{\small{γ-1}}\)T B
C→Dの断熱変化に適用しますと、
T C V C γ -1T D V D γ -1
∴ 2T B (2V B )γ -1T D V A γ -1*
問1より T C = 2T B であり、V C = 2V B であり、V D = V A であり、閉じる
∴ T D = 2×2γ -1T B ×\(\large{(\frac{V_\rm{B}}{V_\rm{A}}})^{\small{γ-1}}\)
= 2γ T B
( γ
(問5)熱効率 ( e = \(\large{\frac{W}{Q_1}}\) = \(\large{\frac{Q_1-Q_2}{Q_1}}\) )は、問2、問3の値を用いて、
e = \(\large{\frac{\frac{R}{2}(3T_{\rm{A}}+5T_{\rm{B}}-3T_\rm{D})}{\frac{5}{2}RT_\rm{B}}}\)
= \(\large{\frac{3T_{\rm{A}}+5T_{\rm{B}}-3T_\rm{D}}{5T_\rm{B}}}\)
= \(\large{\frac{5T_{\rm{B}}-3T_{\rm{D}}+3T_\rm{A}}{5T_\rm{B}}}\)
= 1 - \(\large{\frac{3(T_{\rm{D}}-T_\rm{A})}{5T_\rm{B}}}\) 問4の値を代入すると T B が消去でき
= 1 - \(\large{\frac{3\Big\{2^γ(\frac{V_\rm{B}}{V_\rm{A}})^{\small{γ-1}}-(\frac{V_\rm{B}}{V_\rm{A}})^{\small{γ-1}}\Big\}T_\rm{B}}{5T_\rm{B}}}\)
= 1 - \(\large{\frac{3\Big\{2^γ(\frac{V_\rm{B}}{V_\rm{A}})^{\small{γ-1}}-(\frac{V_\rm{B}}{V_\rm{A}})^{\small{γ-1}}\Big\}}{5}}\)
= 1 - \(\large{\frac{3(2^γ-1)}{5}\big(\frac{V_\rm{B}}{V_\rm{A}}}\big)^{\small{γ-1}}\)
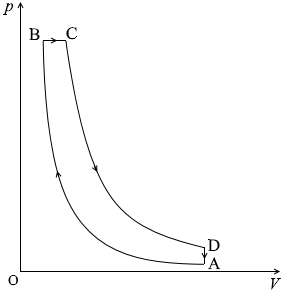
 TD > TA であることはお分かりでしょうか。
TD > TA であることはお分かりでしょうか。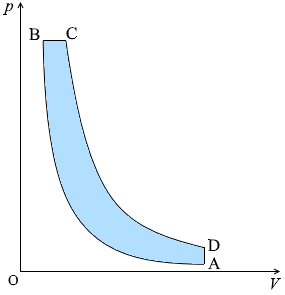 左図の青色部分の面積となっています。
左図の青色部分の面積となっています。