気体の状態変化

変数を固定してみる

理想気体を封入したピストン付きシリンダーにおいて、外部から加えた熱量を \(Q\) [J] 、外部からの仕事を \(W\) [J] 、内部エネルギーの増加分を \(ΔU\) [J] とすると、熱力学第1法則より、

　　　\(ΔU = Q + W\)　　……①

であり、さらに、気体の圧力を \(p\) [Pa] 、体積を \(V\) [m³] 、絶対温度を \(T\) [K] とすると、ボイル⋅シャルルの法則より、

　　　\({\large\frac{pV}{T}}\) = （一定）　　……②

でありますが、

2式の中の様々な変数のうち、どれを固定すると何と何が連動するか、考察してみます。

定積変化

体積が一定のまま、温度や圧力が変化する状態変化を定積変化＊ 定積過程、等積変化、等積過程、定容変化など、いろいろな呼び名があります。 閉じる といいます。これはピストンを固定しながらシリンダーを加熱、冷却するような状態変化です。

\(V\) が一定なので、\(W = pΔV\) の \(ΔV\) が 0 であり、つまり \(W = 0\) であり、①式　\(ΔU = Q\ \color{#bbb}{+\ W}\)　は

　　　\(\boldsymbol{ΔU = Q}\)

となります。ピストンが動かないということは仕事が 0 ということであり、気体に加えられた熱は全て内部エネルギー（=分子のスピード=温度）の増加に使われます。

そして、②式　\({\large\frac{p\color{#bbb}{V}}{T}}\) = （一定） は、\(V\) が一定であるので、

　　　\(\boldsymbol{{\large\frac{p}{T}}}\) = （一定）

となります。圧力と温度が比例するという意味です。

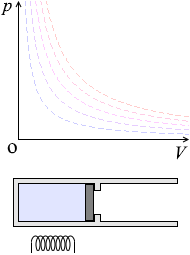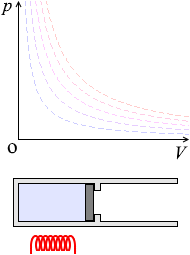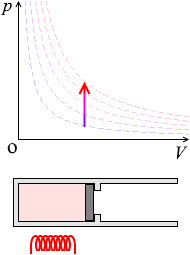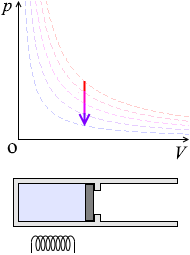要するに、ピストンを固定して加熱すると温度と圧力が上がります。あるいは、冷却すると温度と圧力が下がります。（\(ΔU\) と \(ΔT\) は同じようなものです＊ \(ΔU = {\large\frac{3}{2}}\)\(nRΔT\)　です。
分子の数 \(n\) が変化しない（封入されている気体が漏れたりしない）なら
　\({\large\frac{3}{2}}nR\) は定数であり、
\(ΔU\) と \(ΔT\) は実質的に同じものということになります。 閉じる ）

\(p\textrm{-}V\)グラフにおける定積変化の曲線は縦の線となります。圧力が上がっていくと高温側の等温曲線に移っていきます＊
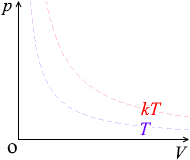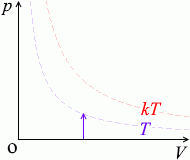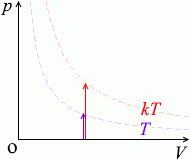
\(p\) が \(k\)倍になると \(T\) も \(k\)倍になります。\({\large\frac{p}{T}}\) =（一定）です。

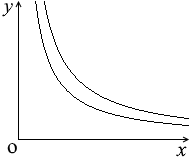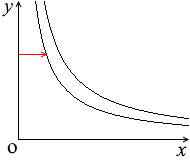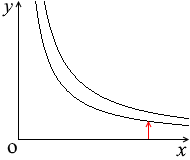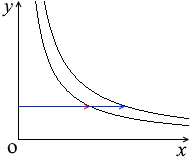数学の直角双曲線の性質の話ですが、たとえば、
\(y={\large\frac{2}{x}}\) の曲線と \(y={\large\frac{3}{x}}\) の曲線を見比べると、どこを切っても1.5倍となっています。 閉じる 。

加熱すると分子のスピードが上がり、すなわち温度が上がり、ピストンと衝突する回数が増え、圧力が上がります。

定圧変化

圧力が一定のまま、温度や体積が変化する状態変化を定圧変化＊ 定圧過程、等圧変化、等圧過程など、いろいろな呼び名があります。 閉じる といいます。これは、ピストンを自由に動けるようにして内圧と外圧が常に等しくなるようにして加熱、冷却するような状態変化です。＊ シリンダーを縦にしてピストンの上に重りを載せれば圧力の大きさを自在に変えられます。（もし外気圧より低い圧力にしたければヘリウム入り風船をピストンに取り付ければいいかもしれません）

閉じる

加熱（ \(Q\) ）すると、分子のスピード（ \(ΔU ≒ ΔT\) ）が上がり、圧力が上がり、ピストンを押して負＊ 今は外部の力がした仕事を \(W\) と定義しているので、気体が膨張した場合は、仕事の正負は「負」です。もし、気体のした仕事を \(W\) と定義してあるならば仕事は「正」で、\(W = pΔV\) です。 閉じる の仕事をし（ \(W = - pΔV\) ）、（体積が増えて分子の衝突回数が元に戻って内圧と外圧が等しくなり）圧力が元に戻り、加熱され、温度が上がり、圧力が上がり、ピストンを押して仕事をし、圧力が元に戻り、加熱され、…、を繰り返します。

①式　\(ΔU = Q + W\)　は

　　　\(\boldsymbol{ΔU = Q - pΔV}\)　　（移項すると \(\boldsymbol{Q = ΔU + pΔV}\) ）

となります。

②式　\({\large\frac{\color{#bbb}{p}V}{T}}\) = （一定） は、\(p\) が一定であるので、

　　　\(\boldsymbol{{\large\frac{V}{T}}}\) = （一定）

となります。体積と温度が比例するという意味です。シャルルの法則のことです。

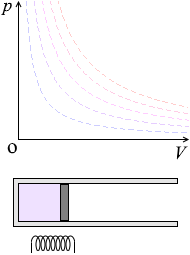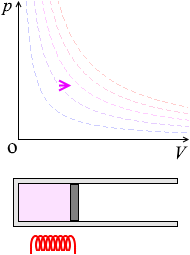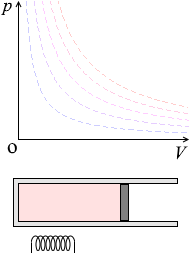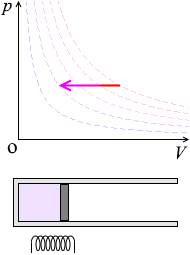ピストンを自由に動けるようにしておいて加熱すると、温度が上がり、体積が増えます。あるいは、冷却すると、温度が下がり、体積が減ります。

\(p\textrm{-}V\)グラフにおける定圧変化の曲線は横の線となります。体積が増えていくと高温側の等温曲線に移っていきます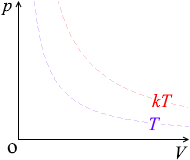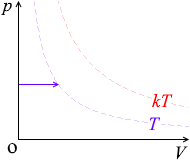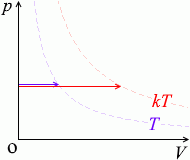＊ \(V\) が \(k\)倍になると \(T\) も \(k\)倍になります。
体積が増えると内部エネルギー（=分子のスピード=温度）が減りそうですが、加熱されているので温度は下がりません。ピストンを強引に引っ張って体積を極端に膨張させれば温度を下げることも可能ですが、今は前提として、内圧と外圧が等しくなるようにピストンは自由に自然に動ける状態にされています。 閉じる 。

加熱すると温度（=分子スピード）が上がり、ピストンと衝突する回数が増え、ピストンを押し、体積が大きくなり、分子が往復する距離が大きくなり、衝突回数が元に戻ります（元の圧力に戻って外部の圧力と等しくなる）。

等温変化

温度が一定のまま、圧力や体積が変化する状態変化を等温変化＊ 定温過程、定温変化、等温過程など、いろいろな呼び名があります。 閉じる といいます。これは、熱を伝えやすい素材でできたシリンダーにおいて、ゆっくりとピストンを動かして常に内部と外部の温度を等しくしておくような状態変化です。

\(T\) が変化しないので \(ΔU = 0\) であり＊ 上の方でも説明しましたが、\(ΔU = {\large\frac{3}{2}}\)\(nRΔT\)　でありますから、\(ΔT = 0\) のとき \(ΔU = 0\) です。 閉じる 、①式　\({\color{#bbb}{ΔU}} = Q + W\)　は

　　　\(\boldsymbol{0 = Q + W}\)

となります。膨張させると外部から熱を奪い（\(W < 0\)、\(Q > 0\) 等温膨張）、圧縮すると外部へ熱を放出します（\(W > 0\)、\(Q < 0\) 等温圧縮）。

②式　\({\large\frac{pV}{\color{#bbb}{T}}}\) = （一定） は、\(T\) が一定であるので、

　　　\(\boldsymbol{pV}\) = （一定）

となります。圧力と体積が反比例するという意味です。ボイルの法則のことです。

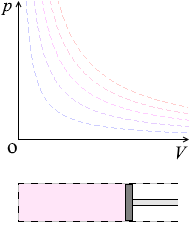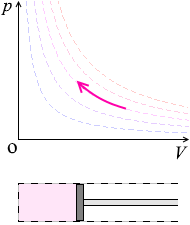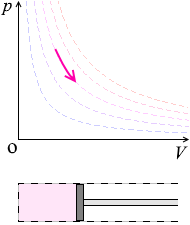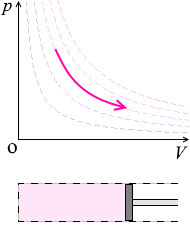温度を一定に保ちながら、ピストンを引くと圧力が下がります。ピストンを押し込むと圧力が上がります。

\(p\textrm{-}V\)グラフにおける等温変化の曲線は等温曲線に沿った線となります。

温度（=分子スピード）を一定に保ちながら体積を大きくすると、ピストンと衝突する回数が減り、圧力が下がります。体積を小さくすると、ピストンと衝突する回数が増え、圧力が上がります。

断熱変化

熱の出入り無しで温度や圧力や体積が変化する状態変化を断熱変化＊ 断熱過程ということもあります 閉じる といいます。これは、断熱素材でできたシリンダーにおいてピストンを動かすような状態変化です。

\(Q\) が 0 なので、①式　\(ΔU = {\color{#bbb}{Q\ +}}\ W\)　は

　　　\(\boldsymbol{ΔU = W}\)

となります。膨張させると温度が下がり（\(W < 0\)、\(ΔU < 0\) 断熱膨張）、圧縮すると温度が上がります（\(W > 0\)、\(ΔU > 0\) 断熱圧縮）。

②式　\({\large\frac{pV}{T}}\) = （一定） は、一定となる変数は無いのでそのまま

　　　\(\boldsymbol{{\large\frac{pV}{T}}}\) = （一定）

です。

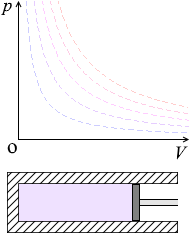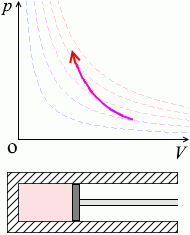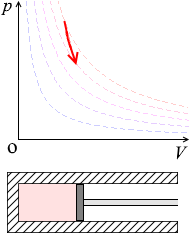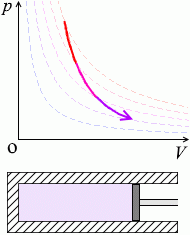断熱された状態で、
ピストンを引く（=体積を大きくする=負の仕事をする）と温度と圧力が下がります。
ピストンを押す（=体積を小さくする=正の仕事をする）と温度と圧力が上がります。

\(p\textrm{-}V\)グラフにおける断熱変化の曲線は等温曲線を次々にまたぎます。

ピストンを外へ引くと、分子のスピードが落ち（=温度が下がる=\(U\)が減少する）、圧力も小さくなり、
ピストンを内へ押すと、分子のスピードが増し（=温度が上がる=\(U\)が増加する）、圧力も大きくなります。

モル比熱

1g の物質の温度を 1K 上げるのに必要な熱量を比熱といいますが、
1mol の物質の温度を 1K 上げるのに必要な熱量をモル比熱といいます。

mol というのは個数のことです。1mol ≒ 602000000000000000000000個 です。この個数の（主に気体）分子の温度を 1K 上げるのに必要な熱量がモル比熱です。物質の種類によりません＊ 単原子分子か二原子分子かには関係があります 閉じる 。比熱は物質の種類によって値が変わります。質量[g]というものは物質の種類によって変わりますが、個数[mol]というものは物質の種類と無関係です。

モル比熱を \(C\) [J/(mol⋅K)] 、気体の物質量を \(n\) [mol] としますと、温度を \(ΔT\) [K] 上げるのに必要な熱量 \(Q\) [J] は

　　　\(\boldsymbol{Q = nCΔT}\)　　……③

となります。（ちなみに比熱の場合は \(Q = mcΔT\) でした）

このモル比熱は、体積一定で加熱する場合と圧力一定で加熱する場合とで2種類の値があります。

定積モル比熱

体積一定のまま、1mol の物質の温度を 1K 上げるのに必要な熱量を定積モル比熱（定積モル熱容量）といいます。

定積変化においては、

　　　\(ΔU = Q\)

であり、気体が単原子分子であれば、

　　　\(ΔU = {\large\frac{3}{2}}nRΔT\)

であるので、

　　　\(Q = {\large\frac{3}{2}}nRΔT\)

となり、定積モル比熱を \(C_{\rm V}\) [J/(mol⋅K)] とすれば、③式　\(Q = nCΔT\)　は以下のようになります。

　　　\({\large\frac{3}{2}}nRΔT = nC_{\rm V}ΔT\)

　∴　\({\large\frac{3}{2}}R = C_{\rm V}\)

\(R\) は定数であるので計算しますと、

　　　\(\boldsymbol{C_{\rm V} = {\large\frac{3}{2}}R = {\large\frac{3}{2}}⋅8.31 ≒ 12.5}\) J/(mol⋅K)

となります。体積一定のまま 1mol の単原子分子の理想気体を 1K 上昇させるには 約12.5J の熱量が必要ということです。

定圧モル比熱

圧力一定のまま、1mol の物質の温度を 1K 上げるのに必要な熱量を定圧モル比熱（定圧モル熱容量）といいます。

定圧変化においては、

　　　\(Q = ΔU + pΔV\)　　……④

であり、気体が単原子分子であれば、

　　　\(ΔU = {\large\frac{3}{2}}nRΔT\)　　……⑤

であり、理想気体の状態方程式より、

　　　\(pΔV = nRΔT\)　　……⑥

であるので、⑤式⑥式を④式に代入すると、

　　　\(Q = {\large\frac{3}{2}}nRΔT + nRΔT\)

　　　　\(= {\large\frac{5}{2}}nRΔT\)

となり、定圧モル比熱を \(C_{\rm p}\) [J/(mol⋅K)] とすれば、③式　\(Q = nCΔT\)　は以下のようになります。

　　　\({\large\frac{5}{2}}nRΔT = nC_{\rm p}ΔT\)

　∴　\({\large\frac{5}{2}}R = C_{\rm p}\)

\(R\) は定数であるので計算しますと、

　　　\(\boldsymbol{C_{\rm p} = {\large\frac{5}{2}}R = {\large\frac{5}{2}}⋅8.31 ≒ 20.8}\) J/(mol⋅K)

となります。圧力一定のまま 1mol の単原子分子の理想気体を 1K 上昇させるには 約20.8J の熱量が必要ということです。

\(C_{\rm p}\) と \(C_{\rm V}\) を比べると、

　　　\(\boldsymbol{C_{\rm p} = C_{\rm V} + R}\)

となっています。マイヤーの関係式といいます＊ 19世紀のドイツの物理学者 ユリウス⋅ロベルト⋅フォン⋅マイヤー が発見しました 閉じる 。定圧モル比熱 \(C_{\rm p}\) は定積モル比熱 \(C_{\rm V}\) より、気体定数\(R\)分だけ大きくなっています。これの由来は \(Q = ΔU + pΔV\) 式 の \(pΔV\) です。ピストンを動かして仕事をした分、比熱も大きくなるのです。気体の温度を上げようとする際、加熱をしてもピストンが動いてしまうと分子のスピードが落ちてしまい、その分、余計に加熱してやらなければならないということです。

比熱比

定圧モル比熱 \(C_{\rm p}\) と定積モル比熱 \(C_{\rm V}\) の比を比熱比といいます。\(γ\)（がんま）で表します＊ なぜ記号に \(γ\) を用いるのかは分かりません 閉じる 。

　　　\(\boldsymbol{γ = {\large\frac{C_{\rm p}}{C_{\rm V}}}}\)

単原子分子の理想気体では、この値は

　　　\(γ = {\large\frac{C_{\rm p}}{C_{\rm V}}} = {\large\frac{\frac{5}{2}R}{\frac{3}{2}R}} = {\large\frac{5}{3}}\) ≒ 1.67

となります。\(γ\) ≒ 1.67 となる気体は単原子分子の気体です。＊ 二原子分子の気体の場合はこの値が \(γ\) = 1.4 となります。

まず、二原子分子の場合は分子1個のエネルギーが
　　\(U = {\large\frac{5}{2}}kT\)
であり、内部エネルギーは
　　\(U = {\large\frac{5}{2}}nRT\)
であり、
　　\(C_{\rm V} = {\large\frac{5}{2}}R\)
であり、
　　\(C_{\rm p} = {\large\frac{5}{2}}R + R = {\large\frac{7}{2}}R\)
であり、
　　\(γ = {\large\frac{C_{\rm p}}{C_{\rm V}}} = {\large\frac{7}{5}}\) = 1.4
となります。

同様にして、三原子分子の場合（非直線型）は、
　　\(γ = {\large\frac{C_{\rm p}}{C_{\rm V}}} = {\large\frac{\frac{8}{2}R}{\frac{6}{2}R}} = {\large\frac{8}{6}}\) ≒ 1.33
となります。

\(γ\) の値が何原子分子であるかの目安になります。

単原子分子の場合も二原子分子の場合も三原子分子の場合もマイヤーの関係式 \(C_{\rm p} = C_{\rm V} + R\) は成り立っています。 閉じる

この比熱比は、断熱変化における \(p\textrm{-}V\)曲線の式にもあらわれ、

　　　\(pV^γ\) = （一定）

となっています。ポアソンの法則といいます＊ 19世紀のフランスの物理学者 シメオン⋅ドニ⋅ポアソン が発見しました。
この式の導出はちょっと難しいです。興味のある方は「ポアソンの法則」で検索してみてください。 閉じる 。単原子分子であるならば　\(pV^{1.67}\) = （一定） です。等温変化の \(p\textrm{-}V\)曲線の式　\(pV\) = （一定） よりも曲線の角度が急になります＊ 　\(pV = k\) の曲線と \(pV^{1.67} = k\) の曲線。

\(V\) が 1 より小さいとき、\(p\) より \(p\) の方が大きい。
\(V\) が 1 のとき、\(p\) = \(p\) = \(k\) 。
\(V\) が 1 より大きいとき、\(p\) より \(p\) の方が小さい。 閉じる 。