qOCC3　■わかりやすい高校物理の部屋■

次の文章を読み、後の問い（問1～5）に答えよ。

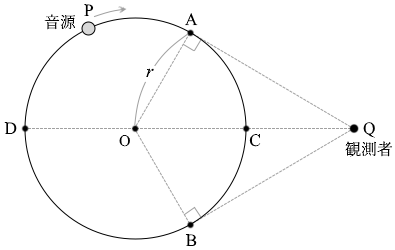
　全方向に等しく音を出す小球状の音源が、図1のように、点Oを中心として半径 \(r\) 、速さ \(v\) で時計回りに等速円運動をしている。音源は一定の振動数 \(f_0\) の音を出しており、音源の円軌道を含む平面上で静止している観測者が、届いた音波の振動数 \(f\) を測定する。
　音源と観測者の位置をそれぞれ点P、Qとする。点Qから円に引いた2本の接線の接点のうち、音源が観測者に近づきながら通過する方を点A、遠ざかりながら通過する方を点Bとする。また、直線OQが円と交わる2点のうち観測者に近い方を点C、遠い方を点Dとする。\(v\) は音速 \(V\) より小さく、風は吹いていない。

（問1）音源にはたらいている向心力の大きさと、音源が円軌道を点Cから点Dまで半周する間に向心力がする仕事を表す式の組合せとして正しいものを、次の①～⑤のうちから一つ選べ。ただし、音源の質量を \(m\) とする。

	①	②	③	④	⑤
向心力の大きさ	\(mrv^2\)	\(mrv^2\)	0	\(\Large\frac{mv^2}{r}\)	\(\Large\frac{mv^2}{r}\)
仕事	\(π\ mr^2v^2\)	0	0	\(π\ mv^2\)	0

（問2）次の文章中の空欄17に入れる語句として最も適当なものを、直後の｛｝で囲んだ選択肢のうちから一つ選べ。

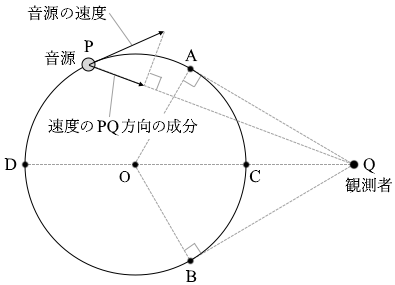
音源の等速円運動にともなって \(f\) は周期的に変化する。これは、音源の速度の直線PQ方向の成分によるドップラー効果が起こるからである（図2）。このことから、\(f\) が \(f_0\) と等しくなるのは、音源が
17｛ ① A 　② B 　③ C 　④ D 　⑤ AとB 　⑥ CとD 　⑦ A、B、C、D ｝を通過したときに出した音を測定した場合であることがわかる。

（問3）音源が点A、点Bを通過したときに出した音を観測者が測定したところ、振動数はそれぞれ \(f_{\rm A}\) 、\(f_{\rm B}\) であった。\(f_{\rm A}\) と音源の速さ \(v\) を表す式の組合せとして正しいものを、次の①～⑥のうちから一つ選べ。

	①	②	③	④	⑤	⑥
\(f_{\rm A}\)	\(f_0\)	\(f_0\)	\({\Large\frac{V+v}{V}}f_0\)	\({\Large\frac{V+v}{V}}f_0\)	\({\Large\frac{V}{V-v}}f_0\)	\({\Large\frac{V}{V-v}}f_0\)
\(v\)	\({\Large\frac{f_{\rm B}}{f_{\rm A}}}V\)	\({\Large\frac{f_{\rm A}-f_{\rm B}}{f_{\rm A}+f_{\rm B}}}V\)	\({\Large\frac{f_{\rm B}}{f_{\rm A}}}V\)	\({\Large\frac{f_{\rm A}-f_{\rm B}}{f_{\rm A}+f_{\rm B}}}V\)	\({\Large\frac{f_{\rm B}}{f_{\rm A}}}V\)	\({\Large\frac{f_{\rm A}-f_{\rm B}}{f_{\rm A}+f_{\rm B}}}V\)

次に、音源と観測者を入れかえた場合を考える。図3に示すように、音源を点Qの位置に固定し、観測者が点Oを中心に時計回りに等速円運動をする。

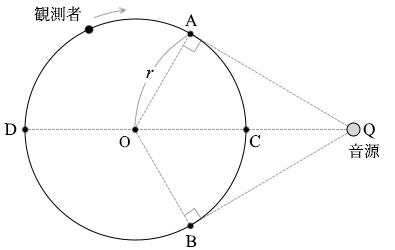
（問4）このとき、等速円運動をする観測者が測定する音の振動数についての記述として最も適当なものを、次の①～⑤のうちから一つ選べ。

① 点Aにおいて最も大きく、点Bにおいて最も小さい。
② 点Bにおいて最も大きく、点Aにおいて最も小さい。
③ 点Cにおいて最も大きく、点Dにおいて最も小さい。
④ 点Dにおいて最も大きく、点Cにおいて最も小さい。
⑤ 観測の位置によらず、常に等しい。

音源が等速円運動している場合（図1）と観測者が等速円運動している場合（図3）の音の速さや波長について考える。

（問5）次の文章(a)～(d)のうち、正しいものの組合せを、後の①～⑥のうちから一つ選べ。

(a) 図1の場合、観測者から見ると、点Aを通過したときに出した音の速さの方が、点Bを通過したときに出した音の速さより大きい。
(b) 図1の場合、原点Oを通過する音波の波長は、音源の位置によらずすべて等しい。
(C) 図3の場合、音源から見た音の速さは、音が進む向きによらずすべて等しい。
(d) 図3の場合、点Cを通過する音波の波長は、点Dを通過する音波の波長より長い。

①　(a)と(b)　 ②　(a)と(c)　 ③　(a)と(d)　 ④　(b)と(c)　 ⑤　(b)と(d)　 ⑥　(c)と(d)

#共テ23本試物理

（問1）
質量 \(m\) の物体が半径 \(r\) の円を速さ \(v\) で等速円運動しているときの向心力の大きさは \(\Large\frac{mv^2}{r}\) です。

向心力の向き（＝加速度の向き）は常に円の中心を向いています。移動の向きとは直角をなしています。そして移動の向きと力の向きが直角のときというのは、仕事は 0 です。（向きが違う例参照）

答えは ⑤ です。

（問2）
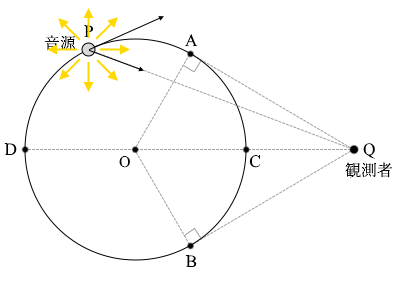音源が接線方向に進んでいるからといってそちら方向に向かって音が出ているわけではなく、問題文にあるように360°全方向に音が出ているわけですが、

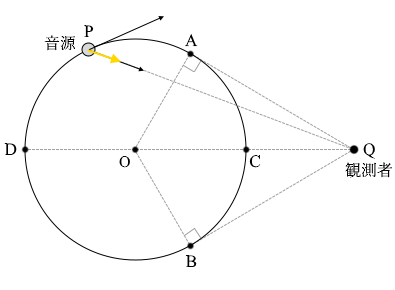そのうちの点Qを向く方向の音が観測者に届きます。

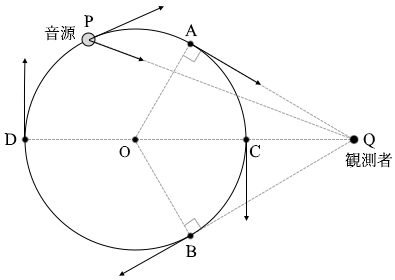そしてこの音は、速度のPQ方向の成分の速さで観測者に近づいていて、そのためドップラー効果が起こります。

速度のPQ方向の成分というのは、
点Aを通過するときは音源の速度と一致し、最大で、
点Cでは 0、
点Bでは遠ざかる方向で最大、
点Dでは 0、
となります。

\(f\) と \(f_0\) が等しくなるのはドップラー効果が起こらないということであり、音源が観測者に近づきもせず遠ざかりもしない瞬間です。答えは ⑥ CとD です。

（問3）
ドップラー効果の式に各量を当てはめて \(f_{\rm A}\) 、\(f_{\rm B}\) を求めますと、

　　\(f_{\rm A} = {\large\frac{V-0}{V-v}}f_0 = \textcolor{yellow}{\underline{\textcolor{black}{{\large\frac{V}{V-v}}f_0}}}\)

　　\(f_{\rm B} = {\large\frac{V-0}{V-(-v)}}f_0 = {\large\frac{V}{V+v}}f_0\)

問題の表で示された \(v\) の①～⑥の選択肢を見ると \(f_0\) が含まれてません。上2式から \(f_0\) を消去して \(v\) を求めます。

　上の \(f_{\rm A}\) の式を変形しますと、

　　\(f_{\rm A}(V-v) = Vf_0\)

　同じく \(f_{\rm B}\) の式を変形しますと、

　　\(f_{\rm B}(V+v) = Vf_0\)

よって

　　\(f_{\rm A}(V-v) = f_{\rm B}(V+v)\)

∴　\(-f_{\rm A}v - f_{\rm B}v = - f_{\rm A}V + f_{\rm B}V\)

∴　\(- (f_{\rm A} + f_{\rm B})v = - (f_{\rm A} - f_{\rm B})V\)

∴　\(v = \textcolor{yellow}{\underline{\textcolor{black}{{\Large\frac{f_{\rm A}-f_{\rm B}}{f_{\rm A}+f_{\rm B}}}V}}}\)

答えは ⑥ です。

（問4）
振動数が大きくなったり小さくなったりするのはドップラー効果のせいですが、音源が動く場合でも観測者が動く場合でも、お互いに近づくスピードが大きいほど振動数は大きくなり、遠ざかるスピードが大きいほど振動数は小さくなります。

問2で説明したように、点Aを通過する瞬間が近づくスピードが最大で、点Bを通過する瞬間が遠ざかるスピードが最大です。点C、点Dではドップラー効果は起こりません。

答えは ① 点Aにおいて最も大きく、点Bにおいて最も小さい。です。

（問5）

(a) 図1の場合、観測者から見ると、点Aを通過したときに出した音の速さの方が、点Bを通過したときに出した音の速さより大きい。

音波というものは加速できません。気温が一定なら音波の速さは一定です。

(b) 図1の場合、原点Oを通過する音波の波長は、音源の位置によらずすべて等しい。

そのとおりです。音源と原点Oの距離は常に一定です。ドップラー効果も起こりませんし、振動数も波長も変化しません。

そのとおりです。(a)で説明したとおり音の速さというものは一定です。そもそも図3では音源は静止しています。この選択肢は何がいいたいのかちょっとよくわかりません。

(d) 図3の場合、点Cを通過する音波の波長は、点Dを通過する音波の波長より長い。

波長は長くなりません。音波の速さが一定で、ドップラー効果が起こらない、すなわち振動数も一定です。そうであれば波長も一定です。

答えは ④ (b)と(c) です。