qH2EA

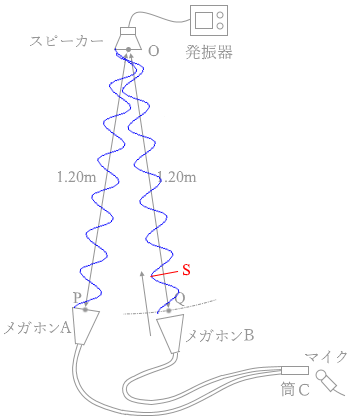
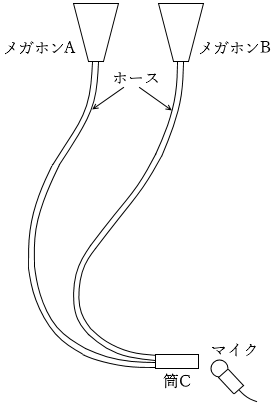
図2のように、同じ大きさのプラスチック製の筒（メガホン）を二つ用意し、それぞれメガホンA、Bとする。メガホンA、Bの小さな開口部に、同じ長さで同じ太さのホースを接続し、ホースの他端を束ねて筒Cに接続する。メガホンA、Bの大きな開口部に入った音は、筒Cで重ね合わさり、筒Cの開口部から出て来る。筒Cの開口部の近くにマイクを置き、出て来た音の大きさを測定する。ただし、メガホンは十分に広い角度から来る音を拾うように作られているとする。

図 2

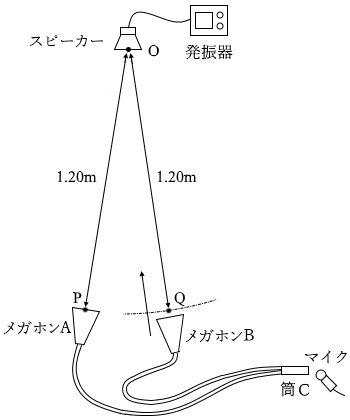
（問3）図3のように、スピーカーを点Oに置き振動数が 1700Hz の音を出す。メガホンAを点Oから 1.20m の点Pに固定し、メガホンBを点Oから 1.20m より少し離れた位置に置く。この位置からメガホンBをゆっくり点Oに向かって近づけていったところ、筒Cから出て来る音が次第に大きくなり、点Oから 1.20m の点Qを過ぎると、逆に音が小さくなっていった。さらにメガホンBを点Oに向かって近づけていくと、ある点Rから再び音が大きくなりはじめた。距離ORはいくらか。ただし、音速を 340m/s とする。

図 3

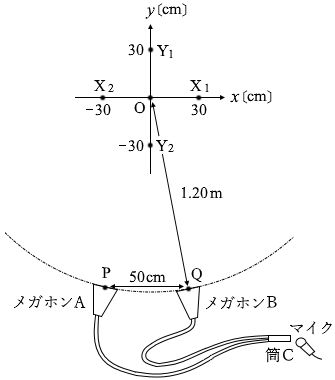
（問4）次に、図4のように、メガホンA、Bの位置を点Oから 1.20m の点P、Qに固定した。PQ間の距離は 50cm とする。点Oを原点として、PQに平行に x軸をとり、x軸に垂直に y軸をとる。原点Oから 30cm の距離にある x、 y軸上の点を、それぞれ、点X1、X2、Y1、Y2とする。また、スピーカー、点P、Q、および、x、y軸は、常に同一平面上にあるとする。
1700Hz の音を出すスピーカーの位置を少しずつ変え、それぞれの位置で筒Cから出て来る音の大きさの変化を調べた。スピーカーの位置を x軸に沿って点X1から点X2に徐々に変えた場合と、y軸に沿って点Y1から点Y2に徐々に変えた場合の筒Cから出て来る音の大きさの記述の組合せとして最も適当なものを、下の①～⑨のうちから一つ選べ。

図 4
点X1 → 点X2 点Y1 → 点Y2
① 原点Oで最小となる。 原点Oで最小となる。
② 原点Oで最小となる。 原点Oで最大となる。
③ 原点Oで最小となる。 徐々に大きくなる。
④ 原点Oで最大となる。 原点Oで最小となる。
⑤ 原点Oで最大となる。 原点Oで最大となる。
⑥ 原点Oで最大となる。 徐々に大きくなる。
⑦ 変わらない。 原点Oで最小となる。
⑧ 変わらない。 原点Oで最大となる。
⑨ 変わらない。 徐々に大きくなる。

#センター13本試

（問3）
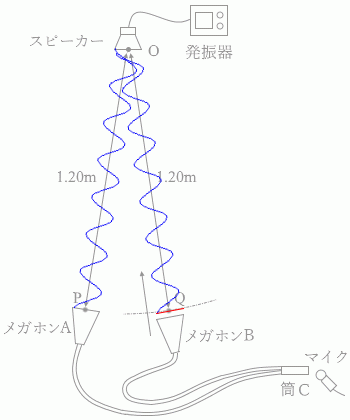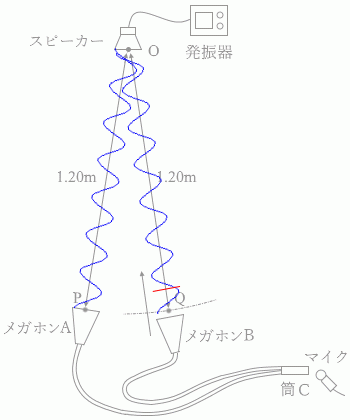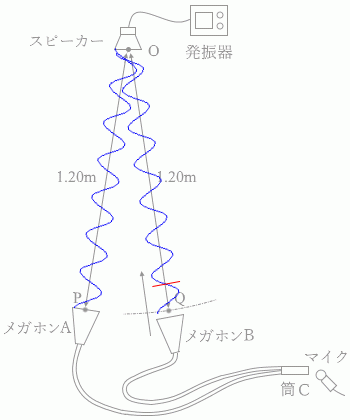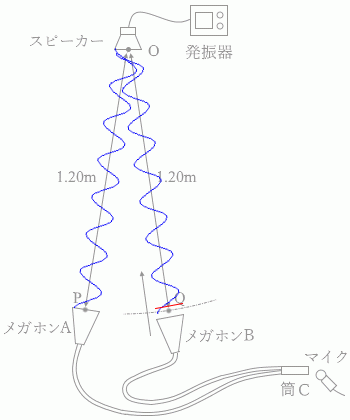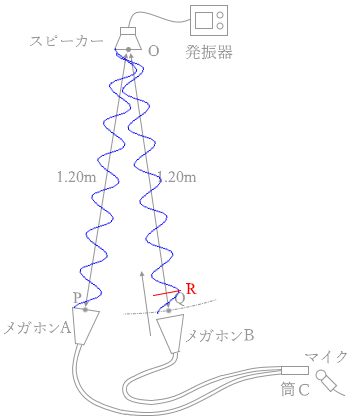メガホンAとメガホンBがそれぞれ点P、点Qにあるときは、音波の位相が揃っているので音が大きく聞こえます。（『音の干渉』、『干渉の条件』参照）

メガホンBが半波長分ズレた位置にあれば、波が打ち消し合って音が小さく聞こえます。この位置が点Rです。
メガホンBが点Sの位置に来れば、
再び音は大きくなります。

この音波の波長 λ を求めます。
振動数が 1700Hz で速さが 340m/s だから、波の基本式（v = fλ）より、

　　　　λ = \(\large{\frac{340}{1700}}\) = 0.20 [m]

この半分の 0.10m がQRの長さであり、求めるORの長さは

　　　　OR = 1.20 - 0.10 = 1.10 [m]

　

　

（問4）
（点X1 → 点X2）
問3で説明したように、スピーカーが原点Oにあれば、点P、点Qに届く2つの波は位相が揃うので強め合い、音は大きくなります。スピーカーがそれ以外の位置にあるときは位相が揃うとは限らないので、音の大きさは原点Oのとき以下となります。

（点Y1 → 点Y2）
スピーカーの位置が点Y1でも、原点Oでも、点Y2でも、点P、点Qに届く2つの波は位相が揃うので強め合い、音は大きくなります。なおかつ、音というものは近くに音源があるときの方が大きくなりますから、点Y1にあるときより点Y2にあるときの方が音は大きくなります。 問3の説明において、音波を

このように描いてしまいましたが（レーザーなど減衰しない波ならこれでいいかもしれませんが）、
厳密には

このようであると考えるべきです。

というわけで答えは ⑥ です。

↑ ↓