（問1）
波の基本式より、
f = \(\large{\frac{1}{T}}\)
λ = \(\large{\frac{v}{f}}\) = vT
（問2）
「x軸上の原点Oでの媒質の変位は時刻 t の関数として y = Asin\(\large{\frac{2π}{T}}\)t で表される」ということなので、この波は正弦波であり、正弦波にもいろいろな場合がありますが、これはノーマルな場合であり、x < L における変位を y1 と置くと、『正弦波の式』で説明したように、
y1 = Asin\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{x}{v}}\)\(\big)\)
（問3）
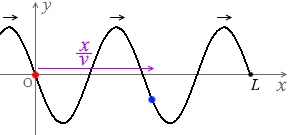上の式は y = Asin\(\large{\frac{2π}{T}}\)t の式の t の部分に \(\big(\)t - \(\large{\frac{x}{v}}\)\(\big)\) を代入して求めたわけですが、
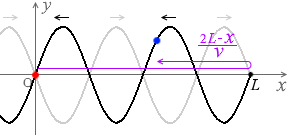今度は、x の地点まで波が進むのに
\(\large{\frac{L+(L-x)}{v}}\) = \(\large{\frac{2L-x}{v}}\)
だけ時間が掛かるので、
t の部分に \(\big(\)t - \(\large{\frac{2L-x}{v}}\)\(\big)\) を代入しなければなりません。
なおかつ、固定端反射をするので位相が π ズレます。位相が π ズレるということは sin の中身に π を足すということであり、正負が逆になるということです
sin(θ ± π) = - sinθ です。
詳しくは数学の教科書を見てください。
上のグラフの曲線を見てもわかると思います。
グレー色の波と黒色の波は正負が逆転しています。
。
つまり、反射波の変位を y2 と置くと、
y2 = - Asin\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{2L-x}{v}}\)\(\big)\)
（問4）
入射波と反射波が重なり合った合成波の変位を y3 としますと、
y3 = y1 + y2
= Asin\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{x}{v}}\)\(\big)\) - Asin\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{2L-x}{v}}\)\(\big)\)
= A\(\Big\{\)sin\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{x}{v}}\)\(\big)\) - sin\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{2L-x}{v}}\)\(\big)\)\(\Big\}\)
= A\(\Bigg[\)2sin\(\large{\frac{2π}{T}}\)⋅\(\large{\frac{1}{2}}\)⋅\(\Big\{\)\(\big(\)t - \(\large{\frac{x}{v}}\)\(\big)\) - \(\big(\)t - \(\large{\frac{2L-x}{v}}\)\(\big)\)\(\Big\}\)cos\(\large{\frac{2π}{T}}\)⋅\(\large{\frac{1}{2}}\)⋅\(\Big\{\)\(\big(\)t - \(\large{\frac{x}{v}}\)\(\big)\) + \(\big(\)t - \(\large{\frac{2L-x}{v}}\)\(\big)\)\(\Big\}\)\(\Bigg]\)
（ ∵ 和積の公式 sinα ± sinβ = 2sin\(\large{\frac{α±β}{2}}\)cos\(\large{\frac{α∓β}{2}}\) ）
= A\(\Bigg[\)2sin\(\large{\frac{2π}{T}}\)⋅\(\large{\frac{1}{2}}\)⋅\(\Big\{\) - \(\large{\frac{x}{v}}\) + \(\large{\frac{2L-x}{v}}\)\(\Big\}\)cos\(\large{\frac{2π}{T}}\)⋅\(\large{\frac{1}{2}}\)⋅\(\Big\{\)2t - \(\large{\frac{x}{v}}\) - \(\large{\frac{2L-x}{v}}\)\(\Big\}\)\(\Bigg]\)
= A\(\Bigg[\)2sin\(\large{\frac{2π}{T}}\)⋅\(\large{\frac{1}{2}}\)⋅\(\Big\{\)\(\large{\frac{2L-2x}{v}}\)\(\Big\}\)cos\(\large{\frac{2π}{T}}\)⋅\(\large{\frac{1}{2}}\)⋅\(\Big\{\)2t - \(\large{\frac{2L}{v}}\)\(\Big\}\)\(\Bigg]\)
= A\(\Bigg[\)2sin\(\large{\frac{2π}{T}}\)\(\Big\{\)\(\large{\frac{L-x}{v}}\)\(\Big\}\)cos\(\large{\frac{2π}{T}}\)\(\Big\{\)t - \(\large{\frac{L}{v}}\)\(\Big\}\)\(\Bigg]\)
= 2Asin\(\large{\frac{2π}{T}}\)\(\big(\)\(\large{\frac{L-x}{v}}\)\(\big)\)cos\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{L}{v}}\)\(\big)\)
よって、波形を表す sin\(\large{\frac{2π}{T}}\)\(\big(\)\(\large{\frac{L-x}{v}}\)\(\big)\) の位相 \(\large{\frac{2π}{T}}\)\(\big(\)\(\large{\frac{L-x}{v}}\)\(\big)\) が各点ごとに一定なので定常波となる。
（どういうことかといいますと、）
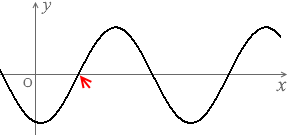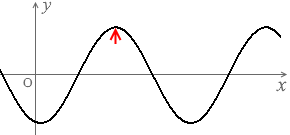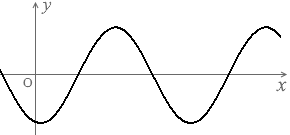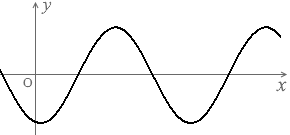位相というのは、波の1周期のうちのどのタイミングであるかを示す量ですが、
波が進行するということは、この位相が変化するということです。
上式の sin の中身の \(\large{\frac{2π}{T}}\)\(\big(\)\(\large{\frac{L-x}{v}}\)\(\big)\) は位相を表してますが、これは x が定められていれば変化しない値です。
たとえば、
x = x1 のときは \(\large{\frac{2π}{T}}\)\(\big(\)\(\large{\frac{L-x_1}{v}}\)\(\big)\) という定数で、
x = x2 のときは \(\large{\frac{2π}{T}}\)\(\big(\)\(\large{\frac{L-x_2}{v}}\)\(\big)\) という定数です。
その地点においては位相が変化しないということです。
たしかに、t が増減すれば cos\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{L}{v}}\)\(\big)\) も増減しますが、
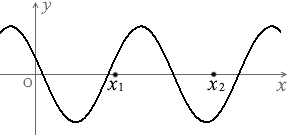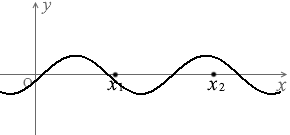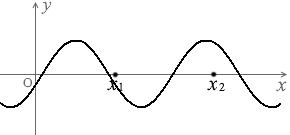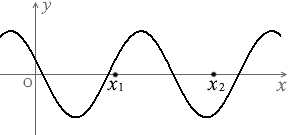これは位相が変化するわけではなく振幅が変化するだけです。
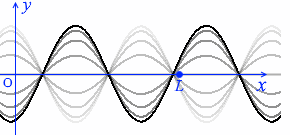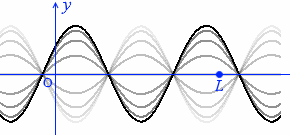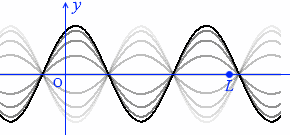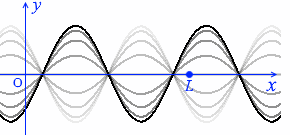
左図の x1点、x2点は、振幅は変化していますが位相は変化していません。（正確にいえば、半周期ごとの位相が変化していません。半周期ごとに位相が π ズレます。変位の正負が入れ替わります。これは cos\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{L}{v}}\)\(\big)\) によるものです。）
問2の式
y1 = Asin\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{x}{v}}\)\(\big)\)
は sin の中に t も x もありましたが、
y3 = 2Asin\(\large{\frac{2π}{T}}\)\(\big(\)\(\large{\frac{L-x}{v}}\)\(\big)\)cos\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{L}{v}}\)\(\big)\)
という式は x と t が sin と cos とに別れています。このようなときは波は進行しません。
（さらに、たとえば）
時刻 t を固定すると上式の cos\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{L}{v}}\)\(\big)\) の部分は定数となり、これを C と置けば、
y3 = 2Asin\(\large{\frac{2π}{T}}\)\(\big(\)\(\large{\frac{L-x}{v}}\)\(\big)\)⋅C
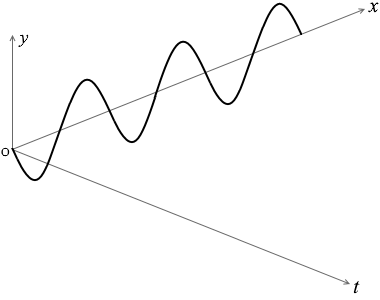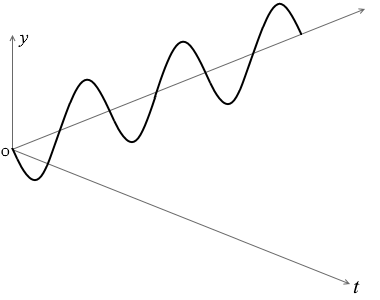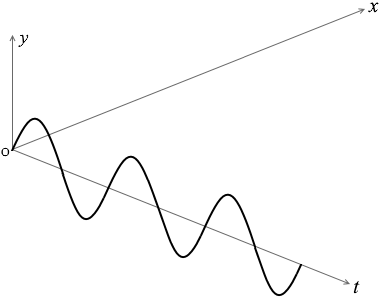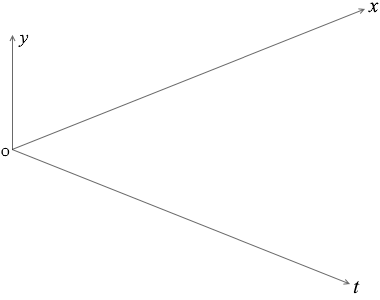
と表現でき、これは y-tグラフの曲線を表します。
一方、場所 x を固定すると sin\(\large{\frac{2π}{T}}\)\(\big(\)\(\large{\frac{L-x}{v}}\)\(\big)\) の部分が定数となり、これを S と置けば、
y3 = 2A⋅S⋅cos\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{L}{v}}\)\(\big)\)
と表現でき、これは y-xグラフの曲線を表します。
『横軸が x か t か』参照。
（問5）
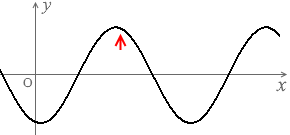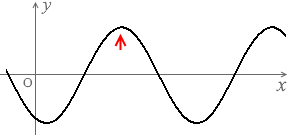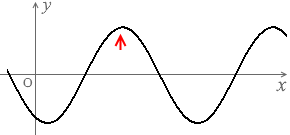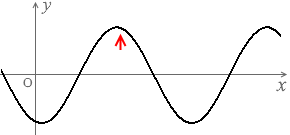
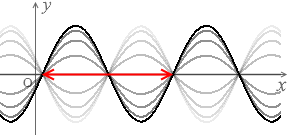定常波の1波長は左図の赤矢印のような長さであり、
L の長さはその \(\large{\frac{5}{4}}\) 倍ということであり、
L の位置は固定端であるので節になるはずなので、
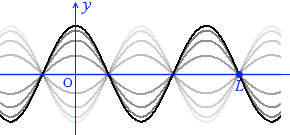このようになるはずです。
そして、問4の
y3 = 2Asin\(\large{\frac{2π}{T}}\)\(\big(\)\(\large{\frac{L-x}{v}}\)\(\big)\)cos\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{L}{v}}\)\(\big)\)
という式の sin\(\large{\frac{2π}{T}}\)\(\big(\)\(\large{\frac{L-x}{v}}\)\(\big)\) の部分と cos\(\large{\frac{2π}{T}}\)\(\big(\)t - \(\large{\frac{L}{v}}\)\(\big)\) の部分のそれぞれの最大値は + 1 で、最小値は - 1 であるので
- 1 ≦ sinθ ≦ 1 、
- 1 ≦ cosθ ≦ 1 です。
、
y3 の最大値は + 2A で、最小値は - 2A であり、
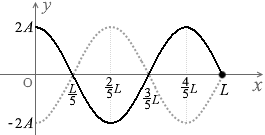概略図は左図のようになります。