図1のように、発振器につながれた二つのスピーカーAおよびBを、十分離して向かい合わせに置き、振動数 f0 の音を発生させた。音速を V とし、風は吹いていないものとする。
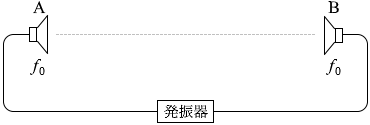
（問1）スピーカーA、Bの間で、図1の破線に沿って音の干渉を観測したところ、音が最も強めあう点が等間隔 L で存在した。L を式で表わせ。
（問2）次の文章中の空欄ア・イに入る式を示せ。
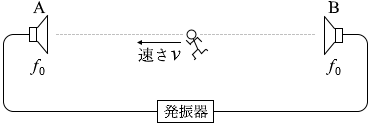
図2のように、観測者がスピーカーBからAに向かって破線上を一定の速さ v (v < V ) で動いたところ、観測者がAとBから受ける音の振動数がそれぞれ f0 から変化し、観測者にはうなりが聞こえた。このとき、観測者がAから受けた音の振動数はアである。また、単位時間あたりのうなりの回数はイである。このうなりは、音が強めあう場所と弱めあう場所を、交互に観測者が通過することにより聞こえると考えることもできる。
#センター16本試物理
（問1）
左右から同じ波がやってくると定常波ができますが、強めあう点というのは定常波の腹の部分のことです。（節の部分では音が消える
ノイズキャンセリングの原理です。
）。そして腹と腹の間隔は波長の半分です。
波長というのは速さを振動数で割ったものであり、
\(\large{\frac{V}{f_0}}\)
これを半分にしたものが L であり、
L = \(\large{\frac{V}{2f_0}}\)
（問2）
ア
ドップラー効果の公式 f = \(\large{\frac{V-v_{\rm{o}}}{V-v_{\rm{s}}}}\)f0 に各量を代入しますと、
観測者がAから受けた音の振動数（ fA と置く）は
fA = \(\large{\frac{V+v}{V}}\)f0
観測者がBから受けた音の振動数（ fB と置く）は
fB = \(\large{\frac{V-v}{V}}\)f0
イ
観測者には fA と fB の音が聞こえ、その差がうなりの振動数（=単位時間あたりのうなりの回数）となるから、
| fA - fB | = \(\large{\frac{V+v}{V}}\)f0 - \(\large{\frac{V-v}{V}}\)f0 = \(\large{\frac{2v}{V}}\)f0
（余談）
問題文に「このうなりは、音が強めあう場所と弱めあう場所を、交互に観測者が通過することにより聞こえると考えることもできる。」とありますが、これに関しては qGACD の解説をご覧ください。