電流が磁場から受ける力
電流が磁場から受ける力の大きさ
『フレミングの左手の法則』項で、磁場の中を流れる電流が受ける電磁力の向きについて説明しましたが、本項ではその力の大きさについて説明します。
一様な磁場の中に、磁場と垂直な向きに導線が置かれているとします。導線に流れる電流の大きさを I [A] 、磁場の強さを H [A/m] 、導線の長さを l [m] とすると、導線を流れる電流が受ける力の大きさ F [N] は、
F = μIHl
となります。電流の大きさ、磁場の強さ、導線の長さに比例するのです。
μ（ミュー）は 透磁率と呼ばれる量で、導線のまわりの物質の種類＊上図では空気のことです。空気以外の場所で実験すると μ の値が変わり、力の掛かり具合も変わります。
閉じるによって変わります。磁化しやすい物質ほど値が大きくなります。下で説明します。
導線が磁場に垂直に置かれた場合の電磁力の大きさは上式で表されますが、導線が磁場に対して斜めに置かれた場合は電磁力は小さくなってしまいます。
磁場と導線との角度が θ としますと、上式は以下のように書き換えられます。
電流が磁場から受ける力
F = μIHlsinθ
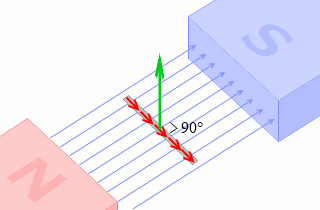θ=90° のときは sin90° = 1 ですので、
F = μIHlsinθ = μIHlsin90° = μIHl
であり、これは、磁場と導線とが垂直のときは力が最大になる、ということです。
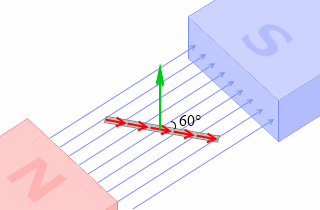他にたとえば、θ=60° のときは sin60° = \(\large{\frac{\sqrt{3}}{2}}\) ≒ 0.87 ですので、
F = μIHlsinθ = μIHlsin60° = 0.87×μIHl
であり、垂直の場合に比べると少し小さくなります。
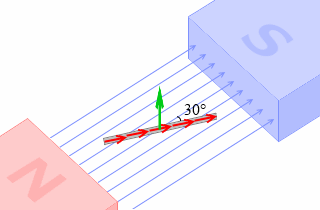さらにたとえば、θ=30° のときは sin30° = \(\large{\frac{1}{2}}\) ですので、
F = μIHlsinθ = μIHlsin30° = \(\large{\frac{1}{2}}\)μIHl
であり、垂直のときと比べると力が半分になってしまうということです。
θ=0° のときは sin0° = 0 ですので、F = μIHlsinθ = μIHlsin0° = 0 です。磁場と電流が平行なときは力を受けないということです。＊電流と電流が平行なときは力を受けます。
閉じる
（これらの計算は大学で習う”外積”という計算になっています。これに対して『力の向きと移動の向きが異なるときの仕事』の Fscosθ という計算は”内積”とよばれる計算です。詳しくは「内積 外積」で検索して調べてみてください。）
F = μIHlsinθ という式は、磁束密度 B というものを用いて F = IBlsinθ とも書き表されます。
電流が磁場から受ける力
F = IBlsinθ
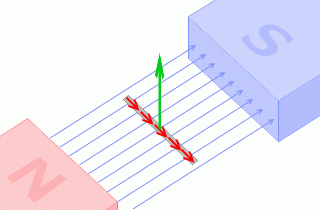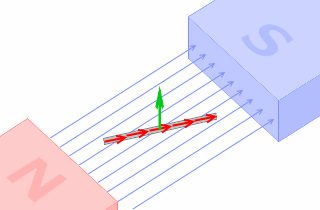
磁場と導線との角度 θ はミスしやすい
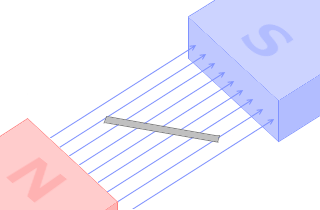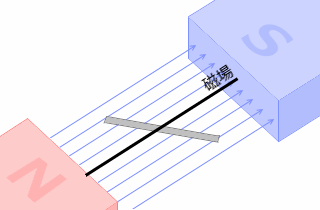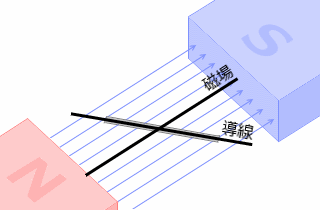
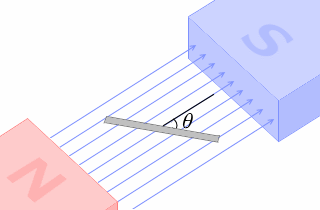磁場と導線との角度といったら左図のような角度のことです。
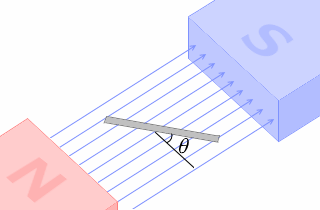決して左図のような角度のことではありません。
これは非常に間違いやすいです。問題を解くときは十分注意してください。
