自己誘導

自己誘導の原理

ループ状の回路において、電流を増減させると、磁場の強さも変化し、その磁場の変化による電磁誘導によって、もともとの電流の変化を妨害する方向に誘導起電力（逆起電力）が発生します。これを自己誘導といいます。

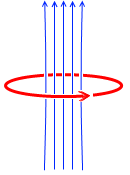電流を流すと磁場が発生します。

このとき電流が一定なら何も起こりませんが、

電流が変化すると、

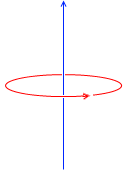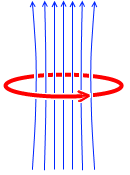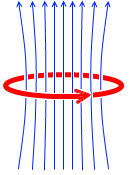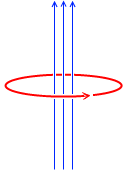磁場も変化し、

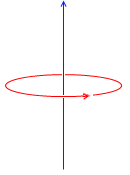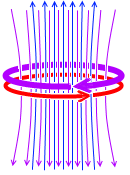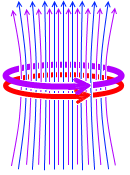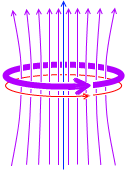
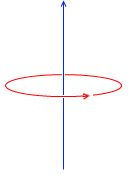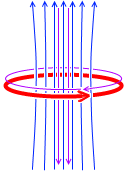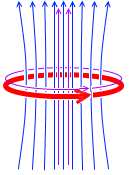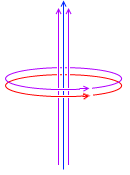磁場が変化すると電磁誘導が起こります。これが自己誘導です。左図の円形の紫色矢印のことです。

自己誘導によって磁場の増加を打ち消すような方向に自己誘導起電力が発生します。増える過程では減らすように、減る過程では増やすように、発生します。（ 右ねじの法則、レンツの法則 ）。電流の変化を打ち消そうとする向きです。自己誘導は電流の急激な変化を和らげる作用があります。変化してないときは発生しません。

変化が急なときは、自己誘導起電力が大きくなります。

左図の青色矢印の磁場を順磁場、紫色矢印の磁場を仮想対抗磁場とでも名付けるとすると、順磁場の変化が急なときに仮想対抗磁場が大きくなります。

電流の変化 → 磁場の変化 → 電磁誘導 → 逆起電力
これが自己誘導 です。

コイルを含む回路に流れる電流

自己誘導現象がはっきり現れる回路部品がコイル＊コイルは 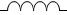という記号が用いられることも多いです。
自己誘導を目的としたコイルはインダクタと呼ばれたりします。
　閉じるで、

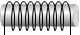それをさらに強力にするために鉄心を挿入した回路部品をチョークコイルといいます。

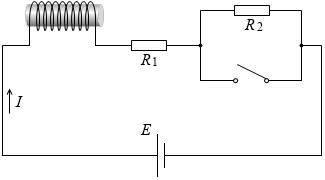左図のような回路について考えてみます。

＊なぜこのような回路を例示するかといいますと、
　
　
　
　
　
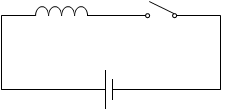このような回路では電流が流れすぎて焼け焦げてしまい、
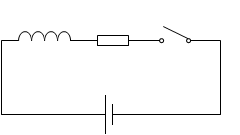抵抗器を取り付ければいいのですが、でもしかし、このような回路ではスイッチを切ったとたんに電流が 0 になって、自己誘導の影響を観測できなくなってしまいます。
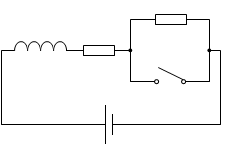ですので、このような回路が適当というわけです。これならスイッチを切っても電流が流れ続けます。
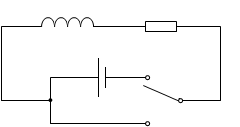このような回路でもいいかもしれませんが、これだとスイッチを入れ替えるときに、一瞬、電流が 0 になってしまうのであまりよくありません。
　 閉じる

電池の内部抵抗を無視しますと、スイッチが開いているときは、回路には、

　　　　I = \(\large{\frac{E}{R_1+R_2}}\)

の大きさの電流が流れています。スイッチを閉じると抵抗が小さくなって、電流が大きくなり、

　　　　I = \(\large{\frac{E}{R_1}}\)

となります。

スイッチを閉じた瞬間、電流が大きくなるのですから、コイル内の磁場が大きくなり、そのことによって電磁誘導が起こり、もともと流れている電流と反対方向に誘導起電力が発生し（自己誘導）、電流の増加を妨害します＊チョークコイルの choke は「詰まらせる」という意味です。チョークスリーパー、ギロチンチョークのチョークです。
（黒板に字を書くときのチョーク chalk は石灰岩のことです。）
　閉じる。しかしこの妨害はずっと続くわけではなく、磁場の変化量が小さくなるにつれて誘導起電力も小さくなり、やがて 0 になります。つまり妨害は止みます。（実際にはここまでの動作は一瞬のうちに終了します。）

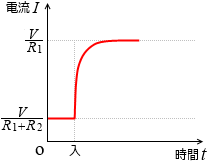このときの電流の大きさの変化の様子をグラフにすると左図のようになります。

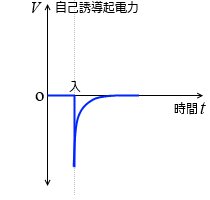発生する自己誘導起電力は左図のようになります。

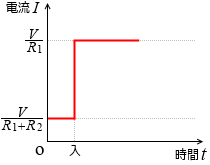もしこの回路にチョークコイルが接続されてなければ、電流の変化は左図のようになります。電流の変化は妨害されてません。曲線は角ばっています。

スイッチを再び開いた瞬間は、電流は小さくなり、コイル内の磁場が弱くなり、そのことによって電磁誘導が起こり、もともと流れている電流と同じ方向に誘導起電力が発生し（自己誘導）、電流の減少を妨害します。時間が経つにつれて（実際には一瞬で）磁場の変化量が小さくなり誘導起電力も小さくなりやがて妨害が止みます。

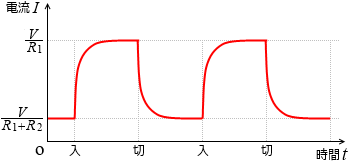チョークコイルが接続されている回路で、スイッチを閉じたり開いたり繰り返した場合の電流の変化は左図のようになります。

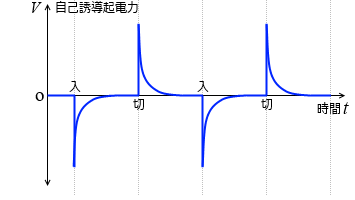そのときの自己誘導起電力は左図のようになります。

上の電流を微分して - を付けたグラフになっています。

自己インダクタンス

自己誘導における誘導起電力の大きさについて考えてみます。

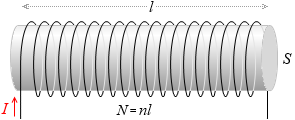長さ l [m] 、断面積 S [m²] 、単位長さ当たりの巻き数 n [回/m] 、巻き数 N (=nl) のコイルがあり、内部に透磁率 μ [N/A²] の鉄心が挿入されているものとし、流れる電流の大きさを I [A] とします。

I [A] の大きさの電流が流れるとき、コイル内部の磁束密度（=ソレノイドがつくる磁束密度 ＊ソレノイドとは導線を密に長く巻いた円筒形のコイルのことです。
　閉じる）B [Wb/m²] は、

　　　　B = μnI

であり、磁束 Φ [Wb] は、これに断面積 S を掛けたものだから、

　　　　Φ = BS = μnIS

であり、発生する誘導起電力 V [V] は、

　　　　V = - N\(\large{\frac{ΔΦ}{Δt}}\)

であり、いま、変化する量は μnIS のうちの I だから、

　　　　V = - N\(\large{\frac{ΔΦ}{Δt}}\) = - N\(\large{\frac{μnSΔI}{Δt}}\)

であり、N = nl だから、

　　　　V = - N\(\large{\frac{μnSΔI}{Δt}}\) = - N\(\large{\frac{μNSΔI}{lΔt}}\) = - \(\large{\frac{μN^2S}{l}}\)⋅\(\large{\frac{ΔI}{Δt}}\)

　　あるいは、

　　　　V = - N\(\large{\frac{μnSΔI}{Δt}}\) = - nl\(\large{\frac{μnSΔI}{Δt}}\) = - μn²lS\(\large{\frac{ΔI}{Δt}}\)

と表せます。

このときの　- \(\large{\frac{μN^2S}{l}}\)⋅\(\large{\frac{ΔI}{Δt}}\)　や　- μn²lS\(\large{\frac{ΔI}{Δt}}\)　の赤字部分を自己インダクタンス＊inductance = induct（誘導する・導入する）+ ance（量・程度を表す名詞語尾）
　閉じるといい、L で表します＊量記号 L はレンツの法則のハインリヒ・レンツ Heinrich Lenz から。
　閉じる。単位は [H] ヘンリー です＊19世紀のアメリカの物理学者 ジョセフ・ヘンリー Joseph Henry から。
斜体の H は磁場の量記号で、エイチと読み、
立体の H は自己インダクタンスの単位で、ヘンリーと読みます。
どちらも語源はジョセフ・ヘンリーです（不確か）。紛らわしいです。
　閉じる。

自己インダクタンスとは

V = - L\(\large{\frac{ΔI}{Δt}}\) という式を見てみますと、自己誘導による誘導起電力 V の大きさは、自己インダクタンス L に比例しています。自己誘導は上で説明したように電流の変化を和らげる作用があります＊「電流」を和らげる、のではありません。
「電流の変化」を和らげる、のです。
　閉じるので、自己インダクタンスが大きい方が電流の変化を和らげる能力が高いということになります。

また、L = μn²lS でありますので、透磁率の大きい物質が挿入されていて、巻きの密度が高くて、長さが長くて、断面積が大きいコイルの方が、その能力が高いといえます。自己インダクタンスはコイルの形状からくる性能を表しているともいえます。

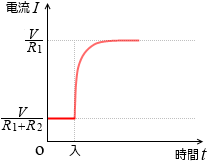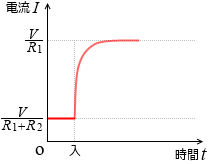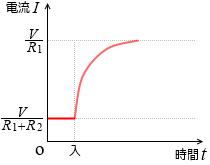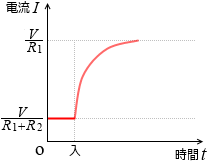自己インダクタンス L が大きいと電流を表すグラフの曲線のカーブはゆるやかになります。L=0 だと直角になります。