円錐振り子

円錐振り子の角速度を求める

長さ l [m] の糸の一端を固定し、他端に質量 m [kg] のおもりを吊るして、このおもりを水平面内で等速円運動させたときの円錐振り子＊糸の運動面が円錐（えんすい）形になるので「円錐振り子」です。

おもりを鉛直面内で振らせれば単振り子です。
　閉じるの運動について考えてみます。

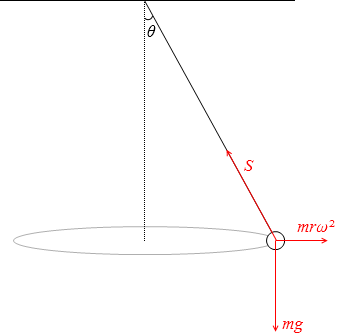
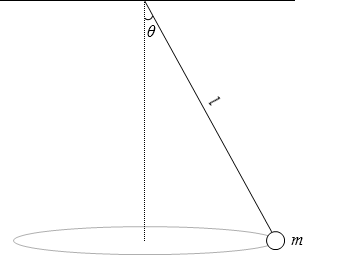鉛直線と糸とのなす角を θ [rad] 、糸の張力を S [N] 、角速度を ω [rad/s] 、重力加速度を g [m/s²] とし、糸は十分軽いものとします。

おもりが等速円運動をしているということは、糸がたるんだり、θ が変化したりすることはないということです。

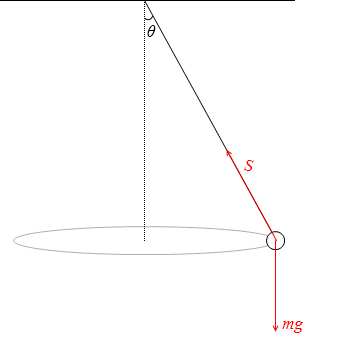おもりにはたらく力は張力 S と重力 mg です。

この２つの力の合力が向心力になっているのですが、鉛直方向と水平方向に別けて考えていきます。

（『遠心力』項の『円錐振り子』もご参照ください）

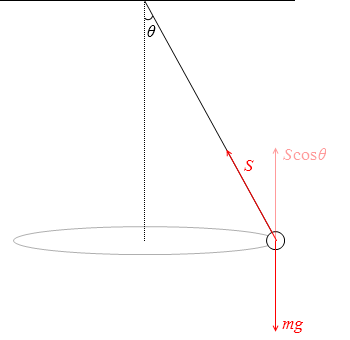鉛直方向について考えますと、
おもりが上にも下にも行かないのは、張力の鉛直成分 Scosθ と重力 mg がつり合っているからです。

　　Scosθ = mg

∴　m = \(\large{\frac{S\cos\theta}{g}}\)　　……①

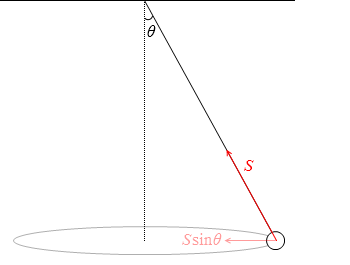水平方向について考えますと、
張力の水平成分 Ssinθ が向心力となって、おもりが等速円運動をしています。

　　Ssinθ = mrω²　　……②

＊ 別の考え方として、

張力 S と反心力（あるいは遠心力）mrω² と重力 mg を合わせると 0 になるから、
　Scosθ = mg
　Ssinθ = mrω²
である、と立式することもできます。
　閉じる

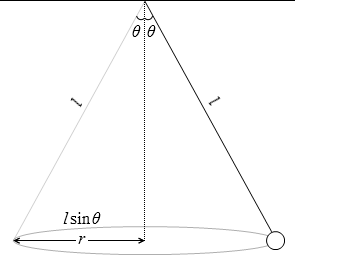等速円運動の円の半径 r は l を用いて表すことができます。

　　r = lsinθ　　……③

②式に、①式と③式を代入します。

　　　　Ssinθ = mrω²

　　　　　　　= \(\large{\frac{S\cos\theta}{g}}\)⋅lsinθ⋅ω²

　∴　　　1 = \(\large{\frac{\cos\theta}{g}}\)⋅l⋅ω²

　∴　　ω² = \(\large{\frac{g}{l\cos\theta}}\)

　∴　　 ω = \(\sqrt{\large{\frac{g}{l\cos\theta}}}\)

周期 T [s] も求めてみますと、

　　　　T = \(\large{\frac{2\pi}{\omega}}\) = \(2\pi\sqrt{\large{\frac{l\cos\theta}{g}}}\)

解釈

上の ω の式を見てみますと、回転スピードは、おもりの質量 m と無関係であることが分かります＊円錐振り子と単振り子では運動の方向が違いますが、『微小振動の単振り子の周期』もご参照ください。
　閉じる。さらに、糸の長さ l が小さいほど、あるいは、角度 θ が大きい（＝cosθ が小さい）ほど、回転スピードが速い、と分かります。

　おもりは　　重くても軽くても回転スピードは変わらない。

　糸の長さは　　短いときの方が回転スピードが速い。

　角度 θ は　　大きいときの方が回転スピードが速い。＊周回半径が大きい上に回転スピードも速いということです。すなわちものすごい周回スピードになっているということです。ものすごいスピードでないと高い位置をキープできないのです。
　閉じる