次の文章を読み、後の問い(問1~問4)に答えよ。
水素原子を、図1のように、静止した正の電気量 \(e\) を持つ陽子と、そのまわりを負の電気量 \(-e\) を持つ電子が速さ \(v\) 、軌道半径 \(r\) で等速円運動するモデルで考える。陽子および電子の大きさは無視できるものとする。陽子の質量を \(M\) 、電子の質量を \(m\) 、クーロンの法則の真空中での比例定数を \(k_0\) 、プランク定数を \(h\) 、万有引力定数を \(G\) 、真空中の光速を \(c\) とし、必要ならば、表1の物理定数を用いよ。
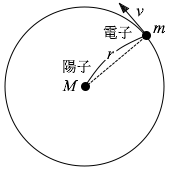 図 1
図 1
表 1 物理定数
| 名称
| 記号
| 数値・単位
|
| 万有引力定数
| \(G\)
| 6.7×10-11 N·m2/kg2
|
| プランク定数
| \(h\)
| 6.6×10-34 J·s
|
| クーロンの法則の真空中での比例定数
| \(k_0\)
| 9.0×109 N·m2/C2
|
| 真空中の光速
| \(c\)
| 3.0×108 m/s
|
| 電気素量
| \(e\)
| 1.6×10-19 C
|
| 陽子の質量
| \(M\)
| 1.7×10-27 kg
|
| 電子の質量
| \(m\)
| 9.1×10-31 kg
|
(問1)qOCC1
(問2)次の文章中の空欄23に入れる数値として最も適当なものを、後の①~⑥のうちから一つ選べ。
水素原子中の電子と陽子の間にはたらくニュートンの万有引力と静電気力の大きさを比較すると、万有引力は静電気力のおよそ 10-23倍であることがわかる。万有引力はこのように小さいので、電子の運動を考える際には、万有引力は無視してよい。
① 10 ② 20 ③ 30 ④ 40 ⑤ 50 ⑥ 60
(問3)次の文章中の空欄24に入れる式として正しいものを、後の①~⑧のうちから一つ選べ。
円運動の向心力は陽子と電子の間にはたらく静電気力のみであるとする。量子数を \(n\)(\(n\)=1,2,3,…)とすると、ボーアの量子条件 \(mvr = n\large\frac{h}{2π}\) は、電子の円軌道の一周の長さが電子のド・ブロイ波の波長の \(n\) 倍に等しいとする定在波(定常波)の条件と一致する。以上の関係から、\(v\) を含まない式で水素原子の電子の軌道半径を表すと、\(r = {\large\frac{h^2}{4π^2k_0me^2}}n^2\) となる。
この結果から、量子条件を満たす電子のエネルギー(運動エネルギーと無限遠を基準とした静電気力による位置エネルギーの和)\(E_n\) を計算すると、\(E_n = -2π^2{k_0}^2\) ×24と求められる。この \(E_n\) を量子数 \(n\) に対応する電子のエネルギー準位という。
① \(\large\frac{me}{nh}\) ② \(\large\frac{m^2e}{n^2h}\) ③ \(\large\frac{me^2}{nh^2}\) ④ \(\large\frac{me^4}{n^2h^2}\)
⑤ \(\large\frac{nh}{me}\) ⑥ \(\large\frac{n^2h}{m^2e}\) ⑦ \(\large\frac{nh^2}{me^2}\) ⑧ \(\large\frac{n^2h^2}{me^4}\)
(問4)次の文中の空欄25に入れる式として正しいものを、後の①~④のうちから一つ選べ。
水素原子中の電子が、量子数 \(n\) のエネルギー準位 \(E\) から量子数 \(n'\) のより低いエネルギー準位 \(E'\) へ移るとき、放出される光子の振動数 \(ν\) は、 \(ν =\)25である。
① \(\large\frac{E'-E}{h}\) ② \(\large\frac{E-E'}{h}\) ③ \(\large\frac{h}{E'-E}\) ④ \(\large\frac{h}{E-E'}\)
#共テ22本試物理
(問2)
電子(質量 \(m\))と陽子(質量 \(M\))の間にはたらくニュートンの万有引力大きさを \(F_{\rm G}\) としますと、
\(F_{\rm G} = G\large\frac{Mm}{r^2}\)
電子(電荷 \(-e\))と陽子(電荷 \(+e\))の間にはたらく静電気力の大きさを \(F_{\rm C}\) としますと、
\(F_{\rm C} = k_0\large\frac{e^2}{r^2}\)
よって、
\(\large\frac{F_{\rm G}}{F_{\rm C}} = \large\frac{G\ Mm}{k_0\ e^2}\)
右辺に表1で示されている各値を代入しますと、
\begin{eqnarray}
\frac{F_{\rm G}}{F_{\rm C}} &=& \frac{6.7×10^{-11}×1.7×10^{-27}×9.1×10^{-31}}{9.0×10^{9}×(1.6×10^{-19})^2} \\[7pt]
&=& \frac{6.7×1.7×9.1×10^{-11}×10^{-27}×10^{-31}}{9.0×1.6×1.6×10^{9}×10^{-19}×10^{-19}} \\[10pt]
&=& \frac{6.7×1.7×9.1×10^{-69}}{9.0×1.6×1.6×10^{-29}} \\[10pt]
&=& \frac{6.7×1.7×9.1}{9.0×1.6×1.6}×10^{-40}
\end{eqnarray}
答えは ④ 40 です。
(問3)
水素原子の電子のエネルギーについては『水素原子のエネルギー準位』で詳しく説明しました。ほぼ同じ説明をここでもいたしますと、
電子のエネルギーというのは電子の運動エネルギーと電子の位置エネルギーの和であるわけですが、
電子の位置エネルギーについては
万有引力 \(F = G{\large\frac{Mm}{r^2}}\) の位置エネルギーが \(U = -G{\large\frac{Mm}{r}}\) なのだから、これと同じように考えて
静電気力 \(F = k_0{\large\frac{e^2}{r^2}}\) の位置エネルギーは
\(U = -k_0{\large\frac{e^2}{r}}\)
電子の運動エネルギーについては
\(K = {\large\frac{1}{2}}mv^2\)
であり、『水素原子のエネルギー準位』項ではこの式に \(mv^2 = k_0{\large\frac{e^2}{r}}\) を代入すると説明したのですが、本問ではボーアの量子条件の式 \(mvr = n\large\frac{h}{2π}\) が与えられているので、これを変形し、
\(v = n\large\frac{h}{2πmr}\)
を上式に代入することにします。そうすると、
\(K = {\large\frac{1}{2}}m × n^2{\large\frac{h^2}{4π^2m^2r^2}} = {\large\frac{h^2}{8π^2mr^2}}n^2\)
よって、電子のエネルギー(量子数 \(n\) を含むので以下「電子のエネルギー準位」)は
\begin{eqnarray}
E_n &=& U + K \\[5pt]
&=& -k_0\frac{e^2}{r} + \frac{h^2}{8π^2mr^2}n^2
\end{eqnarray}
分母の \(r\) の部分に問題文中で与えられた \(r = {\large\frac{h^2}{4π^2k_0me^2}}n^2\) を代入すると、
\begin{eqnarray}
E_n &=& -k_0\frac{e^2}{\frac{h^2}{4π^2k_0me^2}n^2} + \frac{h^2}{8π^2m\frac{h^4}{16π^4{k_0}^2m^2e^4}n^4}n^2 \\[10pt]
&=& -k_0\frac{e^2・4π^2k_0me^2}{h^2n^2} + \frac{h^2・16π^4{k_0}^2m^2e^4}{8π^2m・h^4n^4}n^2 \\[10pt]
&=& -\frac{4π^2{k_0}^2me^4}{h^2n^2} + \frac{2π^2{k_0}^2me^4}{h^2n^2} \\[10pt]
&=& -\frac{2π^2{k_0}^2me^4}{h^2n^2} \\[10pt]
&=& -2π^2{k_0}^2×\textcolor{yellow}{\underline{\textcolor{black}{\frac{me^4}{n^2h^2}}}}
\end{eqnarray}
答えは ④ \(\large\frac{me^4}{n^2h^2}\) です。
(問4)
『仮説2:エネルギー準位の差が光子のエネルギー』で説明したように、電子が量子数 \(n\) のエネルギー準位 \(E\) から量子数 \(n'\) のより低いエネルギー準位 \(E'\) へ移るとき、1個の光子を放出しますが、
光子1個のエネルギーは \(hν\) です。つまり、
\(hν = E - E'\)
です。よって、
\(ν = \textcolor{yellow}{\underline{\textcolor{black}{\large\frac{E-E'}{h}}}}\)
です。
答えは ② \(\large\frac{E-E'}{h}\) です。
