qG87A

図2のように、大きさが R の抵抗、静電容量が C1 、C2 の平行板コンデンサー、起電力が E で内部抵抗が r の電池、スイッチSを接続した回路がある。 はじめ、スイッチSは a の側にあり、コンデンサー C2 には電荷は蓄えられていなかった。

図 2

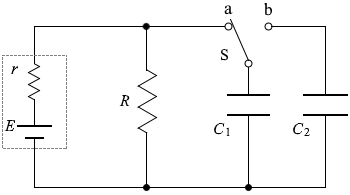
（問3）コンデンサー C1 の両端間の電圧 V1 はいくらか。正しいものを、次の①～④のうちから一つ選べ。

① \(\large{\frac{R+r}{R}}\)E　　② \(\large{\frac{R}{R+r}}\)E

③ \(\large{\frac{R}{R-r}}\)E　　④ \(\large{\frac{R-r}{R}}\)E　　

（問4）次に、スイッチSを b の側にして十分に時間がたったとき、コンデンサー C1 、C2 に蓄えられた電気量は一定となった。 このとき、コンデンサー C2 に蓄えられた電気量を C1 、C2 、V1 で表すとどのようになるか。正しいものを、次の①～⑥のうちから一つ選べ。

① C1V1　　　　② C2V1　　　　③ (C1 + C2)V1

④ \(\large{\frac{{C_1}^2}{C_1+C_2}}\)V1　　⑤ \(\large{\frac{C_1C_2}{C_1+C_2}}\)V1　　⑥ \(\large{\frac{{C_2}^2}{C_1+C_2}}\)V1

（問5）次に、スイッチSを b の側にしたまま、コンデンサー C2 の電極間を比誘電率が 1 より大きい誘電体で満たした。このとき、コンデンサー C2 に蓄えられる電気量はどのようになるか。最も適当なものを、次の①～⑤のうちから一つ選べ。

① コンデンサー C2 の電気容量が大きくなるので、蓄えられる電気量は増加する。
② コンデンサー C2 の電気容量が大きくなるので、蓄えられる電気量は減少する。
③ コンデンサー C2 の電気容量が小さくなるので、蓄えられる電気量は増加する。
④ コンデンサー C2 の電気容量が小さくなるので、蓄えられる電気量は減少する。
⑤ 電気量は保存されるので変化しない。

#センター04追試

（問3）
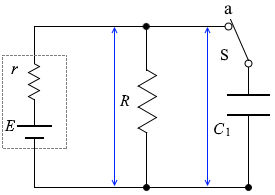コンデンサー C1 に掛かる電圧と抵抗 R に掛かる電圧は同じであり、

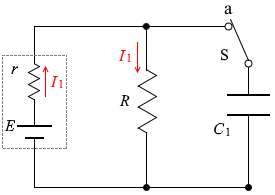内部抵抗 r に流れる電流を I1 とすると、（充電が完了しているコンデンサーには電流は流れないので）抵抗 R に流れる電流も I1 であり、抵抗 R に掛かる電圧は RI1 となります。

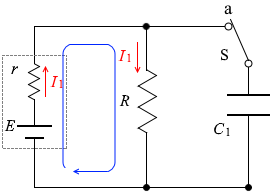左図のような経路についてのキルヒホッフ第2法則の式を立てますと、

　　rI1 + RI1 = E

∴　I1 = \(\large{\frac{E}{r+R}}\)

と I1 が求まりますので、

抵抗 R に掛かる電圧は

　　　　RI1 = R\(\large{\frac{E}{r+R}}\) = \(\large{\frac{R}{R+r}}\)E

であり、これがコンデンサー C1 の両端間の電圧 V1 です。答えは ② です。

（問4）次に、スイッチSを b の側にして十分に時間がたったとき、コンデンサー C1 、C2 に蓄えられた電気量は一定となった。 このとき、コンデンサー C2 に蓄えられた電気量を C1 、C2 、V1 で表すとどのようになるか。正しいものを、次の①～⑥のうちから一つ選べ。

① C1V1　　　　② C2V1　　　　③ (C1 + C2)V1

④ \(\large{\frac{{C_1}^2}{C_1+C_2}}\)V1　　⑤ \(\large{\frac{C_1C_2}{C_1+C_2}}\)V1　　⑥ \(\large{\frac{{C_2}^2}{C_1+C_2}}\)V1

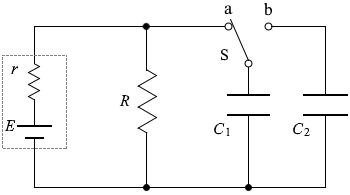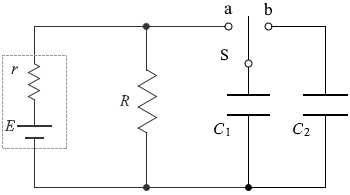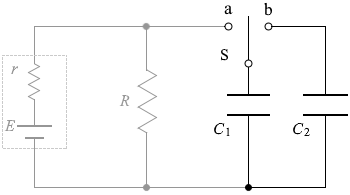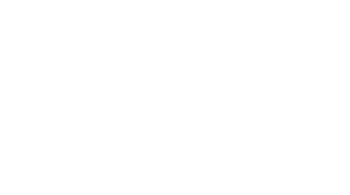スイッチSを a から離すということは、電池 E や抵抗 R と断絶して無関係になるということです。

そして、スイッチSを b の側に入れるということは、コンデンサー C1 に溜まっていた電荷がコンデンサー C2 に移動するということです（『コンデンサーの並列接続』参照）。

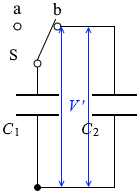移動が終わると C1 の電圧と C2 の電圧が等しくなります（『コンデンサーの並列接続』参照）。この電圧を V' と置きます。

スイッチSを b 側に入れる前の電気量を Q0 としますと、

　　　　Q0 = C1V1　　……➊

であり、b 側に入れた後の、コンデンサー C1 の電気量を Q1 、コンデンサー C2 の電気量を Q2 としますと、

　　　　Q1 = C1V'　　Q2 = C2V'　　……➋

です。そして、電気量保存の法則より、

　　　　Q0 = Q1 + Q2

であるはずだから、これに➊式と➋式を代入すると、

　　　　C1V1 = C1V' + C2V'

となり、

　∴　　C1V1 = (C1 + C2)V'

　∴　　V' = \(\large{\frac{C_1}{C_1+C_2}}\)V1

と V' が求められまして、これを再び➋式に入れ戻しますと、

　　　　Q1 = \(\large{\frac{{C_1}^2}{C_1+C_2}}\)V1　　Q2 = \(\large{\frac{C_1C_2}{C_1+C_2}}\)V1

と求められます。答えは ⑤ です。

（問5）次に、スイッチSを b の側にしたまま、コンデンサー C2 の電極間を比誘電率が 1 より大きい誘電体で満たした。このとき、コンデンサー C2 に蓄えられる電気量はどのようになるか。最も適当なものを、次の①～⑤のうちから一つ選べ。

① コンデンサー C2 の電気容量が大きくなるので、蓄えられる電気量は増加する。
② コンデンサー C2 の電気容量が大きくなるので、蓄えられる電気量は減少する。
③ コンデンサー C2 の電気容量が小さくなるので、蓄えられる電気量は増加する。
④ コンデンサー C2 の電気容量が小さくなるので、蓄えられる電気量は減少する。
⑤ 電気量は保存されるので変化しない。

電極間を誘電体で満たすと電気容量は大きくなります。もし、電気量がそのままだとすると電圧は下がります（Q = CV の Q 一定のまま C が大きくなると V が小さくなる）。しかし、コンデンサー C1 とコンデンサー C2 は並列につながっているので電圧は等しく保たれようとします。電荷が移動するということです（上の問4で例示した、電荷が5個の内3個が移動するアニメーションにおいて、さらにもう1個移動して、電圧を等しく保とうとします）。つまり、コンデンサー C2 電気量は増加します。

というわけで答えは ① です。

　

（ちなみに、電気容量の別名が静電容量です。2つは同一のものです。）

↑ ↓