qI7H2

この問題のポイントは力の掛かり具合がどうなっているかということです。

左側の手が F という大きさの力で引っ張っている場合、

真ん中の部分は同じく F の大きさの力で引っ張り返し、

F の大きさの力で引っ張り返され、

そして右側の手は F の大きさの力で引っ張っています。

どこもかしこも同じ大きさの力で引っ張っています。張力と同じです。

もし、違う大きさの力で引っ張っているとしたら、ばねは動き出してしまいます。ばねが静止している（問題文には静止とは書いてないですが題意より静止していることは明らかです）のは力がつり合っているからであり、力の大きさが同じということです。

それから、

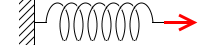これと

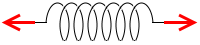これは、力の掛かり方がまったく同じです。片方の力の大きさが F であれば、両側から F の力で引っ張っても、ばねに掛かる力の大きさは F です。2F などということはありません。

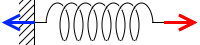壁には F の力が隠れています。作用⋅反作用の法則です。

（『qHBF8』参照）

というわけで、k のばねにも 2k のばねにも同じ力が掛かっていて、この力の大きさを F と置いてそれぞれのばねに関するフックの法則の式を立てますと、

　k のばね ： F = k × x

　2k のばね ： F = 2k × y

　∴　　kx = 2ky

　∴　　 \(\large{\frac{x}{y}}\) = 2

となります。

本問は物理の基本を理解しているかを問うとても良い問題です。