図5のように、動滑車と定滑車を組み合わせて質量 m の荷物をつり上げる。伸び縮みしないひもの一端を天井に固定し、他端を一定の力 F で引いたところ、荷物は上昇した。このとき、荷物の加速度の大きさ a はいくらか。ただし、滑車およびひもの質量は無視でき、滑車はなめらかに回転するものとする。また、重力加速度の大きさを g とする。
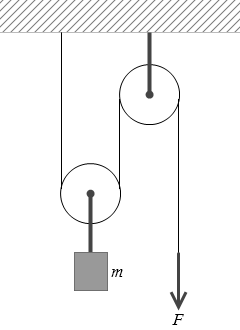
#センター08追試
図5のように、動滑車と定滑車を組み合わせて質量 m の荷物をつり上げる。伸び縮みしないひもの一端を天井に固定し、他端を一定の力 F で引いたところ、荷物は上昇した。このとき、荷物の加速度の大きさ a はいくらか。ただし、滑車およびひもの質量は無視でき、滑車はなめらかに回転するものとする。また、重力加速度の大きさを g とする。

#センター08追試
加速度を聞かれているので運動方程式を立てます。
運動方程式を立てるために、荷物に関わる力をすべて書き出してみます。
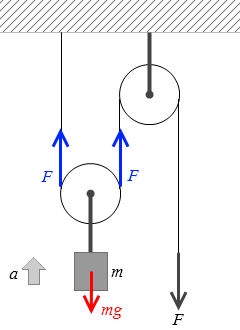 張力の大きさは F です。『滑車につるされた2物体』の場合とは違います。本問はひもの片端が固定されてますので、作用反作用の法則により、ただちに張力の大きさが F 、と確定します。
張力の大きさは F です。『滑車につるされた2物体』の場合とは違います。本問はひもの片端が固定されてますので、作用反作用の法則により、ただちに張力の大きさが F 、と確定します。
荷物に関する運動方程式を立てますと、
ma = 2F - mg
∴ a = \(\large{\frac{2F}{m}}\) - g
(余談1:滑車における張力というものの考え方)
ひものあらゆる部分に同じ大きさの張力がはたらいていることに気をつけてください。
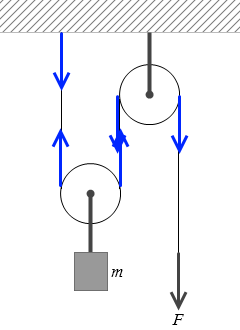 張力をすべて書き出してみますと左図のようになります。
張力をすべて書き出してみますと左図のようになります。
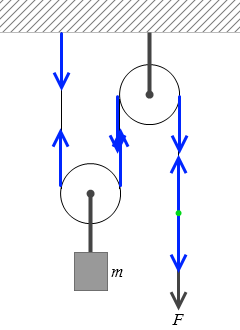 さらにいえば、ひもの途中の箇所(左図の緑点)にも張力ははたらいているといえます。ひもを構成する分子を引きちぎろうとしています。
さらにいえば、ひもの途中の箇所(左図の緑点)にも張力ははたらいているといえます。ひもを構成する分子を引きちぎろうとしています。
これらの力の中で、荷物に関わりのある力だけを書き出して問題を解きます。
もし問題が、「2つの滑車のうち、定滑車にはたらく力を図示せよ」というものだったら、以下のようになります。
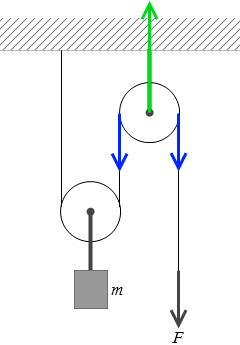 上向きの 2F の力と、下向きの F の力2つがつり合って定滑車は静止しています。
上向きの 2F の力と、下向きの F の力2つがつり合って定滑車は静止しています。
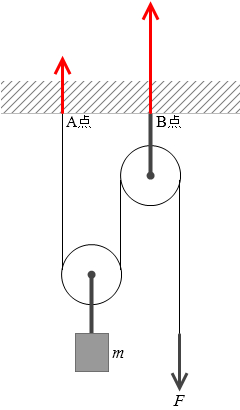 さらに、このことから分かるのは左図のA点、B点では、B点の方が倍の力が掛かっているということです。
さらに、このことから分かるのは左図のA点、B点では、B点の方が倍の力が掛かっているということです。
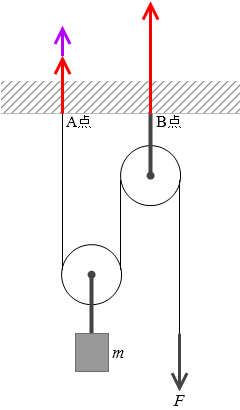 このとき、mg の重さが余計に掛かるのでは、などと考えるのは間違いです。
このとき、mg の重さが余計に掛かるのでは、などと考えるのは間違いです。
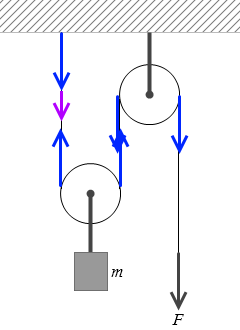 そのように考えてしまったら、A点を引っ張る張力も大きいということになってしまいます。各張力のうち一つだけ大きいということになってしまいます。
そのように考えてしまったら、A点を引っ張る張力も大きいということになってしまいます。各張力のうち一つだけ大きいということになってしまいます。
張力というのは一本でつながっているひもにおいてはどこもかしこも必ず同じ大きさになっています。…となれば、すべての箇所の張力が大きくなる、ということになってしまいます。
 そうではなくて、はじめの F という張力の中に mg の重さが含まれているのです。
そうではなくて、はじめの F という張力の中に mg の重さが含まれているのです。
この F という大きさの力が、ひものあらゆる箇所に行き渡っています。
(余談2:荷物が静止しているとき)
荷物が上昇も下降もしておらず静止しているとき、
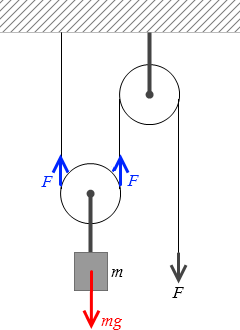 2F と mg がつり合っているから、
2F と mg がつり合っているから、
F = \(\large{\frac{mg}{2}}\)
となります。
(余談3:仕事)
F の力で引いているのに荷物には 2F の力がはたらいていることに違和感があるかもしれませんが、これはそういうものです。動滑車とは、倍の力で物を持ち上げるときに使う道具です。テコの原理と同じです。力が2倍になりましたが、移動距離は \(\large{\frac{1}{2}}\) です。トータルでつじつまが合います。
本問は仕事について聞かれているのではなく加速度を聞かれているので、移動距離は問題になりません。
(余談4:シーソー)
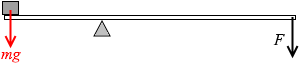 水平なシーソーにおいて距離が2倍離れた位置に下向きの F の大きさの力を加えた場合の荷物の加速度も
水平なシーソーにおいて距離が2倍離れた位置に下向きの F の大きさの力を加えた場合の荷物の加速度も
a = \(\large{\frac{2F}{m}}\) - g
となります。
ma = 2F - mg
という運動方程式が立てられるからです。
このシーソーの問題と本問は本質的なものは全く同じです。