(張力はどこでも一緒)
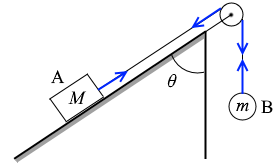 ピンと張った糸においては、どの地点においても張力は同じです。この場合物体Bの重力が張力になっています。mg です。
ピンと張った糸においては、どの地点においても張力は同じです。この場合物体Bの重力が張力になっています。mg です。
(綱引き)
この問題は物体Aと物体Bが綱引きをしていると見立てることができます。
 θ が小さいときは物体Aが勝ちそうですし、θ が大きいときは物体Bが勝ちそうです。
θ が小さいときは物体Aが勝ちそうですし、θ が大きいときは物体Bが勝ちそうです。
(運動方向とそれに垂直な方向に分解)
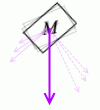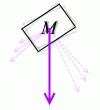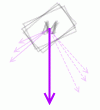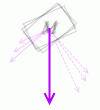 斜面上の物体の重力は、(運動方向)と(それに垂直な方向)に分解して考えます。
斜面上の物体の重力は、(運動方向)と(それに垂直な方向)に分解して考えます。
(θ の設定)
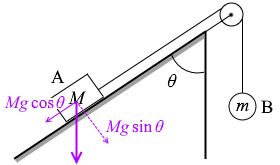 今は頂角を θ と置いていて、物体Aの重力の運動方向の大きさが Mgcosθ で、それに垂直な方向の大きさが Mgsinθ となっていますが、
今は頂角を θ と置いていて、物体Aの重力の運動方向の大きさが Mgcosθ で、それに垂直な方向の大きさが Mgsinθ となっていますが、
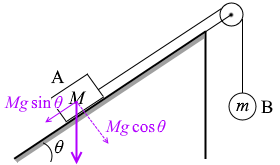 仰角が θ とされている場合は sin と cos が逆転します。間違いやすいです。
仰角が θ とされている場合は sin と cos が逆転します。間違いやすいです。
(摩擦力の向きは運動しようとする向きと逆)
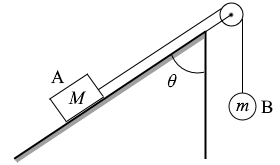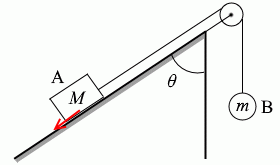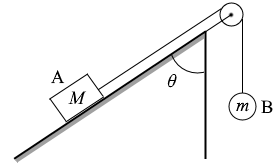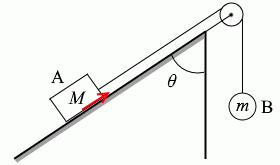 摩擦力というのは動きを邪魔する方向にはたらく力です。常に逆向きにはたらきます。物体Aが上に行こうとするときは下向きに、物体Aが下に行こうとするときは上向きにはたらきます。
斜面の角度によっては物体Aと物体Bの引っ張り合いがつり合って、
摩擦力というのは動きを邪魔する方向にはたらく力です。常に逆向きにはたらきます。物体Aが上に行こうとするときは下向きに、物体Aが下に行こうとするときは上向きにはたらきます。
斜面の角度によっては物体Aと物体Bの引っ張り合いがつり合って、
摩擦力がちょうど 0 になるということも起こりえます。
『静止摩擦力』の「外力と静止摩擦力は大きさが同じです。常に同じです*」
の「*」中の説明もご覧ください。
(力をすべて書き出す)
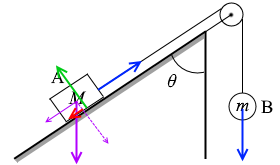 力をすべて書き出すと左図のようになります。
力をすべて書き出すと左図のようになります。
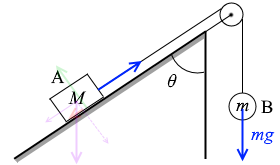 張力は mg です。
張力は mg です。
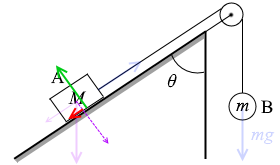 垂直抗力の大きさは Mgsinθ と同じです。問題文より静止摩擦係数が μ であるので、摩擦力の大きさは、摩擦係数と垂直抗力を掛けて μMgsinθ です。今は、右上に動き出すのを食い止めているので摩擦力の向きは左下です。
垂直抗力の大きさは Mgsinθ と同じです。問題文より静止摩擦係数が μ であるので、摩擦力の大きさは、摩擦係数と垂直抗力を掛けて μMgsinθ です。今は、右上に動き出すのを食い止めているので摩擦力の向きは左下です。
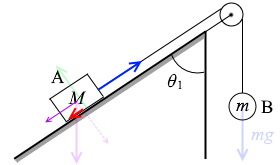 物体Aが上向きにすべり出す直前に、動き出さずに静止しているというのは、張力 mg と物体Aの重力の運動方向成分 Mgcosθ1 と摩擦力 μMgsinθ1 の3つの力がつり合っているからです。
物体Aが上向きにすべり出す直前に、動き出さずに静止しているというのは、張力 mg と物体Aの重力の運動方向成分 Mgcosθ1 と摩擦力 μMgsinθ1 の3つの力がつり合っているからです。
つり合いの式を立てて解きますと、
mg = Mgcosθ1 + μMgsinθ1
∴ m = Mcosθ1 + μMsinθ1
∴ \(\large{\frac{m}{M}}\) = cosθ1 + μsinθ1
となります。
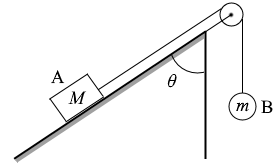
 ピンと張った糸においては、どの地点においても
ピンと張った糸においては、どの地点においても θ が小さいときは物体Aが勝ちそうですし、θ が大きいときは物体Bが勝ちそうです。
θ が小さいときは物体Aが勝ちそうですし、θ が大きいときは物体Bが勝ちそうです。
 今は頂角を θ と置いていて、物体Aの重力の運動方向の大きさが
今は頂角を θ と置いていて、物体Aの重力の運動方向の大きさが  仰角が θ とされている場合は
仰角が θ とされている場合は 
 力をすべて書き出すと左図のようになります。
力をすべて書き出すと左図のようになります。 張力は
張力は 
 物体Aが上向きにすべり出す直前に、動き出さずに静止しているというのは、張力
物体Aが上向きにすべり出す直前に、動き出さずに静止しているというのは、張力