図7のように、あらい斜面の上に質量 M の物体Aを置く。Aには糸で質量 m のおもりBがつながれ、Bは滑車を通して鉛直につり下げられている。斜面が鉛直方向となす角度（頂角）θ は 0° < θ ≦ 90° の範囲で変えることができる。Aと滑車の間では糸は常に斜面に平行に保たれる。Aと斜面の間の静止摩擦係数を μ 、動摩擦係数を μ' 、重力加速度の大きさを g とする。
（問7）qG6Q8
（問8）図8のように斜面を水平（θ = 90°）にし、Aを面上に置いて静かに離したところ、Bは降下し始めた。Bが距離 h だけ降下したときのAの速さはいくらか。ただし、このときAは面の端まで達していないとする。
#センター10本試
（まず加速度を求める）
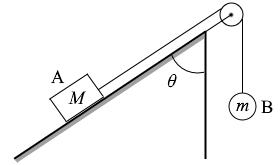
物体Aと物体Bは糸でつながれていて糸はピンと張っているので、物体Aの加速度と物体Bの加速度は同じです。もし物体Bの加速度の方が大きかったりしたらそれは物体Aと物体Bの距離が変化するということで、それはつまり糸が切れるということになってしまいます。逆に、物体Bの加速度の方が小さかったとしたらそれは糸がたるんでしまっているということです。物体Aは引っ張られていないということです。動かないということです。これはおかしいです。
というわけで、物体Aと物体Bの加速度は同じです（速さも同じ）。これを a と置きます。
（張力）
ピンと張った糸においては、どの地点においても張力は同じであるのは qG6Q8 と一緒なのですが、その大きさは mg ではありません。静止してないので物体Bの重力と張力がつり合っているわけではありません。どのくらいの大きさなのかは分かりません。
この張力を T と置きます。
（運動方程式を立てる）
運動方程式（エムエーイコールエフの式）を立てて a を求めます。
まず物体Aについては、
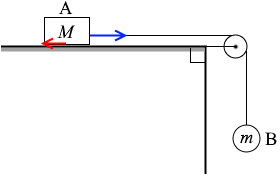張力 T と摩擦力がはたらいています。
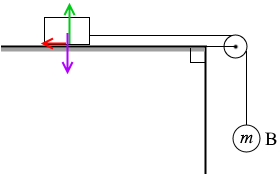摩擦力の大きさは（摩擦係数）×（垂直抗力）であり、（垂直抗力）の大きさは床に押し付ける力と同じ大きさであり、それは Mg です。よって摩擦力は μ'Mg です。
すなわち物体Aの運動方程式は
Ma = T - μ'Mg ……①
です。
一方、物体Bについては、
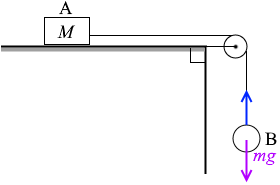張力 T と重力 mg がはたらいています。
すなわち物体Bの運動方程式は
ma = mg - T ……②
です。
①式、②式の辺々を加えますと、
Ma + ma = T - μ'Mg + mg - T
∴ (M + m)a = mg - μ'Mg ……③
∴ (m + M)a = (m - μ'M)g
∴ a = \(\large{\frac{m-μ'M}{m+M}}\)g
（慣れてる人は、③式をいきなり立てても構いません。物体Aと物体Bを一体とみなして、そこにはたらく力は重力 mg と摩擦力 μ'Mg だ、と考えるのです。張力は考えません。）
（等加速度直線運動の式に代入）
加速度が求められたので、等加速度直線運動の時間を含まない式（v2 - v02 = 2ax）を立式して速さを求めます。
v2 - 02 = 2ah
v2 = 2×\(\large{\frac{m-μ'M}{m+M}}\)g×h
∴ v = \(\sqrt{\large{\frac{2gh(m-μ'M)}{m+M}}}\)
（別解：エネルギー保存の法則から考える）
もっと慣れた人はエネルギー保存の法則から導き出してしまいます。
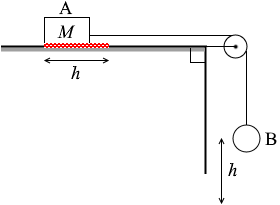始めにあった位置エネルギー mgh
mgh というのは物体Bが持っていた位置エネルギーです。
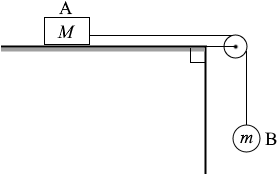
物体Aについては位置エネルギーに変化はありません。高さが変わらないので。
が、
運動エネルギー \(\large{\frac{1}{2}}\)(m+M)v2 と
摩擦熱 μ'Mgh
摩擦力がした仕事は（摩擦力μ'Mg）×（距離h）で、
つまり μ'Mgh であり、これが摩擦熱です。
に変わった、
と考えるのです。
すなわち、
mgh = \(\large{\frac{1}{2}}\)(m+M)v2 + μ'Mgh
∴ \(\large{\frac{1}{2}}\)(m+M)v2 = mgh - μ'Mgh
∴ (m+M)v2 = 2gh(m - μ'M)
∴ v = \(\sqrt{\large{\frac{2gh(m-μ'M)}{m+M}}}\)
となり、あっという間に答が得られます。