あらい水平面上での質量 m の物体の運動を考える。図3のように、一端を固定したばねを自然の長さから d だけ縮め、他端に物体を置いて手で押さえた。次に、手を離すと物体は初速度 0 で動き始め、やがてばねから離れて、手を離したときの位置から x だけ進んで止まった。x はいくらか。ただし、ばねの質量は無視できるものとする。また、ばね定数を k 、面と物体の間の動摩擦係数を μ' 、重力加速度の大きさを g とする。
#センター09追試
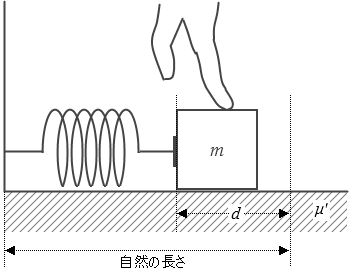
あらい水平面上での質量 m の物体の運動を考える。図3のように、一端を固定したばねを自然の長さから d だけ縮め、他端に物体を置いて手で押さえた。次に、手を離すと物体は初速度 0 で動き始め、やがてばねから離れて、手を離したときの位置から x だけ進んで止まった。x はいくらか。ただし、ばねの質量は無視できるものとする。また、ばね定数を k 、面と物体の間の動摩擦係数を μ' 、重力加速度の大きさを g とする。

#センター09追試

この問題は qGAC1 のような等加速度直線運動の問題ではありません。あちらの問題はすべり始めてから停止するまでの間、はたらく力は摩擦力だけでしたので、「等加速度」でしたが、こちらは途中までばねの力も加わるので「等加速度」ではありません。
ではどうするかというと、エネルギー(=仕事)に着目して解きます。qGAC1 の(別解)、『あらい水平面を進む物体』、『ΔE = W の式』のようにエネルギー保存の法則の式を立てます。
d だけ縮めたときの弾性エネルギーは \(\large{\frac{1}{2}}\)kd2 で、運動エネルギーは 0 で、
物体が止まったときは、弾性エネルギーが 0 で、運動エネルギーも 0 です。
この間、動摩擦力がした仕事は( - Fs =)- μ'mg × x です。
よって、
(0 + 0) - (\(\large{\frac{1}{2}}\)kd2 + 0) = - μ'mg × x
\(\large{\frac{1}{2}}\)kd2 = μ'mgx
慣れていれば、弾性エネルギーが摩擦熱に変わったと考えて、いきなり、
\(\large{\frac{1}{2}}\)kd2 = μ'mgx
と立式して構いません。
∴ x = \(\large{\frac{k}{2μ'mg}}\)d2
k が大きい(ばねが強い)、あるいは d が大きい(うんと縮める)、あるいは μ' が小さい(摩擦が小さい)、あるいは m が小さい(物体が軽い)と距離 x が伸びます。(この x は自然長からの距離ではないのでご注意)
(余談:自然長の位置を通過するときの物体の速さ)
自然長の位置を通過するときの物体の速さを v1 と置きます。
d だけ縮めた位置での弾性エネルギーは
\(\large{\frac{1}{2}}\)kd2
自然長の位置までに発生する摩擦熱は
μ'mgd
自然長の位置での運動エネルギーは
\(\large{\frac{1}{2}}\)mv12
エネルギー保存則より、
\(\large{\frac{1}{2}}\)kd2 = μ'mgd + \(\large{\frac{1}{2}}\)mv12
∴ kd2 = 2μ'mgd + mv12
∴ mv12 = kd2 - 2μ'mgd
∴ v12 = \(\large{\frac{k}{m}}\)d2 - 2μ'gd
これのルートが v1 です。
(余談:時間を含まない式を立てて検算してみる)
自然長の位置から止まる位置までは等加速度運動であり、このときの加速度を a と置き、qGAC1 を参考にしてこれを求めると、
動摩擦力の大きさが
- μ'mg
で、運動方程式を立てると、
ma = - μ'mg
よって加速度は
a = - μ'g
等加速度直線運動の時間を含まない式(v2 - v02 = 2ax)を立てますと、
02 - v12 = 2a(x - d)
∴ 02 - v12 = - 2μ'g(x - d)
∴ v12 = 2μ'g(x - d)
∴ \(\large{\frac{k}{m}}\)d2 - 2μ'gd = 2μ'g(x - d)
∴ \(\large{\frac{k}{2μ'mg}}\)d2 - d = (x - d)
∴ x = \(\large{\frac{k}{2μ'mg}}\)d2
上で求めた答えと一致します。
(余談:ちょうど自然長の位置で止めるには)
上式の x に d を代入して、
d = \(\large{\frac{k}{2μ'mg}}\)d2
∴ 1 = \(\large{\frac{k}{2μ'mg}}\)d
∴ d = \(\large{\frac{2μ'mg}{k}}\) ……①
このような条件が成り立つときに、ちょうど自然長の位置で物体が止まります。
(余談:自然長に達しない位置で止まるのか)
問題文に
「手を離すと物体は動き始め、」とあるので、物体が全く動かないことはない、
「やがてばねから離れて、」とあるので、自然長の位置より遠くに進む、
ということが前提になってますが、
最大静止摩擦力がとても大きかったりすれば、物体が全く動かないこともありえますし、
①式を満たさず d < \(\large{\frac{2μ'mg}{k}}\) だったりすれば、自然長の位置に達する前に止まってしまうこともありえます。このときは、止まった上で、あらためて最大静止摩擦力がどれくらい強いかによって動き出すか止まったままであるかが決まります。