図3のように、振動数 f の単色光が、空気中から一様な厚さ d の薄膜に垂直に入射している。境界面Aで反射した光と、境界面Bで反射した光は、空気中で干渉する。空気の絶対屈折率を 1 、薄膜の絶対屈折率を n とする。光の位相は、境界面Aで反射するときには π だけ変化するが、境界面Bで反射するときには変化しない。
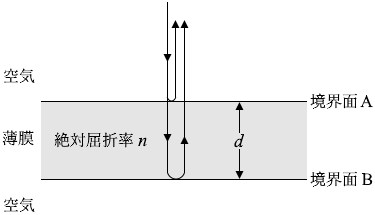
（問3）次の文章中の空欄ウ・エに入れる式の組合せとして正しいものを、下の①～⑧のうちから一つ選べ。
境界面Aから薄膜に入り境界面Bで反射した光は、再び境界面Aに到達する。この光が薄膜内を往復するのに要する時間 t は、真空中における光の速さを c として、ウと表される。また、境界面Aと境界面Bで反射した二つの光が強めあう条件は、m を正の整数として、t =エと表される。
| ウ | エ | |
|---|---|---|
| ① | \(\large{\frac{2d}{nc}}\) | \(\large{\frac{m}{f}}\) |
| ② | \(\large{\frac{2d}{nc}}\) | \(\big(m-\large{\frac{1}{2}}\)\(\big)\large{\frac{1}{f}}\) |
| ③ | \(\large{\frac{2d}{nc}}\) | \(\large{\frac{mn}{f}}\) |
| ④ | \(\large{\frac{2d}{nc}}\) | \(\big(m-\large{\frac{1}{2}}\)\(\big)\large{\frac{n}{f}}\) |
| ⑤ | \(\large{\frac{2nd}{c}}\) | \(\large{\frac{m}{f}}\) |
| ⑥ | \(\large{\frac{2nd}{c}}\) | \(\big(m-\large{\frac{1}{2}}\)\(\big)\large{\frac{1}{f}}\) |
| ⑦ | \(\large{\frac{2nd}{c}}\) | \(\large{\frac{mn}{f}}\) |
| ⑧ | \(\large{\frac{2nd}{c}}\) | \(\big(m-\large{\frac{1}{2}}\)\(\big)\large{\frac{n}{f}}\) |
（問4）次の文章中の空欄オ〜キに入れる語の組合せとして最も適当なものを、下の①～⑥のうちから一つ選べ。
厚さを調節できる薄膜に対して垂直に単色光を入射させた。薄膜が光の波長より十分に薄いとき、単色光の色によらず二つの反射光はオあった。その状態から薄膜を徐々に厚くしていくと、二つの反射光は一度カあった後、厚さ d1 のとき再びオあった。単色光が赤色、緑色、青色の場合で比較すると、d1 が最も小さいのはキ色の場合であった。
| オ | カ | キ | |
|---|---|---|---|
| ① | 弱め | 強め | 赤 |
| ② | 弱め | 強め | 緑 |
| ③ | 弱め | 強め | 青 |
| ④ | 強め | 弱め | 赤 |
| ⑤ | 強め | 弱め | 緑 |
| ⑥ | 強め | 弱め | 青 |
#センター16本試物理
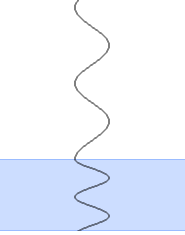このような状態ではなく、
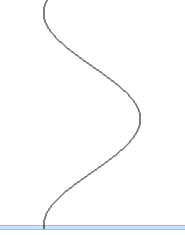このような状態ということです。
境界面A（上面）で
境界面B（下面）で反射した光の位相は変化しないので（線対称）、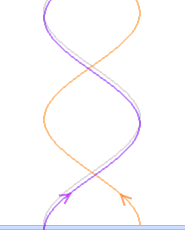
二つの反射光は位相が π だけズレていることになり、
そしてこの状態から薄膜を徐々に厚くしていくと、やがて位相がそろい、二つの反射光は 強め あいます。
さらに厚くしていくと、位相が π ズレて、二つの反射光は再び弱めあいます。
このときの厚さ d1 は半波長分