物質波
物質波とは
『光電効果と光量子仮説』項、『コンプトン効果』項で波動であるはずの光に粒子性があることを説明しましたが、ド・ブロイ 1892年–1987年のフランスの物理学者、ルイ・ド・ブロイ。 はこれとは逆に粒子に波動性があるのではないかと考えました。
光子の運動量は \(p\) = \(\large{\frac{h}{λ}}\) でありますが、あらゆる粒子においてもこの式は成り立つと考えました。
上式を変形すると \(λ\) = \(\large{\frac{h}{p}}\) であり、\(p\) = \(mv\) を代入すると \(λ\) = \(\large{\frac{h}{p}}\) = \(\large{\frac{h}{mv}}\) であり、このときの波を物質波あるいはド・ブロイ波といいます。特に電子の場合、電子波といいます。
物質波（ド・ブロイ波）
\(λ\) = \(\boldsymbol{\large{\frac{h}{p}}}\) = \(\boldsymbol{\large{\frac{h}{mv}}}\)
この波は電子以外にも陽子や中性子にもみられます。理論的には運動する物体すべてにみられます 飛んでいるボールにも存在しますが小さすぎて検出できません。 。突拍子もない考えのようではありますが、この理論が量子力学へとつながっていきました。
たとえば、
速さ 30m/s で飛んでいる質量 220g のボールの物質波の波長は
\(λ\) = \(\large{\frac{h}{mv}}\) = \(\large{\frac{6.6×10^{-34}}{0.22×30}}\) = \(\large{\frac{6.6×10^{-34}}{6.6}}\) = 1.0×10-34 [m]
速さ 1.1×106m/s で飛んでいる電子の物質波（電子波）の波長は
\(λ\) = \(\large{\frac{h}{mv}}\) = \(\large{\frac{6.6×10^{-34}}{9.1×10^{-31}×1.1×10^{6}}}\) ≒ \(\large{\frac{6.6×10^{-34}}{10×10^{-25}}}\) = 6.6×10-10 [m]
です。
電子波の波長
物質波の中で電子波について、その波長を求めてみます。
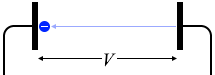たとえばボールを加速させるには手で持って投げればいいですが、電子は手でつかむことができないので、電圧を掛けて加速させます。
陰極に静止していた電子を \(V\) [V] の電位差で加速させ、陽極に到達したときのその直前の電子波の波長について考えてみます。電子の電気量を -\(e\) [C]、質量を \(m\) [kg]、陽極に到達する直前の速さを \(v\) [m/s]、運動量を \(p\) [kg⋅m/s]、波長を \(λ\) [m] とします。（つまりこれは電子線のことです。陰極線のことです。）
スタート地点の陰極での電子の位置エネルギーは \(eV\) [J] で -\(e\) [C] の電荷を -\(V\) [V] の電位差間を運ぶエネルギーは \(eV\) [J] 、スタート後徐々に位置エネルギーが減っていって速度が大きくなっていき、つまり運動エネルギーが大きくなっていき、ゴール地点の陽極では位置エネルギーが 0 になり運動エネルギーが \({\large\frac{1}{2}}mv^2\) [J] になります。力学的エネルギー保存の法則です。（『\(\large{\frac{1}{2}}\)\(mv\)2 = \(mgh\) のような話』参照 あちらの話とちょっと違うのは、あちらは地面から球を打ち上げるかのような話で、こちらは木の枝のリンゴを切って落とすかのような話です。でもどちらも力学的エネルギー保存の法則の話です。 ）
\({\large\frac{1}{2}}mv^2\) = \(eV\)
∴ \(mv\)2 = 2\(eV\)
↓↳ ∴ \(v\) = \(\sqrt{\frac{2eV}{m}}\)
∴ (\(mv\))2 = 2\(meV\)
∴ \(mv\) = \(\sqrt{2meV}\)
∴ \(p\) = \(mv\) = \(\sqrt{2meV}\)
これを物質波（ド・ブロイ波）の式に代入しますと、
\(λ\) = \(\large{\frac{h}{p}}\) = \(\large{\frac{h}{mv}}\) = \(\large{\frac{h}{\sqrt{2meV}}}\)
これらの式に具体的に、プランク定数 \(h\) = 6.63×10-34 [J⋅s]、電気素量 \(e\) = 1.60×10-19 [C]、電子の質量 \(m\) = 9.11×10-31 [kg] を代入してみますと、
\(v\) = \(\sqrt{\frac{2eV}{m}}\) = \(\sqrt{\frac{2×1.60×10^{-19}×V}{9.11×10^{-31}}}\)
\(p\) = \(mv\) = \(\sqrt{2meV}\)
\(λ\) = \(\large{\frac{h}{\sqrt{2meV}}}\) = \(\large{\frac{6.63×10^{-34}}{\sqrt{2×9.11×10^{-31}×1.60×10^{-19}×V}}}\) = \(\large{\frac{\sqrt{6.63^{2}}×10^{-34}}{\sqrt{2×9.11×1.60×V}×10^{-25}}}\) = \(\sqrt{\frac{6.63^{2}}{2×9.11×1.60×V}}\)×10-9 ≒ \(\sqrt{\frac{1.51}{V}}\)×10-9 = \(\sqrt{\frac{151}{V}}\)×10-10 ≒ \(\large{\frac{12.3}{\sqrt{V}}}\)×10-10 [m]
上式より電子線の波長は
電圧 \(V\) = 100 [V] で加速すると \(λ\) = 1.23×10-10 [m] になり、
電圧 \(V\) = 151 [V] で加速すると \(λ\) = 1.00×10-10 [m] になり、
電圧 \(V\) = 10000 [V] で加速すると \(λ\) = 1.23×10-11 [m] になり、
電圧 \(V\) = 15100 [V] で加速すると \(λ\) = 1.00×10-11 [m] になる、
とわかります。