接する物体
接する2物体
 なめらかな水平面上(あるいは宇宙空間)に、質量 m1、m2 の物体A、物体Bを接して置き、物体Aを水平方向(物体Aから物体Bの方向)に一定の力 F で押すときの運動について考えてみます。
なめらかな水平面上(あるいは宇宙空間)に、質量 m1、m2 の物体A、物体Bを接して置き、物体Aを水平方向(物体Aから物体Bの方向)に一定の力 F で押すときの運動について考えてみます。
このとき、物体Aと物体Bは接触したまま離れません*接触面が斜めだったりすれば、物体Aが物体Bを押し上げたりするでしょうが、そういうことは起こらないこととします。接触面は垂直であるとします。
閉じる。
 物体Aと物体Bが離れているところに力を加えれば、衝突が起こり、運動量が交換され、離ればなれになっていくでしょうが、
物体Aと物体Bが離れているところに力を加えれば、衝突が起こり、運動量が交換され、離ればなれになっていくでしょうが、
始めから接触していれば衝突が起こらないので、離ればなれになっていくことはありません。物体Bは慣性力を受けはしますが、離ればなれにはなりません。くっついたままです*地面に置かれた物体が、勝手に飛び上がることが無いのと一緒です。
閉じる。*力を加えるのをやめた後も離ればなれにはなりません。物体Aと物体Bの接触面には何の力もはたらかなくなりますが、接触したまま運動を続けます。
実際に実験した場合には、力を加えるのをやめた後は、2つの物体はゆっくり離ればなれになるでしょうが、それは物体Bにわずかながら弾性力があるためだと思います。
閉じる
くっついたままなので、2物体を1物体と見立てて運動方程式を立てることができます。加速度を a として、加えた力の方向を正としますと、
(m1 + m2) a = F
∴ a = \(\large{\frac{F}{m_1+m_2}}\)
これが物体A、物体Bの共通の加速度です。
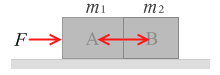 このとき、物体Aと物体Bの間には互いに押し合う作用・反作用の力がはたらいています。AがBを押し、Bが同じ力でAを押し返しているのです。作用・反作用の法則は加速している最中でも成り立ちます。
このとき、物体Aと物体Bの間には互いに押し合う作用・反作用の力がはたらいています。AがBを押し、Bが同じ力でAを押し返しているのです。作用・反作用の法則は加速している最中でも成り立ちます。
そしてここがポイントなのですが、この力は F と同じではありません。F より少し小さい力です。力 F はBに届くまでにAを加速するために使われて、目減りしています。目減りしてしまってはA、B両方を上で求めた a で加速させることができないと思われてしまうかもしれませんが、そうではありません。目減りした力はAとBを両方押すのではなく、Bだけを押すので大丈夫なのです。
力が目減りするのはおかしいと感じてしまうとすれば、それは力のつり合いと話がごちゃまぜになっているからです。確かに、力のつり合いを考えるときは力は目減りしません。
 しかし、力のつり合いを考えるときは物が動かないときです。(正確には物の速度が変わらないときです)。
しかし、力のつり合いを考えるときは物が動かないときです。(正確には物の速度が変わらないときです)。
力のつり合いを考えるときは加速度が 0 なので運動方程式は立てられません。今は加速度が 0 ではないので力はつり合っておらず、運動方程式を立てることができます。
そういうわけで、この目減りした、AとBの間にはたらく力を f とおき、この力の大きさを求めてみます。
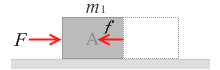 物体Aだけに着目して考えてみます。
物体Aだけに着目して考えてみます。
すると、物体Aについての運動方程式は、
m1 a = F - f
この式に上で求めた加速度 a = \(\large{\frac{F}{m_1+m_2}}\) を代入すると、
m1 \(\large{\frac{F}{m_1+m_2}}\) = F - f
∴ f = F - m1 \(\large{\frac{F}{m_1+m_2}}\)
= \(\large{\frac{(m_1+m_2)F\ }{m_1+m_2}}\) - m1 \(\large{\frac{F}{m_1+m_2}}\)
= \(\large{\frac{(m_1+m_2)F\ -\ m_1 F}{m_1+m_2}}\)
= \(\large{\frac{m_2}{m_1+m_2}}\) F ……①
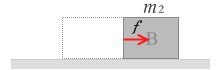 次に、物体Bだけに着目して考えてみます。
次に、物体Bだけに着目して考えてみます。
すると、物体Bについての運動方程式は、
m2 a = f
この式に上で求めた加速度 a = \(\large{\frac{F}{m_1+m_2}}\) を代入すると、
m2 \(\large{\frac{F}{m_1+m_2}}\) = f
∴ f = \(\large{\frac{m_2}{m_1+m_2}}\) F ……②
①式と②式は同一です。物体Aについての運動方程式を立てても、物体Bについての運動方程式を立てても、同じ f の値が導き出されます。
この式を解釈しますと、
 m1 » m2 のときは、f がほぼ 0 になり、
m1 » m2 のときは、f がほぼ 0 になり、
 m1 « m2 のときは、f がほぼ F になるということがいえます。
m1 « m2 のときは、f がほぼ F になるということがいえます。
ポイントをまとめます
- 物体が加速しているのなら、力のつり合いは成り立っておらず、力は1番目の物体を加速するために使われ、2番目の物体に伝わるまでに目減りする。
- 作用・反作用の法則は、いかなるときも成り立っている。
- 運動方程式は、全体をひとまとめにしたものと、各物体についてのものとを立てる。