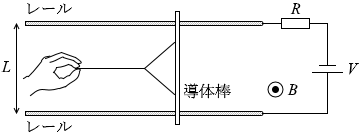
(問3)電流は磁場から力 を受けますが、その方向はフレミングの左手の法則 によって決まり*
磁束(磁場)の向きは紙面こちら向き です。
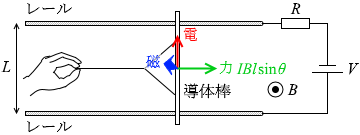
閉じる F = (IBl sinθ )
導体棒は静止しているので、この力と手の力はつり合っている ということであり、つまり手の力 F の大きさも (IBl sinθ ) ということです。
本問においては
(I ) ⇒ \(\large{\frac{V}{R}}\) (オームの法則 より。導体棒が動いていれば \(\large{\frac{V}{R}}\) ではありませんが)
(l ) ⇒ L
(sinθ ) ⇒ sin90° = 1
であるので、
F = (IBl sinθ ) = \(\large{\frac{VBL}{R}}\)
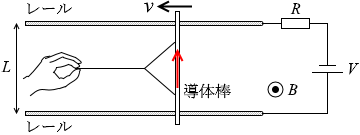
(問4)誘導起電力が発生 します。その大きさは
(V ) = (vBl ) = vBL
です。
向き はレンツの法則に従います。
紙面こちら向きの磁束(磁場)が増えるので、それを打ち消すために紙面向こう向きの磁束を増やすように右回りの誘導起電力が発生します。
キルヒホッフの第2法則 の式を立てますと、
V + vBL - RI = 0
∴ RI = V + vBL ……❶
∴ I = \(\large{\frac{V+vBL}{R}}\)
(問5)電力 には3通りの表現方法 P = (IV = I 2 R = \(\large{\frac{V^2}{R}}\)) がありますが抵抗に掛かる電圧はよく分からないので P = (I 2 R ) を採用することにして、❶式を代入しますと、
P = I × RI = I × (V + vBL ) = IV + IvBL ……❷
となり、次に、解答の選択肢に F が多く含まれているので F について考えてみますと、
(F = IBl sinθ ) の大きさの力を受けます。
本問においては
(F ) ⇒ (f と置く)
(I ) ⇒ I
(l ) ⇒ L
(sinθ ) ⇒ sin90° = 1
であるので、f = IBl です。
一定の速さで動いているので 、
F と f はつり合っています。つまり、F = IBL です。
これを❷式に代入しますと、
P = IV + IvBL = IV + Fv
となります。
答えは ④ です。
(分析)
P = IV + Fv
の右辺第1項 IV は導体棒が動かない場合の抵抗で消費される電力を表しています。
第2項の Fv は手のした仕事率を表しています。
導体棒は1秒間に v [m] 進みますが、手の力の大きさは F であるので、手が1秒間にする仕事の大きさは Fv ということになります 。1秒間にする仕事というのは仕事率 のことであり、仕事率というのは電力 に置き換えられます。手が発電 しているということです。
つまり上式は、抵抗で消費される電力は直流電源が発揮する電力と手が発揮する仕事率を合わせたもの、という意味になります。
そして、両辺に時間 t を掛ければエネルギー保存の法則 を表す式となります。
逆にいいますと、エネルギー保存則から抵抗の消費電力は直流電源による IV と手による Fv の和であるな、と暗算で導き出すことができます。
(良問)
 その
その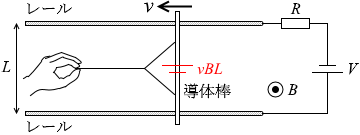 つまりこのような回路であるとみなせます。
つまりこのような回路であるとみなせます。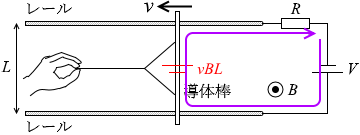 左図のような経路について右回りを正とする
左図のような経路について右回りを正とする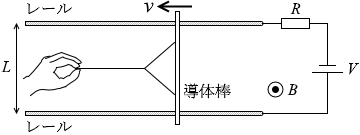 そして導体棒は
そして導体棒は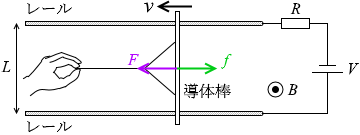 F と f はつり合っています。つまり、F = IBL です。
F と f はつり合っています。つまり、F = IBL です。