一様な電場、または一様な磁場の中で、正に帯電した粒子が平面内を運動した。図3に示すように、平面内の直線 l 上に距離 L だけ離れた2点P、Qがあり、粒子は、点Pを直線 l と 45° をなす方向に速さ v で通過した後、点Qを直線 l と 45° をなす方向に同じ速さ v で通過した。
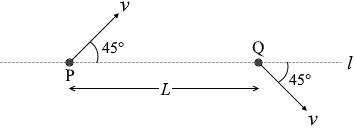
(問3)このとき、電場の向き、磁場の向きとして最も適当なものを、次の①~⑥のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
電場の場合:3
磁場の場合:4
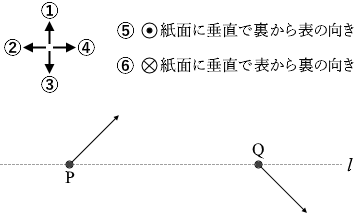
(問4)磁場の場合に、点Pから点Qまでの粒子の軌跡と、その間を運動するのに要した時間を表す式の組合せとして最も適当なものを、次の①~⑨のうちから一つ選べ。
| 軌跡 | 時間 | |
|---|---|---|
| ① | 放物線 | \(\large{\frac{\sqrt2πL}{4v}}\) |
| ② | 放物線 | \(\large{\frac{\sqrt2πL}{2v}}\) |
| ③ | 放物線 | \(\large{\frac{\sqrt2L}{v}}\) |
| ④ | 円弧 | \(\large{\frac{\sqrt2πL}{4v}}\) |
| ⑤ | 円弧 | \(\large{\frac{\sqrt2πL}{2v}}\) |
| ⑥ | 円弧 | \(\large{\frac{\sqrt2L}{v}}\) |
| ⑦ | 双曲線 | \(\large{\frac{\sqrt2πL}{4v}}\) |
| ⑧ | 双曲線 | \(\large{\frac{\sqrt2πL}{2v}}\) |
| ⑨ | 双曲線 | \(\large{\frac{\sqrt2L}{v}}\) |
#センター16本試物理
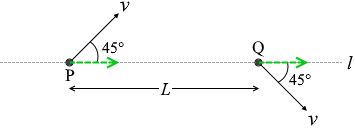 粒子の運動の l 方向の成分には変化が無く、
粒子の運動の l 方向の成分には変化が無く、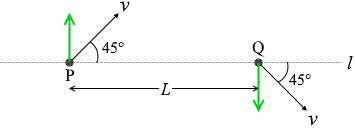 l と垂直な方向の成分だけが変化しています。
l と垂直な方向の成分だけが変化しています。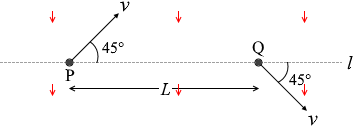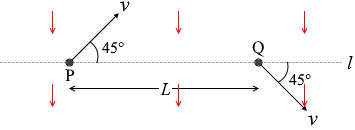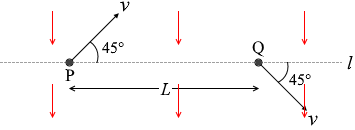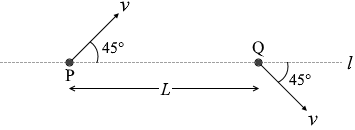 電場の向きは紙面下向きです。
電場の向きは紙面下向きです。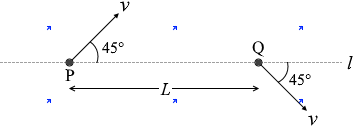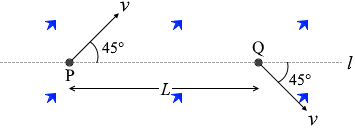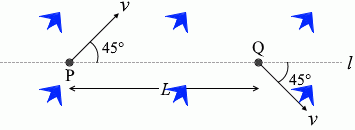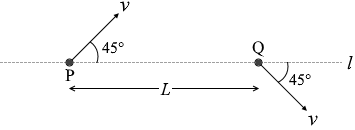 答えは ⑤
答えは ⑤ 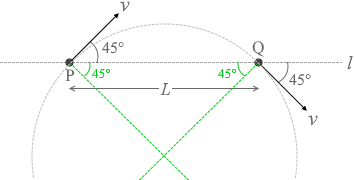 それは運動方向と垂直の方向にあるはずだから、左図の2つの緑線の交点が円の中心となっているはずです。
それは運動方向と垂直の方向にあるはずだから、左図の2つの緑線の交点が円の中心となっているはずです。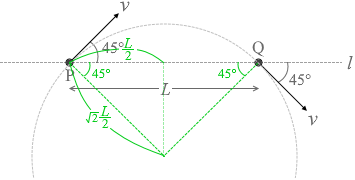 そして、円の半径が \(\large{\frac{\sqrt2L}{2}}\)
そして、円の半径が \(\large{\frac{\sqrt2L}{2}}\) 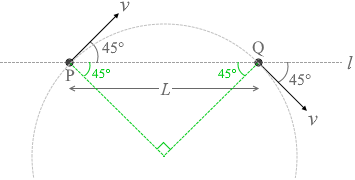 円弧 \(\stackrel{\frown}{\rm{PQ}}\) の長さは円周の (\(\large{\frac{90°}{360°}}\)=) \(\large{\frac{1}{4}}\) であるので、
円弧 \(\stackrel{\frown}{\rm{PQ}}\) の長さは円周の (\(\large{\frac{90°}{360°}}\)=) \(\large{\frac{1}{4}}\) であるので、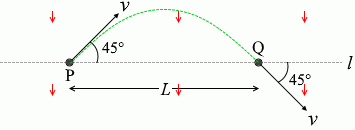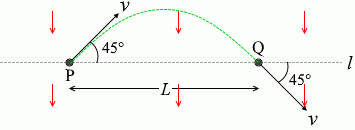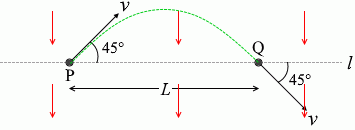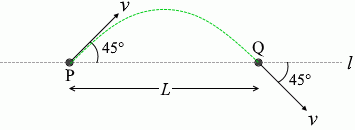 粒子の軌跡は放物線となります。重力空間における
粒子の軌跡は放物線となります。重力空間における