（問1）
惑星と恒星の間の万有引力の大きさは
G\(\large{\frac{mM}{r^2}}\)
『万有引力の法則』において
G\(\large{\frac{Mm}{r^2}}\)
と表現したものを、ここでは
G\(\large{\frac{mM}{r^2}}\)
としていますがこれは、問題文の問5の m と M の順番に合わせただけで
特に意味はありません。
\(\large{\frac{MmG}{r^2}}\)
としたって間違いではありません。
等速円運動する惑星の加速度は
\(\large{\frac{v^2}{r}}\)
よって、運動方程式（ma = F）は
m\(\large{\frac{v^2}{r}}\) = G\(\large{\frac{mM}{r^2}}\)
∴ v2 = G\(\large{\frac{M}{r}}\)
∴ v = \(\large{\sqrt{\frac{GM}{\large{r}}}}\)
万有引力 G\(\large{\frac{mM}{r^2}}\) が
半径 r の等速円運動の向心力となるから、
m\(\large{\frac{v^2}{r}}\) = G\(\large{\frac{mM}{r^2}}\)
と考えてもいいです。
（問2）
この惑星の運動エネルギーは
\(\large{\frac{1}{2}}\)mv2
この惑星の万有引力による位置エネルギーは
- G\(\large{\frac{mM}{r}}\)
よって力学的エネルギー（運動エネルギー + 位置エネルギー）は
\(\large{\frac{1}{2}}\)mv2 + \(\big(\)- G\(\large{\frac{mM}{r}}\)\(\big)\) 問1の結果を代入して
= \(\large{\frac{1}{2}}\)m\(\large{\frac{GM}{r}}\) - G\(\large{\frac{mM}{r}}\)
= \(\big(\)\(\large{\frac{1}{2}}\) - 1\(\big)\)\(\large{\frac{GmM}{r}}\)
= - \(\large{\frac{GmM}{2r}}\)
（3種のエネルギーの大きさ比べ）
問1の結果を運動エネルギーの式に代入しますと、
\(\large{\frac{GmM}{2r}}\)
位置エネルギーは
- G\(\large{\frac{mM}{r}}\)
力学的エネルギーは
- \(\large{\frac{GmM}{2r}}\)
であるので、絶対値の大きさを比べると 1:2:1 になっています。
（問3）
周期というのは（1周の長さ）÷（周回する速さ）であるから、
T = \(\large{\frac{2πr}{v}}\) 両辺2乗しますと
∴ T2 = \(\large{\frac{4π^2r^2}{v^2}}\) 問1の結果を代入しますと
∴ T2 = 4π2r2\(\large{\frac{r}{GM}}\)
= \(\large{\frac{4π^2}{GM}}\)r3
T と r のこの関係はケプラーの第3法則を表しています。
（問4）
恒星から最も離れたときの惑星の速さを v2 と置きます。そうしますと、ケプラーの第2法則より、
\(\large{\frac{1}{2}}\)r1v1 = \(\large{\frac{1}{2}}\)r2v2
∴ v2 = \(\large{\frac{r_1}{r_2}}\)v1 ……①
最も近づいたときの惑星の力学的エネルギーは
\(\large{\frac{1}{2}}\)mv12 + (- G\(\large{\frac{mM}{r_1}}\))
問2の結果
- \(\large{\frac{GmM}{2r}}\)
に代入するのは間違いです。
問2は円運動、問4は楕円運動です。
……②
最も離れたときの惑星の力学的エネルギーは
\(\large{\frac{1}{2}}\)mv22 + (- G\(\large{\frac{mM}{r_2}}\))
力学的エネルギー保存の法則より、
\(\large{\frac{1}{2}}\)mv12 + (- G\(\large{\frac{mM}{r_1}}\)) = \(\large{\frac{1}{2}}\)mv22 + (- G\(\large{\frac{mM}{r_2}}\))
∴ \(\large{\frac{1}{2}}\)v12 - G\(\large{\frac{M}{r_1}}\) = \(\large{\frac{1}{2}}\)v22 - G\(\large{\frac{M}{r_2}}\) ①式を代入して
∴ \(\large{\frac{1}{2}}\)v12 - G\(\large{\frac{M}{r_1}}\) = \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{r_1}^2}{{r_2}^2}}\)v12 - G\(\large{\frac{M}{r_2}}\)
∴ \(\large{\frac{1}{2}}\)v12 - \(\large{\frac{1}{2}}\)⋅\(\large{\frac{{r_1}^2}{{r_2}^2}}\)v12 = G\(\large{\frac{M}{r_1}}\) - G\(\large{\frac{M}{r_2}}\)
∴ \(\large{\frac{1}{2}}\)\(\big(\)1 - \(\large{\frac{{r_1}^2}{{r_2}^2}}\)\(\big)\)v12 = \(\big(\)\(\large{\frac{1}{r_1}}\) - \(\large{\frac{1}{r_2}}\)\(\big)\)GM
∴ \(\big(\)1 - \(\large{\frac{{r_1}^2}{{r_2}^2}}\)\(\big)\)v12 = 2\(\big(\)\(\large{\frac{1}{r_1}}\) - \(\large{\frac{1}{r_2}}\)\(\big)\)GM
∴ \(\large{\frac{{r_2}^2-{r_1}^2}{{r_2}^2}}\)v12 = 2\(\large{\frac{r_2-r_1}{r_1r_2}}\)GM
∴ \(\large{\frac{(r_2+r_1)(r_2-r_1)}{r_2}}\)v12 = 2\(\large{\frac{r_2-r_1}{r_1}}\)GM
∴ \(\large{\frac{(r_2+r_1)}{r_2}}\)v12 = 2\(\large{\frac{1}{r_1}}\)GM
∴ v12 = 2\(\large{\frac{r_2}{r_1(r_2+r_1)}}\)GM
∴ v1 = \(\large{\sqrt{\frac{2GMr_2}{r_1(r_1+r_2)}}}\)
r1 = r2 のときは \(\large{\frac{2r_2}{(r_2+r_1)}}\) = 1 であり、
v1 = \(\large{\sqrt{\frac{GM}{r_1}}}\)
となり、問1の円運動の場合と一致します。
（問5）
惑星の力学的エネルギーは（問4の結果を②式に入れ戻して
②式の下の
「最も離れたときの惑星の力学的エネルギー」の式に
①式と共に入れ戻してもいいです。同じです。
）
\(\large{\frac{1}{2}}\)mv12 + (- G\(\large{\frac{mM}{r_1}}\))
= \(\large{\frac{1}{2}}\)m×\(\large{\frac{2GMr_2}{r_1(r_1+r_2)}}\) + (- G\(\large{\frac{mM}{r_1}}\))
= m×\(\large{\frac{GMr_2}{r_1(r_1+r_2)}}\) - G\(\large{\frac{mM}{r_1}}\)
= \(\Big\{\)\(\large{\frac{r_2}{r_1(r_1+r_2)}}\) - \(\large{\frac{(r_1+r_2)}{r_1(r_1+r_2)}}\)\(\Big\}\)GmM
= \(\Big\{\) - \(\large{\frac{r_1}{r_1(r_1+r_2)}}\)\(\Big\}\)GmM
= - \(\large{\frac{GmM}{r_1+r_2}}\)
ところで、
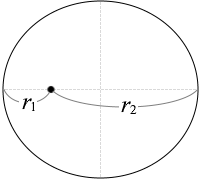r1 と r2 を足したものが楕円の長軸 2a になるから、
r1 + r2 = 2a
これを上式に代入すると、惑星の力学的エネルギーは
- \(\large{\frac{GmM}{2a}}\)
と表せます。
r1 = r2 のとき、つまり円のとき、上式は
- \(\large{\frac{GmM}{2r_1}}\)
となり、問2の結果と一致します。