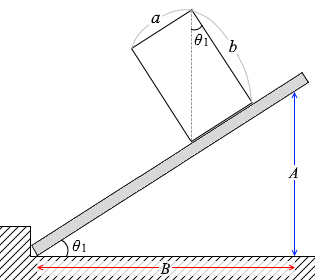
図3のように、直径 a 、高さ b の円柱をあらい板の上に置き、板の一端をゆっくり持ち上げる。このとき、円柱が滑らずに転倒する条件として最も適当なものを、下の①~⑥のうちから一つ選べ。ただし、円柱と板の間の静止摩擦係数を μ とし、円柱の密度は一様であるものとする。
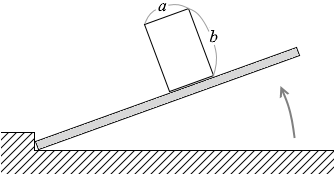
① a > μb ② b > μa ③ ab > μ
④ a < μb ⑤ b < μa ⑥ ab < μ
#センター16追試物理
図3のように、直径 a 、高さ b の円柱をあらい板の上に置き、板の一端をゆっくり持ち上げる。このとき、円柱が滑らずに転倒する条件として最も適当なものを、下の①~⑥のうちから一つ選べ。ただし、円柱と板の間の静止摩擦係数を μ とし、円柱の密度は一様であるものとする。

① a > μb ② b > μa ③ ab > μ
④ a < μb ⑤ b < μa ⑥ ab < μ
#センター16追試物理
円柱が滑らないためには μ が大きい方がいいだろうし、転倒するには a が小さくて b が大きい方がいいはずだから、答えは④とすぐにわかります。選択肢問題だからこのようにして解けばいいのですが、一応ちゃんと説明してみます。
物体が滑るか滑らないかについては『摩擦角』項で詳しく解説したのでそちらを読んでいただくとして、物体が転倒するというのはどういうことかを考えてみます。
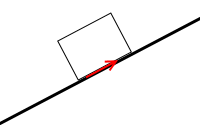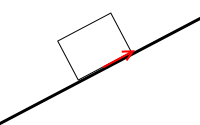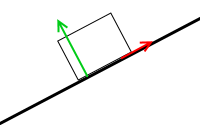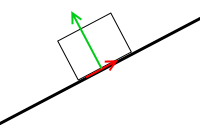
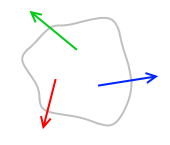 転倒するということは回転するということであり、回転してしまうということは力のモーメントがつり合っていないということであり、たとえば左図のような力の掛かり方をしているということです。(物体は左回りに回転してしまう)
転倒するということは回転するということであり、回転してしまうということは力のモーメントがつり合っていないということであり、たとえば左図のような力の掛かり方をしているということです。(物体は左回りに回転してしまう)
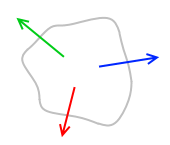 左図のような力の掛かり方であれば力のモーメントはつり合い、物体は回転しません。
左図のような力の掛かり方であれば力のモーメントはつり合い、物体は回転しません。
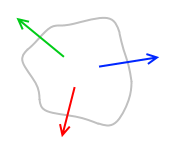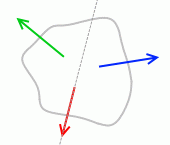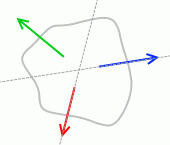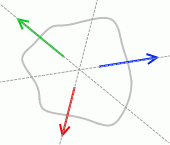 力のモーメントがつり合うときは3力の作用線は1点で交わります。交わらないときは力のモーメントはつり合いません。
力のモーメントがつり合うときは3力の作用線は1点で交わります。交わらないときは力のモーメントはつり合いません。
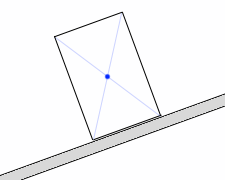 本問の場合、
本問の場合、
円柱の重心はその真ん中であり、
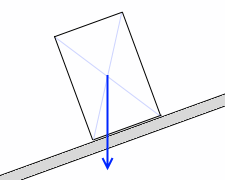 そこに重力が掛かっています。
そこに重力が掛かっています。
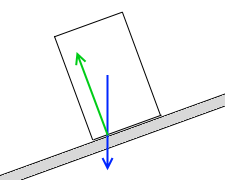 板の上に置かれているので垂直抗力を受け、
板の上に置かれているので垂直抗力を受け、
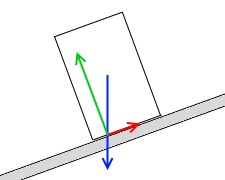 あらい板であるので、摩擦力がはたらき、
あらい板であるので、摩擦力がはたらき、
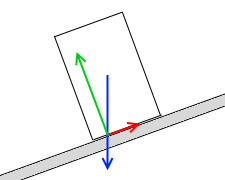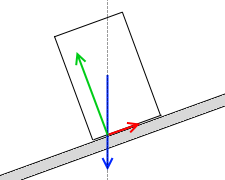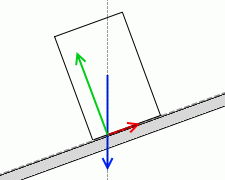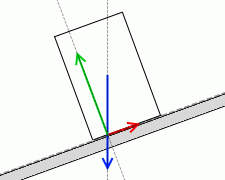 円柱が転倒しないときは、これらの力のモーメントがつり合っています。
円柱が転倒しないときは、これらの力のモーメントがつり合っています。
力のモーメントがつり合っているということはそれらの作用線が1点で交わるということであり、
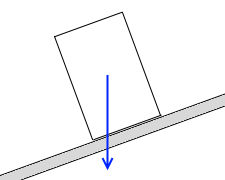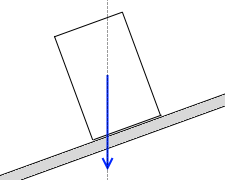 重力の作用線は円柱の重心を通る鉛直線であり、
重力の作用線は円柱の重心を通る鉛直線であり、
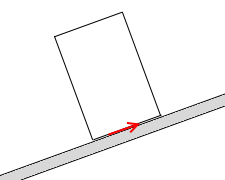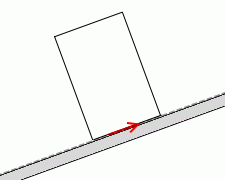 摩擦力の作用線は斜面内にあるので、
摩擦力の作用線は斜面内にあるので、
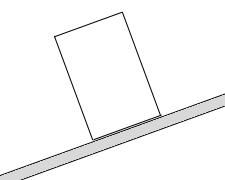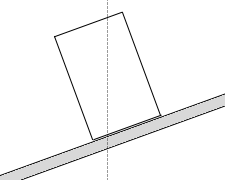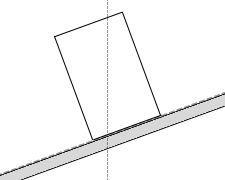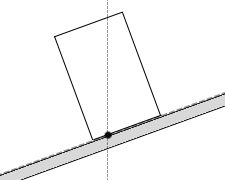 作用線が交わる点というのは”重力の作用線と斜面の交点”、ということになります。
作用線が交わる点というのは”重力の作用線と斜面の交点”、ということになります。
垂直抗力の作用線もここを通るわけですが、その作用点は必ず斜面上のどこかにある
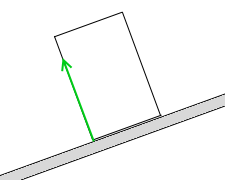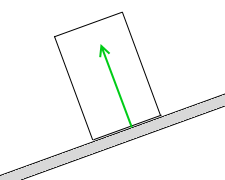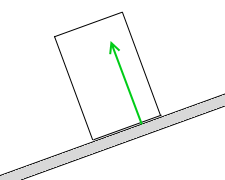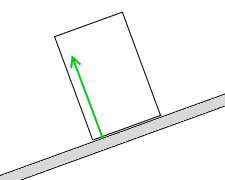 わけですから、自動的に垂直抗力の作用点は”重力の作用線と斜面の交点”ということになります。
わけですから、自動的に垂直抗力の作用点は”重力の作用線と斜面の交点”ということになります。
 そして、これよりも斜面が傾くと重力の作用線は垂直抗力や摩擦力の作用点から外れてしまいます
そして、これよりも斜面が傾くと重力の作用線は垂直抗力や摩擦力の作用点から外れてしまいます
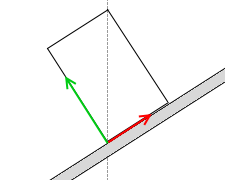 垂直抗力の作用点と摩擦力の作用点は
垂直抗力の作用点と摩擦力の作用点は
円柱の底面内に留まります。
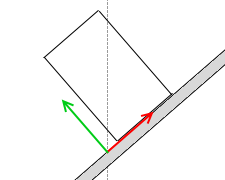 底面から外れたらおかしいです。
。3つの力の作用線が1点で交わらなくなります。力のモーメントがつり合わなくなり、円柱が転倒し始めます。重心の位置が円柱の最下点より左に来ると、円柱が斜面から浮き上がって転倒し始めるということです。
底面から外れたらおかしいです。
。3つの力の作用線が1点で交わらなくなります。力のモーメントがつり合わなくなり、円柱が転倒し始めます。重心の位置が円柱の最下点より左に来ると、円柱が斜面から浮き上がって転倒し始めるということです。
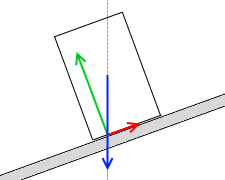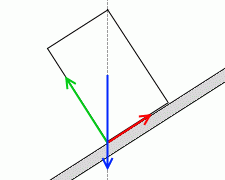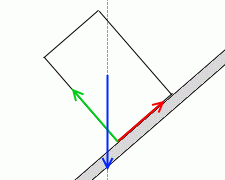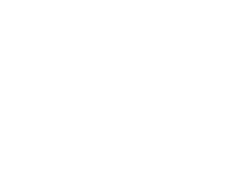
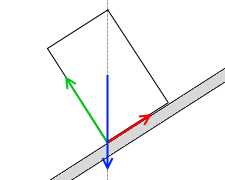 つまり、”重力の作用線と斜面の交点”が底面のちょうど最下点にきたときが円柱が転倒するかどうかの境目です。
つまり、”重力の作用線と斜面の交点”が底面のちょうど最下点にきたときが円柱が転倒するかどうかの境目です。
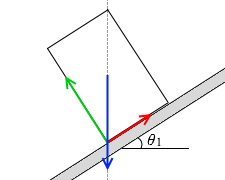 このときの斜面の仰角を θ1 とします。
このときの斜面の仰角を θ1 とします。
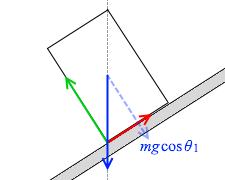 そうしますと、このとき斜面に押し付ける力の大きさは mgcosθ1 であり、
そうしますと、このとき斜面に押し付ける力の大きさは mgcosθ1 であり、
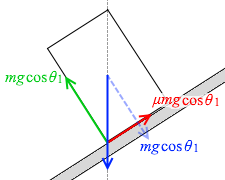 つまり、垂直抗力の大きさは mgcosθ1 であり、最大静止摩擦力はそれに μ を掛けた μmgcosθ1 です。
つまり、垂直抗力の大きさは mgcosθ1 であり、最大静止摩擦力はそれに μ を掛けた μmgcosθ1 です。
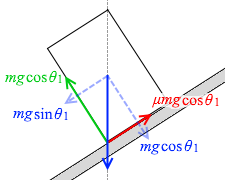 斜面下に滑り落とそうとする力は mgsinθ1 であるので、
斜面下に滑り落とそうとする力は mgsinθ1 であるので、
円柱が滑らないための条件は
μmgcosθ1 > mgsinθ1
∴ μ > \(\large{\frac{\sinθ_1}{\cosθ_1}}\)
∴ μ > tanθ1 ……❶
です。
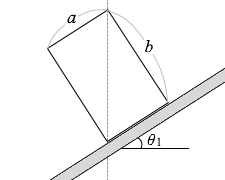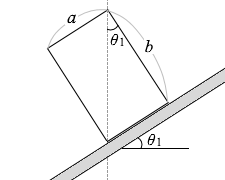 このときの θ1 は円柱のここの角度でもあるので、
このときの θ1 は円柱のここの角度でもあるので、
tanθ1 = \(\large{\frac{a}{b}}\)
です。
これを❶式に代入して θ1 を含まない式にしますと、
μ > \(\large{\frac{a}{b}}\)
∴ a < μb
となります。
斜面の角度を徐々に大きくしていって θ1 となるまで摩擦力が勝っていてくれれば、それより角度が大きくなった瞬間に円柱の転倒が始まります。静止摩擦係数 μ が \(\large{\frac{a}{b}}\) より大きければ円柱は θ1 まで踏ん張ることができ、θ1 より大きく傾いた瞬間、重心の位置が底面の最下点の位置より左に来て、自然と転倒が始まるということです。
(式を解釈)
 \(\large{\frac{a}{b}}\) というのは左図の \(\large{\frac{A}{B}}\) と同じであり、θ1 というのは摩擦角のことであり、tanθ1 は \(\large{\frac{A}{B}}\) のことであり、つまりは円柱が摩擦角の比より細長ければ、滑らずに転倒するということです。
\(\large{\frac{a}{b}}\) というのは左図の \(\large{\frac{A}{B}}\) と同じであり、θ1 というのは摩擦角のことであり、tanθ1 は \(\large{\frac{A}{B}}\) のことであり、つまりは円柱が摩擦角の比より細長ければ、滑らずに転倒するということです。
それほど細長くない場合は、転倒せずに滑り落ちていきます。そのときの条件は符号の向きが逆になって、
a > μb
となります。
a = μb のときはどうなるか分かりませんが、
円柱の最下点のみが斜面と接触しながら落ちていく
なんてことが起こるかもしれません。
(余談:なぜ円柱なのか)
円柱ではなく直方体であっても重心はその中心にあるので問題の設定として使うことができるのですが、直方体だとヨー方向(Wikipedia)に回転したときに a の長さが変わってしまうので、そのことをことわる必要が出てきます。
(余談:やじろべえ)
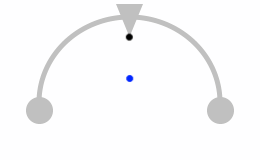 やじろべえが倒れないのは、重心が支点より下にあるからです。
やじろべえが倒れないのは、重心が支点より下にあるからです。
 やじろべえには重力がはたらくわけですが、
やじろべえには重力がはたらくわけですが、
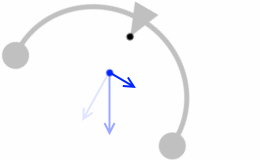 右に傾くと左に戻そうとする力がはたらき、
右に傾くと左に戻そうとする力がはたらき、
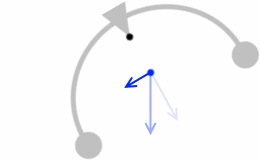 左に傾くと右に戻そうとする力がはたらきます。
左に傾くと右に戻そうとする力がはたらきます。
重心が支点より下にあればどんな形でもやじろべえになりえます。
物が転倒するかどうかを考えるときは、支点と重心の位置関係がポイントになります。
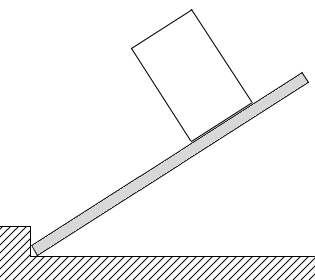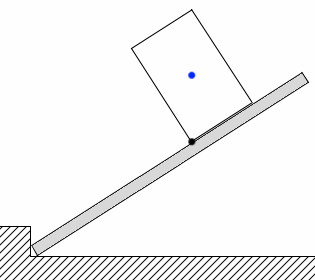 本問でいえば、円柱の最下点と円柱の中心の位置関係がポイントです。
本問でいえば、円柱の最下点と円柱の中心の位置関係がポイントです。
(余談:回転運動か並進運動か)
 多くの試験問題では転倒するかどうかは問わず、斜面方向にどのような運動をするかを問います。回転運動ではなく並進運動について問います。
多くの試験問題では転倒するかどうかは問わず、斜面方向にどのような運動をするかを問います。回転運動ではなく並進運動について問います。
 このようなときは作用点はいい加減でも大丈夫です。
このようなときは作用点はいい加減でも大丈夫です。
しかし回転運動が問われる場合は作用点の位置について厳密さが求められます。
(余談:改めて作用点について考えてみる)
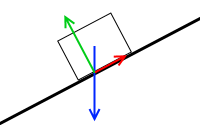 物体にはたらく力は重力、摩擦力、垂直抗力の3つで、作用点は左図のような位置ですが、
物体にはたらく力は重力、摩擦力、垂直抗力の3つで、作用点は左図のような位置ですが、
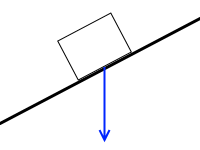 物体が板を押す力の作用点は、ここではなく、
物体が板を押す力の作用点は、ここではなく、
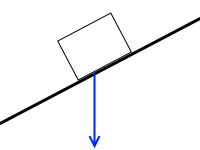 ここです。
ここです。
 この力の板に垂直な成分の作用点は、ここではなく、
この力の板に垂直な成分の作用点は、ここではなく、
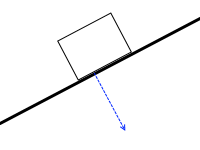 ここです。”重力の作用線と斜面の交点”です。
ここです。”重力の作用線と斜面の交点”です。
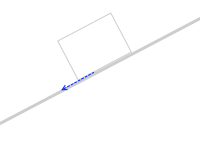 板に平行な成分の様子は、こうです。
板に平行な成分の様子は、こうです。
”あらい板”ではなく”なめらかな板”の場合であっても同じです。
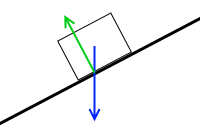 物体にはたらく力は重力と垂直抗力の2つで、
物体にはたらく力は重力と垂直抗力の2つで、
物体は転倒せず斜面に沿って落ちていき、
板が受ける力は垂直成分だけであり、
その作用点は
 ここではなく、
ここではなく、
 ここです。
ここです。
押す力の作用点が底面の真ん中ではないことを別の視点で考えてみます。
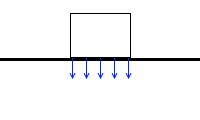 たとえば底面を5分割したとします。
たとえば底面を5分割したとします。
水平であれば均等に力が掛かりますが、
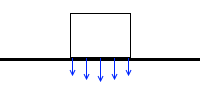
物体が円筒だとすると本当はこうなりますが、まあそれは置いといて、、、
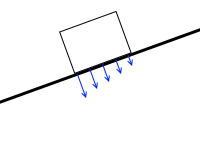 斜めになったときは斜面への力の掛かり方に強弱が生まれます。
斜めになったときは斜面への力の掛かり方に強弱が生まれます。
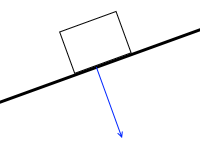 この5つの力を1つにまとめたときの合力の作用点は真ん中ではありません。斜めになるほど端に寄っていきます。それが”重力の作用線と斜面の交点”ということです。
この5つの力を1つにまとめたときの合力の作用点は真ん中ではありません。斜めになるほど端に寄っていきます。それが”重力の作用線と斜面の交点”ということです。
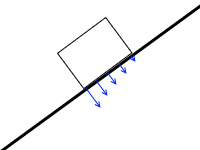 さらに傾斜させていくと
さらに傾斜させていくと
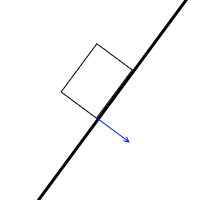 やがて、最下点の一点だけに力が掛かるようになります。”重力の作用線と斜面の交点”が底面のちょうど最下点にきたときであり、
やがて、最下点の一点だけに力が掛かるようになります。”重力の作用線と斜面の交点”が底面のちょうど最下点にきたときであり、
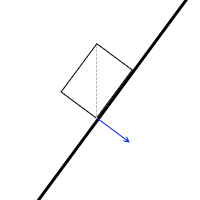 重力の作用線と物体の対角線が重なったときです。
重力の作用線と物体の対角線が重なったときです。
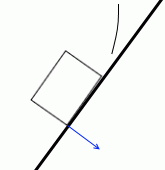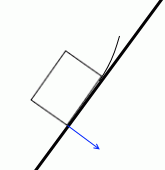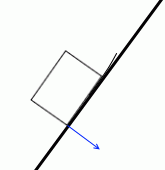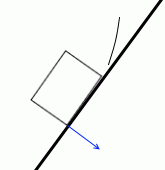 ここの隙間に紙が差し込めるような状態です。
ここの隙間に紙が差し込めるような状態です。
あるいは、
 円柱をたとえば12分割して考えたときに、
円柱をたとえば12分割して考えたときに、
クリスマスツリーの飾り付けの左右のバランスがとれたような状態です。