□
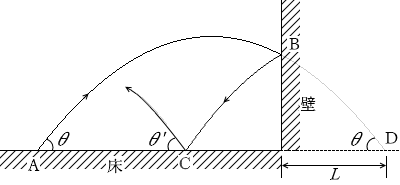
図2のように、水平な床の点Aから、垂直に立てられた壁に向かって角度 θ で質量 m の小球が打ち出された。小球は最高点に達した後、壁面上の点Bではね返り、床の点Cに落ちて角度 θ' の方向にはね上がった。ただし、床、壁は共に滑らかで、小球に対するはねかえり係数(反発係数)の大きさを共に e とする。また、壁がないときの小球の到達位置Dと壁との間の距離を L とする。
図 2
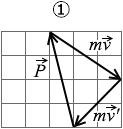
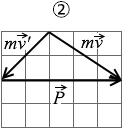
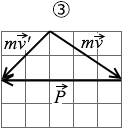
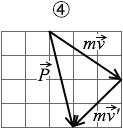
(問4)壁に衝突する直前の小球の運動量ベクトルを m \(\vec{v}\) とすると、衝突直後の小球の運動量ベクトル m \(\vec{v'}\) と壁が小球に加えた力積 \(\vec{P}\) の関係はどうなるか。最も適当なものを、次の①~④のうちから一つ選べ。
(問5)点Cから壁までの水平距離はいくらか。
(問6)tanθ' は tanθ の何倍か。
#センター04追試
壁は滑らか であるので摩擦が無く、鉛直方向には力積を与えません。力積は水平方向であり、左向きです。よって最も適当なグラフは ③ です。
運動量と力積 の関係を式で表せば、
m \(\vec{v'}\) - m \(\vec{v}\) = \(\vec{P}\)
となりますが、ベクトルからベクトルを引くときは 、基準となるベクトルの先端から対象となるベクトルの先端へ矢印を引くので、正しい図は ③ です。
(余談)m \(\vec{v}\) + m \(\vec{v'}\) = - \(\vec{P}\)
②図を式で表すと m \(\vec{v}\) - m \(\vec{v'}\) = \(\vec{P}\)
④図を式で表すと m \(\vec{v}\) + m \(\vec{v'}\) = \(\vec{P}\)
θ 、θ' というのは小球の軌跡の角度であり、速度の角度のことであります。
そして tan θ 、tanθ' というのは \(\frac{速度の鉛直成分の大きさ}{速度の水平成分の大きさ}\) のことです。
・速度の水平成分の大きさは、点Bにおいて e 倍に小さくなります。このとき鉛直成分は変化しません。
・速度の鉛直成分については、鉛直上方投射 の運動*
『斜方投射1 』項参照。
閉じる e 倍に小さくなります。このとき水平成分は変化しません。
つまり、点Bでのはね返りで水平成分が e 倍に小さくなり、点Cでのはね返りで鉛直成分が e 倍に小さくなり、トータルで \(\large{\frac{e}{e}}\) 倍、すなわち 1倍 になります。
(余談)e で、床でのはねかえり係数が e' であれば、トータルでは \(\large{\frac{e'}{e}}\) 倍となります。
さらにもう一度はねかえり係数 e の壁ではね返ればトータルでは \(\large{\frac{e'}{e^2}}\) 倍となります。
↑
↓
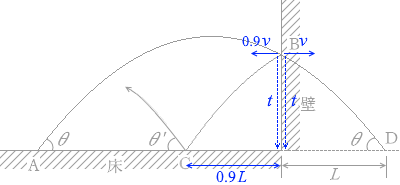 たとえば e = 0.9 なら 0.9L です。
たとえば e = 0.9 なら 0.9L です。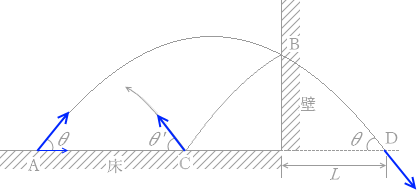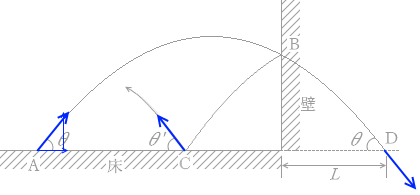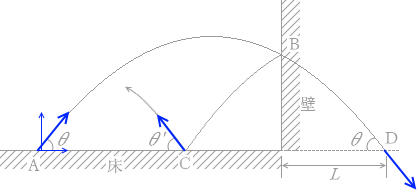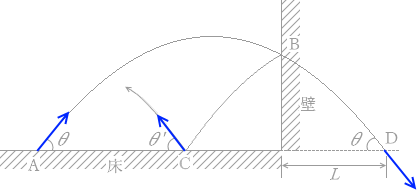 θ 、θ' というのは小球の軌跡の角度であり、速度の角度のことであります。
θ 、θ' というのは小球の軌跡の角度であり、速度の角度のことであります。