（問1）mg だけです。
運動方向成分 は、mg sinθ です。
斜面方向（運動方向）の加速度を a として運動方程式 を立てますと、
ma = mg sinθ
∴ a = g sinθ
この加速度は暗算で導き出してもかまいません。
物体はこの加速度で等加速度直線運動 をするから、求める時間を t と置いて変位の式を立てると、
l = 0⋅t + \(\large{\frac{1}{2}}\)⋅g sinθ ⋅t 2
∴ g sinθ ⋅t 2 = 2l
∴ t = \(\sqrt{\large{\frac{2l}{g\sinθ}}}\)
（問2）＊
下の問3で説明しますが、本問では一部区間で単振動をします。
閉じる ばね振り子の力学的エネルギー 』項では、ばねにつながれたおもりを引っ張ること（弾性エネルギー）によって動かし始めましたが、本問では、初速を与えること（運動エネルギー）によって動かし始めています。どちらの場合も摩擦が無ければエネルギーは保存します。
そして、単振動 においては最も速さ が速いのは振動の中心です。つまり、この物体は点Cを中心に単振動をします。そして単振動の中心においては加速度 が 0 です。加速度が 0 ということは力の合力が 0 ということです。点Cにおいては、ばねの弾性力と重力の斜面方向成分がつり合っているのです。
求める距離を l C としますと、点Cでの弾性力 は k (l C - l ) です。
ですので、
mg sinθ = k (l C - l )
∴ (l C - l ) = \(\large{\frac{mg}{k}}\)sinθ
∴ l C = l +\(\large{\frac{mg}{k}}\)sinθ
（別解：点Cでの速さを式で表してそれが最大となる条件を求める）v C として、点Cを基準とするエネルギーの式 を立てます。
（A点での力学的エネルギー）=（A点での運動エネルギー）+（A点での重力による位置エネルギー）+（A点での弾性エネルギー）
= ( 0 ) + ( mgl C sinθ ) + ( 0 )
= mgl C sinθ ……➊
（C点での力学的エネルギー）=（C点での運動エネルギー）+（C点での重力による位置エネルギー）+（C点での弾性エネルギー）
= ( \(\large{\frac{1}{2}}\)mv C 2 ) + ( 0 ) + ( \(\large{\frac{1}{2}}\)k (l C - l )2 )
= \(\large{\frac{1}{2}}\)mv C 2 + \(\large{\frac{1}{2}}\)k (l C - l )2 ……➋
力学的エネルギー保存の法則 により ➊ = ➋ であるから、
\(\large{\frac{1}{2}}\)mv C 2 + \(\large{\frac{1}{2}}\)k (l C - l )2 =mgl C sinθ
v C を l C の2次関数とみなして平方完成の形に持っていくと、
v C 2 + \(\large{\frac{k}{m}}\)(l C - l )2 = 2gl C sinθ
∴ v C 2 = - \(\large{\frac{k}{m}}\)(l C - l )2 + 2gl C sinθ
= - \(\large{\frac{k}{m}}\)(l C 2 - 2ll C + l 2 ) + 2gl C sinθ
= - \(\large{\frac{k}{m}}\)(l C 2 - 2ll C - 2\(\large{\frac{mg}{k}}\)l C sinθ + l 2 )
= - \(\large{\frac{k}{m}}\)\(\biggl\{\)l C 2 - 2\(\Big(\)l + \(\large{\frac{mg}{k}}\)sinθ \(\Big)\)l C + l 2 \(\biggr\}\)
= - \(\large{\frac{k}{m}}\)\(\biggl\{\)l C 2 - 2\(\Big(\)l + \(\large{\frac{mg}{k}}\)sinθ \(\Big)\)l C + \(\Big(\)l + \(\large{\frac{mg}{k}}\)sinθ \(\Big)\)2 - \(\Big(\)l + \(\large{\frac{mg}{k}}\)sinθ \(\Big)\)2 + l 2 \(\biggr\}\)
= - \(\large{\frac{k}{m}}\)\(\biggl\{\)l C 2 - 2\(\Big(\)l + \(\large{\frac{mg}{k}}\)sinθ \(\Big)\)l C + \(\Big(\)l + \(\large{\frac{mg}{k}}\)sinθ \(\Big)\)2 - \(\Big(\)l 2 + 2\(\large{\frac{lmg}{k}}\)sinθ + (\(\large{\frac{mg}{k}}\)sinθ )2 \(\Big)\) + l 2 \(\biggr\}\)
= - \(\large{\frac{k}{m}}\)\(\biggl\{\)l C 2 - 2\(\Big(\)l + \(\large{\frac{mg}{k}}\)sinθ \(\Big)\)l C + \(\Big(\)l + \(\large{\frac{mg}{k}}\)sinθ \(\Big)\)2 - 2\(\large{\frac{lmg}{k}}\)sinθ - (\(\large{\frac{mg}{k}}\)sinθ )2 \(\biggr\}\)
= - \(\large{\frac{k}{m}}\)\(\biggl\{\)l C 2 - 2\(\Big(\)l + \(\large{\frac{mg}{k}}\)sinθ \(\Big)\)l C + \(\Big(\)l + \(\large{\frac{mg}{k}}\)sinθ \(\Big)\)2 \(\biggr\}\) + 2lg sinθ + \(\large{\frac{mg^2}{k}}\)sin2 θ
= - \(\large{\frac{k}{m}}\)\(\biggl\{\)l C - \(\Big(\)l + \(\large{\frac{mg}{k}}\)sinθ \(\Big)\)\(\biggr\}\)2 + 2lg sinθ + \(\large{\frac{mg^2}{k}}\)sin2 θ
よって v C が最大になるのは
l C = l +\(\large{\frac{mg}{k}}\)sinθ
のとき。
（問3）保存 され続けます。摩擦が無いからです。
本問における力学的エネルギーというのは、重力による位置エネルギー とばねの弾性力による位置エネルギー と運動エネルギー のことです。この3つのエネルギーの総和がずっと保存されているのです。
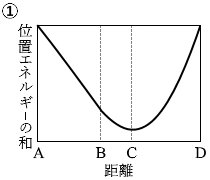
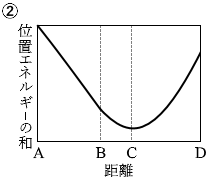
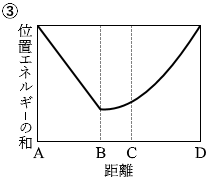
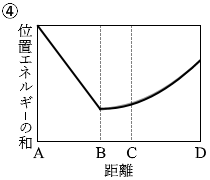
点Aと点Dでは物体の速さは 0 です。つまり、運動エネルギー が 0 です。ということは、点Aと点Dでは、重力による位置エネルギー とばねの弾性力による位置エネルギー の和が最大であり等しいということになります。このことを表しているグラフは①か③です。
さらに、物体の速さが最大となるのは点Cです。運動エネルギー が最大ということです。ということは、点Cでは、重力による位置エネルギー とばねの弾性力による位置エネルギー の和が最小ということになります。このことを表しているグラフは①か②です。
というわけで答えは ① です。
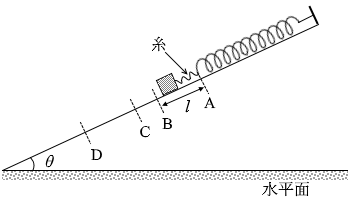
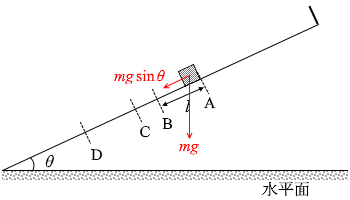はじめ、糸はたるんでいるので張力は 0 であり、物体にかかる力は mg だけです。
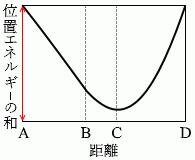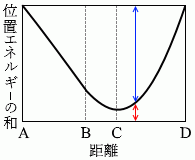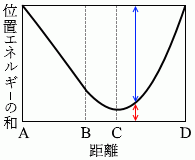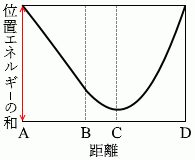点Aから点Bまでの曲線は直線で、点Bから点Dまでの曲線は放物線です。物体は点Aと点Dを往復します。点Bから点Dの間は単振動と同じ動きをします。
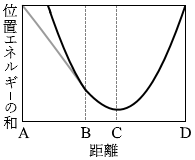もし糸が無く、物体が直接ばねに取り付けられていれば、曲線は完全な放物線になります。