水平面と角度 θ をなす、なめらかな斜面上の物体の運動を考える。重力加速度の大きさを g とする。
小物体を斜面上の点Pから斜面に沿って上向きに速さ v0 で打ち出したところ、図2のように小物体は斜面を上り、点Pから L だけ離れた点Qを速さ v で通過した。v を式で表わせ。
#センター17本試物理基礎
水平面と角度 θ をなす、なめらかな斜面上の物体の運動を考える。重力加速度の大きさを g とする。
小物体を斜面上の点Pから斜面に沿って上向きに速さ v0 で打ち出したところ、図2のように小物体は斜面を上り、点Pから L だけ離れた点Qを速さ v で通過した。v を式で表わせ。
#センター17本試物理基礎
（解法1）
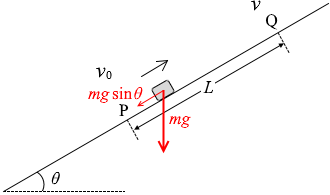小物体の運動する可能性のある方向は斜面方向であり、この方向にはたらく力は mgsinθ です。
小物体の加速度の大きさを a として運動方程式を立てますと、
ma = mgsinθ
∴ a = gsinθ
この値はずっと一定であるので、小物体の運動は等加速度直線運動（あるいは加速度の大きさが gsinθ の鉛直上方投射運動）ということになります。
等加速度直線運動（あるいは鉛直上方投射運動）の時間 t を含まない式を立てますと（右上方向を正とする）、
v2 - v02 = 2(-gsinθ)L
∴ v2 = v02 - 2gLsinθ
∴ v = \(\sqrt{{v_0}^2-2gL\sinθ}\)
（解法2）
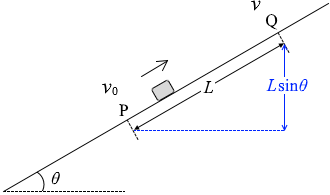
点Pを高さの基準面としますと、
点Pでの小物体の力学的エネルギーは
運動エネルギー：\(\large{\frac{1}{2}}\)mv02
位置エネルギー： 0
\(\large{\frac{1}{2}}\)mv02 + 0
点Qでの小物体の力学的エネルギーは
運動エネルギー：\(\large{\frac{1}{2}}\)mv2
位置エネルギー：mgLsinθ
\(\large{\frac{1}{2}}\)mv2 + mgLsinθ
力学的エネルギー保存の法則より、上の2式は等しいから、
\(\large{\frac{1}{2}}\)mv02 + 0 = \(\large{\frac{1}{2}}\)mv2 + mgLsinθ
∴ v02 = v2 + 2gLsinθ
∴ v2 = v02 - 2gLsinθ
∴ v = \(\sqrt{{v_0}^2-2gL\sinθ}\)
（『qHBF9』もご参照ください）