図1(a)のように、なめらかに動くピストンがついた断面積 S 、質量 M のシリンダーに 1mol の単原子分子理想気体を閉じ込め、シリンダーが鉛直に動くように、ピストンを天井に棒で固定した。気体はヒーターで温めることができる。ピストンとシリンダーは熱を通さず、それらの熱容量は無視できるものとする。最初、シリンダー内の気体の圧力は P 、温度は T 、体積は V であった。大気圧を P0 、気体定数を R 、重力加速度の大きさを g とする。
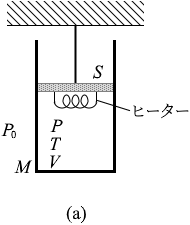
（問1）図1(a)の状態でシリンダーが静止しているとき、シリンダー内の気体の圧力 P を式で表わせ。
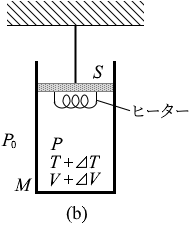
（問2）次に、シリンダー内の気体を温めると、シリンダーはゆっくりと下降し、図1(b)の状態でシリンダーは静止した。このときの温度は T + ⊿T であった。気体の内部エネルギーの増加分 ⊿U と、体積の増加分 ⊿V を表す式の組合せとして正しいものを、次の①～⑨のうちから一つ選べ。
| ⊿U | ⊿V | |
|---|---|---|
| ① | \(\large{\frac{1}{2}}\)R⊿T | \(\large{\frac{⊿T}{T}}\)V |
| ② | \(\large{\frac{1}{2}}\)R⊿T | \(\large{\frac{⊿T}{T+⊿T}}\)V |
| ③ | \(\large{\frac{1}{2}}\)R⊿T | \(\large{\frac{T}{T+⊿T}}\)V |
| ④ | R⊿T | \(\large{\frac{⊿T}{T}}\)V |
| ⑤ | R⊿T | \(\large{\frac{⊿T}{T+⊿T}}\)V |
| ⑥ | R⊿T | \(\large{\frac{T}{T+⊿T}}\)V |
| ⑦ | \(\large{\frac{3}{2}}\)R⊿T | \(\large{\frac{⊿T}{T}}\)V |
| ⑧ | \(\large{\frac{3}{2}}\)R⊿T | \(\large{\frac{⊿T}{T+⊿T}}\)V |
| ⑨ | \(\large{\frac{3}{2}}\)R⊿T | \(\large{\frac{T}{T+⊿T}}\)V |
（問3）図1(a)から(b)に変化する間に、ヒーターが気体に与えた熱量 Q を表す式として正しいものを、次の①～⑦のうちから一つ選べ。
① ⊿U + P⊿V ② ⊿U + P0⊿V ③ (P0 - P)⊿V ④ ⊿U - P⊿V ⑤ ⊿U - P0⊿V ⑥ P⊿U ⑦ ⊿U
#センター16追試物理
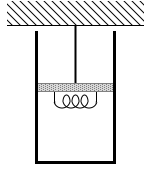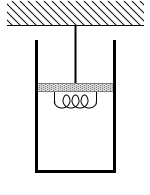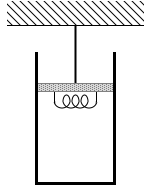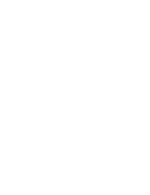この問題はピストンが固定されていてシリンダーが動くというものです。普通と逆です。
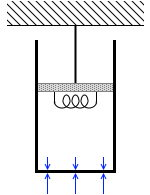内部の空気分子が押す力より外部の空気分子が押す力の方が強いのでシリンダーを支えることができるということです。
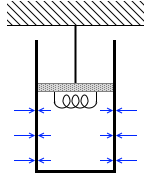このとき水平方向の力は考えません。シリンダーの鉛直方向の運動に無関係です。
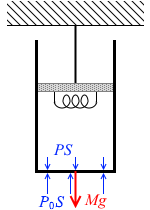シリンダーを内部の気体が押し下げる力は 
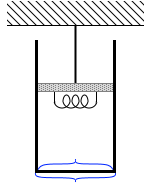問題文でシリンダーの厚みについて触れられておらず、厚みがあるとすると底面の大きさに違いが生じてしまいますが、
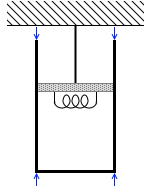下から押される分は上からも押され相殺されるので問題ありません。