(問1)
波の基本式 f = \(\large{\frac{1}{T}}\) に T = 3.0 を代入しますと、
f = \(\large{\frac{1}{3.0}}\)
波の基本式 v = fλ に v = 2.0 、f = \(\large{\frac{1}{3.0}}\) を代入しますと、
2.0 = \(\large{\frac{1}{3.0}}\) × λ
∴ λ = 6.0 [m]
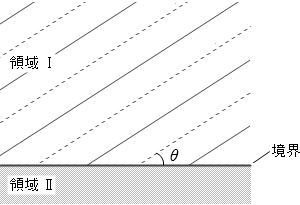
(問2)
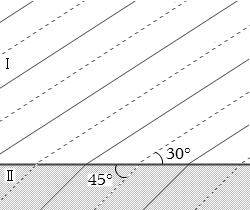
図2を分かりやすくするため、波を矢印に書き換えます。
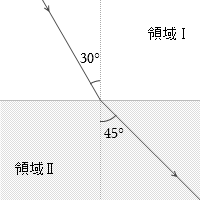
屈折の法則(スネルの法則)によれば、このときの
\(\large{\frac{\sin30°}{\sin45°}}\)
という比率は保たれます。
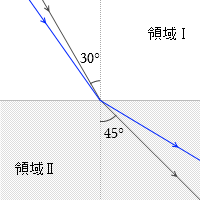
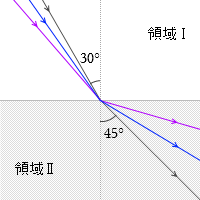
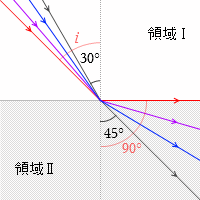
角度 θ を徐々に大きくしていく(黒線→青線→紫線→赤線)と、あるところ(赤線)で波は屈折しなくなり境界線上を進みます。これが初めて全反射した状態です。このときの入射角を臨界角といいます。この臨界角を求めよというのがこの問題の題意です。
初めて全反射が起こるときの屈折角というのは 90° です。そしてこのときも屈折の法則は生きていますから、臨界角を i と置くと、
\(\large{\frac{\sin30°}{\sin45°}}\) = \(\large{\frac{\sin i}{\sin90°}}\)
∴ \(\large{\frac{\frac{1}{2}}{\frac{1}{\sqrt{2}}}}\) = sini (∵ sin30°=\(\large{\frac{1}{2}}\)、sin45°=\(\large{\frac{1}{\sqrt{2}}}\)、sin90°=1)
∴ sini = \(\large{\frac{\frac{1}{2}\times\sqrt{2}}{\frac{1}{\sqrt{2}}\times\sqrt{2}}}\) = \(\large{\frac{1}{2}}\)×\(\sqrt{2}\) = \(\large{\frac{1}{\sqrt{2}}}\)
∴ i = 45°
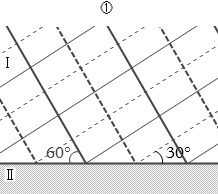
(問3)
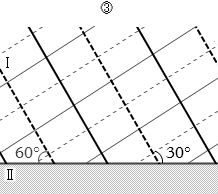
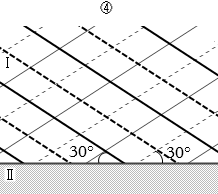
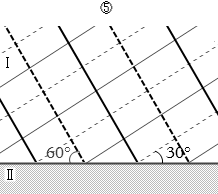
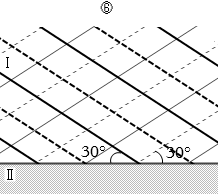
まず、反射の法則により、入射角と反射角は等しいので、反射角も 30° です。(屈折のときは角度が変わりますが、反射のときは角度は変わりません)。よって、②、④、⑥のいずれかです。
そして、固定端反射であるので、反射波の位相は π ズレます。位相が π ズレるというのは、入射したとき山だったものが反射するとき谷になるということです。
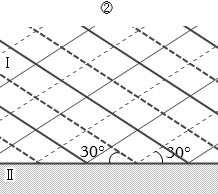
そのようになっているのは ⑥ です。
②は、境界において細実線が太実線に接していますので、入射波の山が反射して山となっているということであり、不適です。これは自由端反射です。
④は、境界において細線と太線がつながってないので固定端反射でも自由端反射でもなく、不適です。このような反射はありません。