(問1)
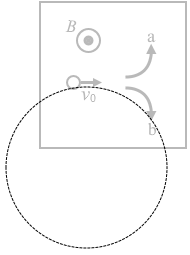
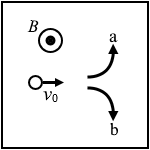
磁場中を進む荷電粒子はローレンツ力を受けますが、その大きさは
qv0B
であり、求める円運動の半径を r として円運動の運動方程式を立てますと、
m\(\large{\frac{{v_0}^2}{r}}\) = qv0B
∴ m\(\large{\frac{v_0}{r}}\) = qB
∴ r = \(\large{\frac{mv_0}{qB}}\)
また、周期を T と置きますと、
T = \(\large{\frac{2πr}{v_0}}\)
ω = \(\large{\frac{v}{r}}\) と
T = \(\large{\frac{2π}{ω}}\) より
T = \(\large{\frac{2πr}{v}}\)
= \(\large{\frac{2πm}{qB}}\)
回転の方向については、
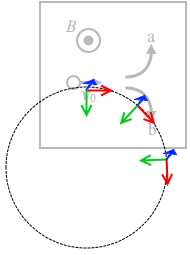 フレミングの左手の法則を適用しますと、 b 。
フレミングの左手の法則を適用しますと、 b 。
(問2)
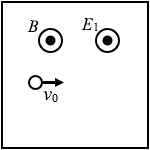 磁場に平行な電場が加わったということなので、電荷 q は紙面こちら向きに力を受けることになります。その力の大きさは
E = \(\large{\frac{F}{q}}\)
磁場に平行な電場が加わったということなので、電荷 q は紙面こちら向きに力を受けることになります。その力の大きさは
E = \(\large{\frac{F}{q}}\)
∴ F = qE
qE1
で、この力で電荷 q は紙面こちら向きに加速されるわけですが、その加速度の大きさは運動方程式(ma = F)の関係より、
\(\large{\frac{qE_1}{m}}\)
であり、t 秒後の紙面こちら向きの速さは
v = v0 + at
\(\large{\frac{qE_1}{m}}\)t
であり、
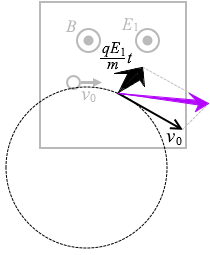 この速さを v0 と合成しますと(三平方の定理より)、
この速さを v0 と合成しますと(三平方の定理より)、
\(\sqrt{{v_0}^2+\big(\frac{qE_1}{m}t\big)^2}\)
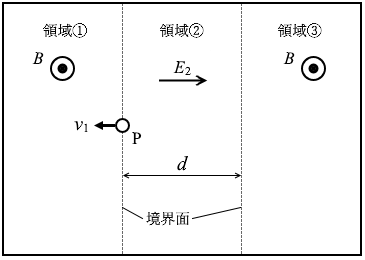
(問3)
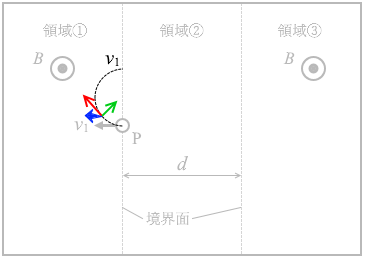 領域①の向きに打ち出された荷電粒子は右回りに円弧を描きます。(等速円運動)
領域①の向きに打ち出された荷電粒子は右回りに円弧を描きます。(等速円運動)
このときの荷電粒子の運動エネルギーは
\(\large{\frac{1}{2}}\)mv12
です。
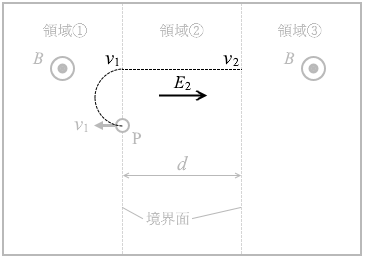 その後、領域②において荷電粒子は E2 によって加速されます。加速して領域③に到達した瞬間の速さを v2 と置きますと、そのときの運動エネルギーは
その後、領域②において荷電粒子は E2 によって加速されます。加速して領域③に到達した瞬間の速さを v2 と置きますと、そのときの運動エネルギーは
\(\large{\frac{1}{2}}\)mv22
ですが、
どのくらいエネルギーが増えたかといいますと、それは
qE2d
です。荷電粒子は領域②において qE2 の力を受けて、d だけ進みます。qE2 × d の仕事をされて、その分エネルギーが増えます(速さが増します)。これは『あらい水平面を進む物体』や『qG7FA』の逆のような話です。摩擦力を受けたときは減速して運動エネルギーが減りますが、本問の場合は、力を受けて加速し、運動エネルギーが増えます。
ですから、領域③に到達した瞬間の力学的エネルギーは
\(\large{\frac{1}{2}}\)mv22 = \(\large{\frac{1}{2}}\)mv12 + qE2d
となります。右辺が求める運動エネルギーの大きさです。(左辺は解答として不適です。自分で設定した v2 が含まれています。右辺は与えられた量のみで表現できています。)
そして、上式を解いて v2 を求めますと、
\(\large{\frac{1}{2}}\)mv22 = \(\large{\frac{1}{2}}\)mv12 + qE2d
∴ mv22 = mv12 + 2qE2d
∴ v22 = v12 + \(\large{\frac{2qE_2d}{m}}\)
∴ v2 = \(\sqrt{{v_1}^2+\large{\frac{2qE_2d}{m}}}\)
(問4)
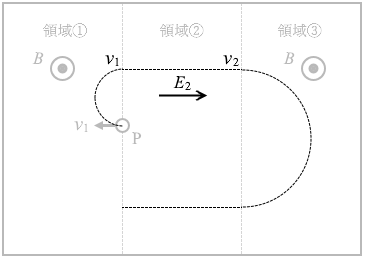 荷電粒子は領域①と③では円弧を描き、領域②では真っ直ぐ進むわけですが、問1を参考にしますと、
荷電粒子は領域①と③では円弧を描き、領域②では真っ直ぐ進むわけですが、問1を参考にしますと、
領域①での円の半径は
\(\large{\frac{mv_1}{qB}}\)
であり、領域③での円の半径は
\(\large{\frac{mv_2}{qB}}\)
であるので、点Pからの距離は
2×\(\large{\frac{mv_2}{qB}}\) - 2×\(\large{\frac{mv_1}{qB}}\) = \(\large{\frac{2m}{qB}}\)(v2 - v1)
= \(\large{\frac{2m}{qB}}\)\(\Bigg(\)\(\sqrt{{v_1}^2+\large{\frac{2qE_2d}{m}}}\) - \(v_1\)\(\Bigg)\)
(問5)
問1、問4で説明したように、円の半径は荷電粒子の速さに比例します。ですので、領域③での円運動の半径は領域①での半径の3倍になります。
また、領域③から領域①へ戻るとき、荷電粒子の速さは v1 に戻ります。領域②を進んでいる間、荷電粒子は qE2 の力を受け減速します。力学的エネルギー保存の式を立てると、
\(\large{\frac{1}{2}}\)mv12 = \(\large{\frac{1}{2}}\)mv22 - qE2d
となります。問3の式と同等です。①→③の過程では qE2d だけエネルギーが増え、③→①の過程では qE2d だけエネルギーが減ります。
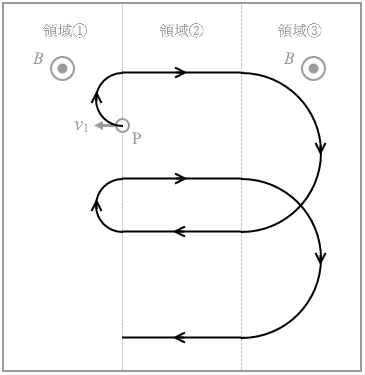
というわけで軌跡の図は以下のようになります。


 磁場に平行な電場が加わったということなので、電荷 q は紙面こちら向きに力を受けることになります。その
磁場に平行な電場が加わったということなので、電荷 q は紙面こちら向きに力を受けることになります。その この速さを v0 と合成しますと(三平方の定理より)、
この速さを v0 と合成しますと(三平方の定理より)、 領域①の向きに打ち出された荷電粒子は右回りに円弧を描きます。(等速円運動)
領域①の向きに打ち出された荷電粒子は右回りに円弧を描きます。(等速円運動) その後、領域②において荷電粒子は E2 によって加速されます。加速して領域③に到達した瞬間の速さを v2 と置きますと、そのときの運動エネルギーは
その後、領域②において荷電粒子は E2 によって加速されます。加速して領域③に到達した瞬間の速さを v2 と置きますと、そのときの運動エネルギーは 荷電粒子は領域①と③では円弧を描き、領域②では真っ直ぐ進むわけですが、問1を参考にしますと、
荷電粒子は領域①と③では円弧を描き、領域②では真っ直ぐ進むわけですが、問1を参考にしますと、