(問1)M ⋅0 + (- mu )
衝突後の運動量の和: (- M v A ) + m v B
運動量保存の法則 より、
M ⋅0 + (- mu ) = (- M v A ) + m v B
∴ - mu = - M v A + m v B
∴ m v B = M v A - mu
∴ v B = \(\large{\frac{M}{m}}\)v A - u ……①
また、弾性衝突(e = 1)であることから反発係数の式 (e = \(-\large{\frac{v_1{'}-v_2{'}}{v_1-v_2}}\))に各量を代入して v A を求めますと、
1 = \(-\large{\frac{-(v_\rm{A})-v_\rm{B}}{0-(-u)}}\)
∴ 1 = \(\large{\frac{v_\rm{A}+v_\rm{B}}{u}}\)
∴ u = v A + v B ①式を代入して
∴ u = v A + \(\large{\frac{M}{m}}\)v A - u
∴ 2u = (1 + \(\large{\frac{M}{m}}\))v A
∴ 2u = \(\large{\frac{m+M}{m}}\)v A
∴ 2u \(\large{\frac{m}{m+M}}\) = v A
∴ v A = \(\large{\frac{2m}{M+m}}\)u
これを①式に代入しますと、
v B = \(\large{\frac{M}{m}}\)v A - u
= \(\large{\frac{M}{m}}\)⋅\(\large{\frac{2m}{M+m}}\)u - u
= \(\large{\frac{2M}{M+m}}\)u - u
= \(\large{\frac{2M-(M+m)}{M+m}}\)u
= \(\large{\frac{M-m}{M+m}}\)u
v B は速度でなく速さを表す量であり、M > m であるので、上式を読み取るとちゃんと正になってます。ここが負になっていると何かしら間違っているということです。
(問2)単なる単振り子 ではなく微小振動の単振り子であるということであり、微小振動の単振り子の周期 の公式( T = 2π \(\sqrt{\frac{\large{l}}{\large{g}}}\) )が使えるということです。
求める周期を T と置きますと、
T = 2π \(\sqrt{\frac{\large{l}}{\large{g}}}\)
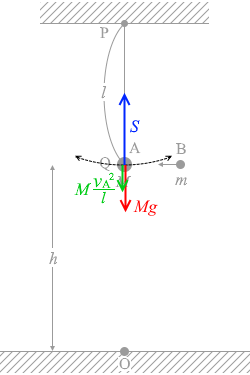
求める張力を S と置きますと、
Mg で、
遠心力 が \(M\large{\frac{{v_\rm{A}}^2}{l}}\) で、
これらが張力とつり合っているので、
S = Mg + \(M\large{\frac{{v_\rm{A}}^2}{l}}\) *
あるいは、円運動の運動方程式 として、S - Mg 閉じる
= \(M(g +\large{\frac{{v_\rm{A}}^2}{l}}\normalsize{)}\)
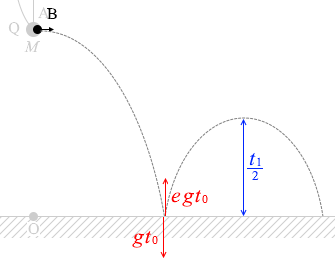
(問3)水平投射の鉛直方向の位置の式 (y = \(\large{\frac{1}{2}}\)gt 2 )に各量を代入しますと、
h = \(\large{\frac{1}{2}}\)gt 0 2
∴ \(\large{\frac{2h}{g}}\) = t 0 2
∴ t 0 = \(\sqrt{\frac{\large{2h}}{\large{g}}}\)
(問4)
(床への衝突直前の速度の鉛直成分の大きさ)g の加速度で t 0 の時間進むわけですから、床への衝突直前の速度の鉛直成分の大きさは
gt 0
(床への衝突直後の速度の鉛直成分の大きさ)反発係数 e で跳ね返る (e = \(\large{\frac{|v'|}{|v|}}\))のですから、床への衝突直後の速度の鉛直成分の大きさは
egt 0
この速さが g の加速度で \(\large{\frac{t_1}{2}}\) の時間だけ経つと(最高点で) 0 になるのだから、
egt 0 = \(g\large{\frac{t_1}{2}}\) ……②
∴ et 0 = \(\large{\frac{t_1}{2}}\)
∴ t 1 = 2et 0
問3の t 0 の値を代入して
t 1 = 2e \(\sqrt{\frac{\large{2h}}{\large{g}}}\)
(問5)
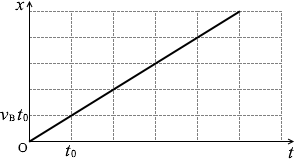
(水平方向)*
『水平投射 』項参照
閉じる x = v B t となります。
(鉛直方向)h 1 として、鉛直上方投射のt を含まない式 (v 2 - v 0 2 = - 2gy )を立てますと、
02 - (egt 0 )2 = - 2gh 1
∴ - e 2 g 2 t 0 2 = - 2gh 1
∴ e 2 g t 0 2 = 2h 1 問3で求めた t 0 = \(\sqrt{\frac{\large{2h}}{\large{g}}}\) を代入して
∴ e 2 g \(\frac{\large{2h}}{\large{g}}\) = 2h 1
∴ e 2 2h = 2h 1
∴ h 1 = e 2 h
さらに、床への2回目の衝突直後の速度の鉛直成分の大きさは(問4と同様に考えて)
e ×egt 0 = e 2 gt 0
であり、床に2回目に衝突した後の最高点の高さを h 2 としますと、(上記と同様の式を立てて)
02 - (e 2 gt 0 )2 = - 2gh 2
∴ e 4 g t 0 2 = 2h 2 t 0 = \(\sqrt{\frac{\large{2h}}{\large{g}}}\) を代入して
∴ e 4 g \(\frac{\large{2h}}{\large{g}}\) = 2h 2
∴ h 2 = e 4 h
さらに、h 3 と置いて同様に計算すると、
02 - (e 3 gt 0 )2 = - 2gh 3
∴ h 3 = e 6 h
また、床に2回目に衝突してから3回目に衝突するまでの時間を t 2 として問4の②式と同様の式を立てると、
e 2 gt 0 = \(g\large{\frac{t_2}{2}}\)
∴ e 2 t 0 = \(\large{\frac{t_2}{2}}\)
∴ t 2 = 2e 2 t 0
さらに、t 3 と置いて計算すると、
e 3 gt 0 = \(g\large{\frac{t_3}{2}}\)
∴ t 3 = 2e 3 t 0
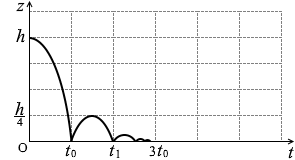
以上まとめますと、
高さはh h 1 = e 2 h h 2 = e 4 h h 3 = e 6 h …
時間は(t 0 だけ定義がちょっと違いますが)t 0 t 1 = 2et 0 t 2 = 2e 2 t 0 t 3 = 2e 3 t 0 …
となります。
題意より e = 0.5 であるので、跳ね返るごとに高さは \(\large{\frac{1}{4}}\) になり、時間は \(\large{\frac{1}{2}}\) になる、ということです。つまりグラフは以下のようになります。
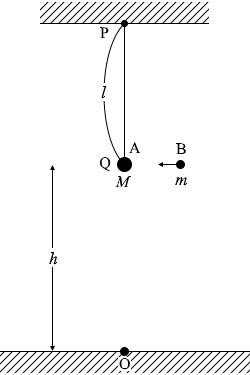
 重力が Mg で、
重力が Mg で、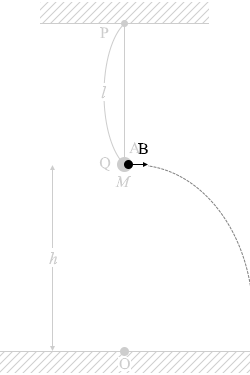 衝突後、小球Bは水平投射運動をします。
衝突後、小球Bは水平投射運動をします。