電磁波の発生
変位電流
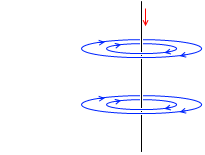導線に電流が流れると周りに磁場が発生しますが、
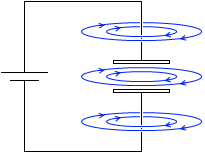コンデンサーと電池をつないだ回路においては、導線の周りだけでなく極板の間の部分にも磁場が発生します。導線の周りに発生したのと同じ大きさの磁場が極板の間にも発生します。
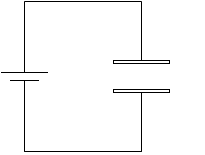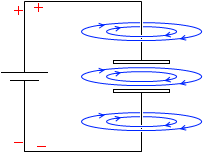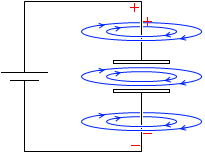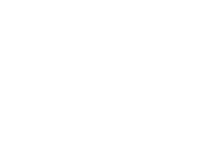しかし、コンデンサーが満充電になると電流は流れなくなるので、磁場は消えてしまいます。
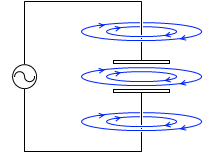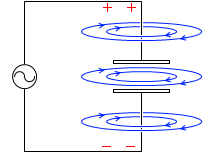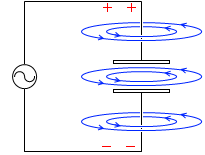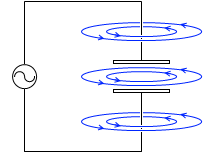磁場を発生させ続けるには電池（直流電源）ではなく交流電源を用いる必要があります。交流電源を用いれば電流は流れ続け、磁場も発生し続けます。（『振動回路』項参照）。このとき電流の向きは刻々と変わります。それに伴って磁場の向きも刻々と変わります。
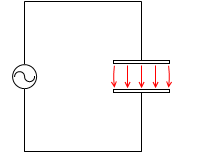このときコンデンサーの極板間の電場の変化を架空の電流とみなし、変位電流＊「変位電流」は、考え方も抽象的ですが、ネーミングも抽象的です。名前が付けられた経緯は分かりません。
閉じるあるいは電束電流と呼びます。
電場と磁場
このことは、電荷が実際に移動してなくても、電場が変化していればその周りに磁場が発生するということを意味しています。
また、電磁誘導というものは磁場が変化すると誘導起電力が発生するというものでしたが、これは言い換えれば、磁場が変化すると電場が発生するということです。
この２つの原理により、電場と磁場が次々に発生することになります。
三角関数の微分は三角関数
もし、電場の変化の仕方が単振動であった場合、それに伴って発生する磁場の変化も単振動になり、さらにその磁場の変化によって発生する電場の変化も単振動になります。電磁誘導の法則の式 V = - N\(\large{\frac{ΔΦ}{Δt}}\) は磁場を微分したものが電場になることを表しており、磁場の変化が単振動、つまり三角関数であればそれを微分しても三角関数であるので、磁場が作る電場も三角関数、その電場が作る磁場も三角関数、さらにその電場が作る磁場も三角関数となり、次々に電場と磁場が作られていきます。
たとえば、sinx を微分すると cosx で、これをさらに微分すると -sinx で、これをさらに微分すると -cosx で…、と永遠に三角関数になります。
グラフで表すと、
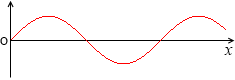sinx、
これを微分すると、
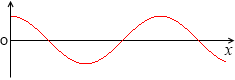cosx であり、上の sinx の曲線を横にずらしただけのものです。
さらに、これを微分すると、
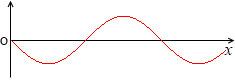-sinx であり、sinx の曲線を反転させただけのものです。
さらに、これを微分すると、
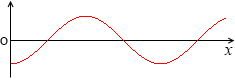-cosx であり、sinx の曲線を横にずらして反転させただけのものです。
このように正弦曲線は微分しても正弦曲線になります＊不正確な言い方ですが…。閉じる。
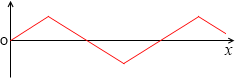他方、三角波、たとえば 2x、-2x 、2x 、…
これを微分すると、
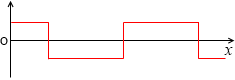2 、-2 、2 、…
さらに、これを微分すると、
0 。
というふうに、続かなくなってしまいます。
三角関数であれば永遠に続きます。
電磁波
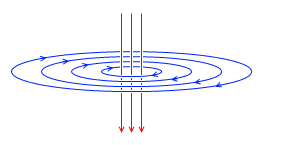電場の強さの変化はあらゆる地点に影響を及ぼし、
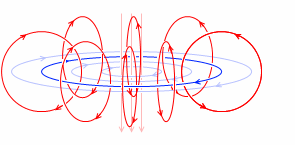それによって作られる磁場もあらゆる地点に影響を及ぼし、
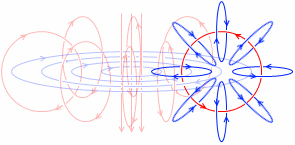さらにそれによって作られる電場もあらゆる地点に影響を及ぼし…と、次々に作用し合いますが、ホイヘンスの原理により、強め合った成分だけが残り、それが波として伝わっていきます。この波を電磁波といいます。
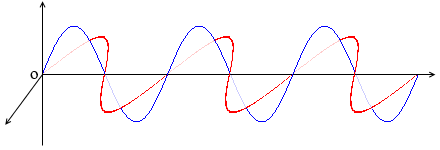ある一つの直線上の電磁波を観察すると左図のような波になっています。＊このようなきれいな正弦波であるとは限りませんが、少なくとも大小の三角関数の波形を組み合わせた形になっています。
閉じる
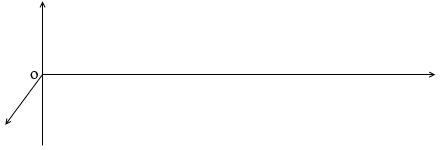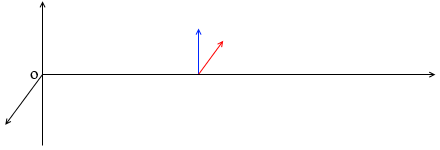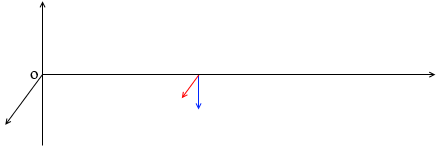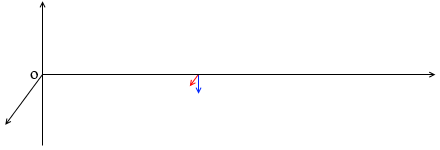これは、各地点の電場と磁場が単振動の変化の仕方＊あるいは大小の単振動を組み合わせた変化の仕方
閉じるをしているという意味です。
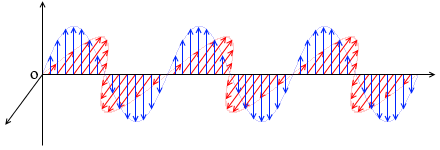各地点の電場と磁場の変化の様子を連ねると波の形になるということです。
アンテナ
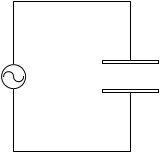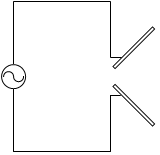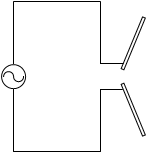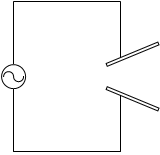コンデンサーの極板の形を変えれば、電磁波が放射される方向や、電磁波の波長を変えることができます＊波長に関しては共振周波数を変えることによって調整できるのではありますが、アンテナの長さを狙いの波長の 1/4 や 1/2 にしたりすると、より安定的に狙い通りの波長の電磁波を送受信できるようになります。
電磁波の振幅の大きさは波の強さを表していて、例えば、発信機を 100V の電源に繋いだときより 200V の電源に繋いだときの方が、振幅は大きくなります。それだけのことです。ですから、電磁波においては振幅の大きさよりも波長の大きさが重要要素となります。
閉じる。コンデンサーの極板を変形したものがアンテナです。形状を工夫することによって狙い通りの方角や狙い通りの波長の電磁波を送受信することができます。