振動回路
コンデンサーとコイルだけを接続した回路
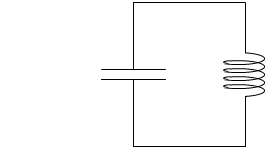 コンデンサーとコイルだけを接続した単純な回路に、どのような電流が流れるか考えてみます。
コンデンサーとコイルだけを接続した単純な回路に、どのような電流が流れるか考えてみます。
といってもこれではコンデンサーが充電できないので、下図のような回路について考えます。
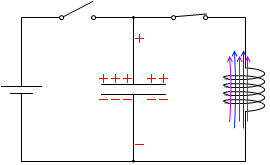
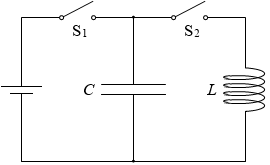 左図のように、電気容量 C [F] のコンデンサー、自己インダクタンス L [H] のコイル、スイッチS1、S2 を電池に接続します。
左図のように、電気容量 C [F] のコンデンサー、自己インダクタンス L [H] のコイル、スイッチS1、S2 を電池に接続します。
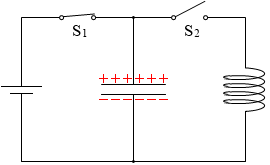 始めに、S1 を閉じてコンデンサーを充電します。フルに充電します。
始めに、S1 を閉じてコンデンサーを充電します。フルに充電します。
電池が作る電流は交流ではなく直流ですから、この時点で流れた電流は直流です。
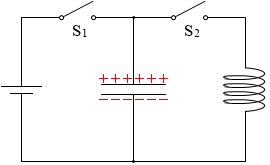 次に、S1 を開きます。
次に、S1 を開きます。
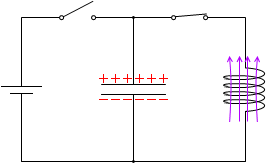 t=0:次に、S2 を閉じます。するとコンデンサーに貯まっていた電荷が移動します(放電)。このときコイルに電流が流れることになるわけですが、コイルに電流が流れ、その大きさが変化するということは、自己誘導起電力が発生し、それが電流の増減の変化を邪魔するということです。
t=0:次に、S2 を閉じます。するとコンデンサーに貯まっていた電荷が移動します(放電)。このときコイルに電流が流れることになるわけですが、コイルに電流が流れ、その大きさが変化するということは、自己誘導起電力が発生し、それが電流の増減の変化を邪魔するということです。
閉じた瞬間は電流が急激に(極板の電荷がまるで大海原に飛び出していくように)増えるので自己誘導起電力が大きくなります。
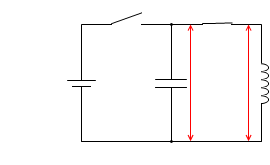 自己誘導起電力というのはコイルに発生する起電力ですが、キルヒホッフ第2法則により、コンデンサーとコイルに掛かる電圧は等しいので、同じ大きさの電圧がコンデンサーにも掛かります。
自己誘導起電力というのはコイルに発生する起電力ですが、キルヒホッフ第2法則により、コンデンサーとコイルに掛かる電圧は等しいので、同じ大きさの電圧がコンデンサーにも掛かります。
つまり S2 を閉じた瞬間というのは、電流が 0 から急激に増えていくとともに、電圧がもっとも大きくなっています。
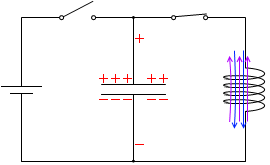 t=\(\large{\frac{1}{16}}\)T:左図において右回りを正としますと、正電荷は右回りに移動していきますので、このとき流れる電流は正ということになります。*
t=\(\large{\frac{1}{16}}\)T:左図において右回りを正としますと、正電荷は右回りに移動していきますので、このとき流れる電流は正ということになります。*
『正電荷』項で説明したことですが、
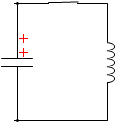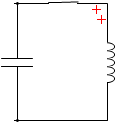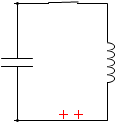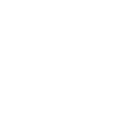 正電荷が右回りに動くことと、
正電荷が右回りに動くことと、
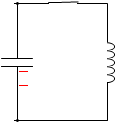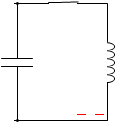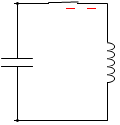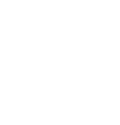 負電荷が左回りに動くことは同じことです。
負電荷が左回りに動くことは同じことです。
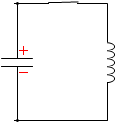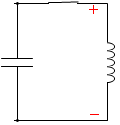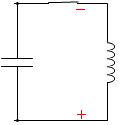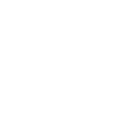 さらにいうと、このような動きも同じことです。
さらにいうと、このような動きも同じことです。
これら3つは共に、電流が右回りに流れたことを表しています。
閉じる
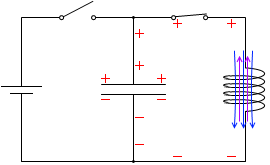 t=\(\large{\frac{2}{16}}\)T:電流の増加の程度は徐々に落ち着いていき、
t=\(\large{\frac{2}{16}}\)T:電流の増加の程度は徐々に落ち着いていき、
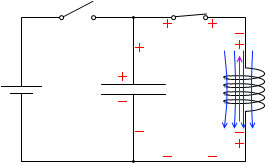 t=\(\large{\frac{3}{16}}\)T:自己誘導起電力は小さくなっていきます。
t=\(\large{\frac{3}{16}}\)T:自己誘導起電力は小さくなっていきます。
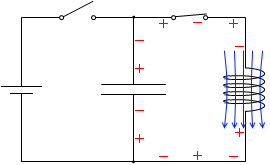 t=\(\large{\frac{4}{16}}\)T:電荷が均等に分布したときが、電流が最大となります。このとき電流の変化は一瞬止みますので、自己誘導起電力は 0 になります。
t=\(\large{\frac{4}{16}}\)T:電荷が均等に分布したときが、電流が最大となります。このとき電流の変化は一瞬止みますので、自己誘導起電力は 0 になります。
自己誘導起電力は 0 になりますが、電荷は(振り子のように)そのままの勢いで進んでいき、
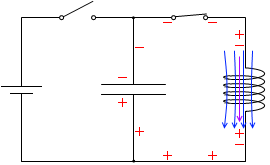 t=\(\large{\frac{5}{16}}\)T:電荷が極板に貯まり始め、つまり電流が減り始めると、今度は電流を増やそうとする向きに自己誘導起電力が発生します。
t=\(\large{\frac{5}{16}}\)T:電荷が極板に貯まり始め、つまり電流が減り始めると、今度は電流を増やそうとする向きに自己誘導起電力が発生します。
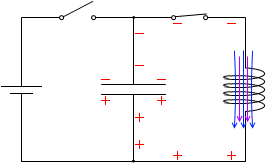 t=\(\large{\frac{6}{16}}\)T:電流の減少の程度は徐々に増していき、
t=\(\large{\frac{6}{16}}\)T:電流の減少の程度は徐々に増していき、
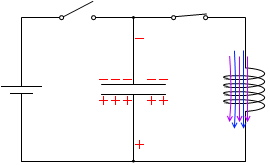 t=\(\large{\frac{7}{16}}\)T:自己誘導起電力は大きくなっていきます。
t=\(\large{\frac{7}{16}}\)T:自己誘導起電力は大きくなっていきます。
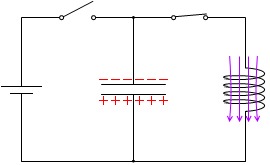 t=\(\large{\frac{8}{16}}\)T:もっとも電流の減少量が大きいときに電流の大きさは 0 になり、このとき自己誘導起電力は最大となり、その向きは t=0 のときと逆です。コンデンサーの極板の電荷の正負も t=0 のときと逆になっています。
t=\(\large{\frac{8}{16}}\)T:もっとも電流の減少量が大きいときに電流の大きさは 0 になり、このとき自己誘導起電力は最大となり、その向きは t=0 のときと逆です。コンデンサーの極板の電荷の正負も t=0 のときと逆になっています。
極板に貯まった電荷は押し合いへし合いをし、
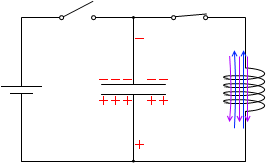 t=\(\large{\frac{9}{16}}\)T:再び放電が始まり、電流がこれまでとは逆向きに流れ始めます。(まるで大海原に飛び出す電荷たちによって)電流の大きさは急激に増えます(向きは負)。
t=\(\large{\frac{9}{16}}\)T:再び放電が始まり、電流がこれまでとは逆向きに流れ始めます。(まるで大海原に飛び出す電荷たちによって)電流の大きさは急激に増えます(向きは負)。
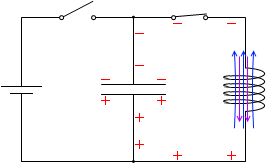 t=\(\large{\frac{10}{16}}\)T:電流の変化は徐々に落ち着いていき、
t=\(\large{\frac{10}{16}}\)T:電流の変化は徐々に落ち着いていき、
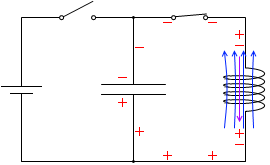 t=\(\large{\frac{11}{16}}\)T:自己誘導起電力の大きさは小さくなっていきます。
t=\(\large{\frac{11}{16}}\)T:自己誘導起電力の大きさは小さくなっていきます。
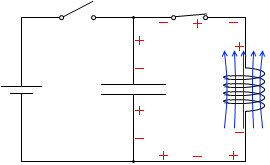 t=\(\large{\frac{12}{16}}\)T:負の電流の大きさが最大になった瞬間は、変化量が 0 で、自己誘導起電力が 0 になります。
t=\(\large{\frac{12}{16}}\)T:負の電流の大きさが最大になった瞬間は、変化量が 0 で、自己誘導起電力が 0 になります。
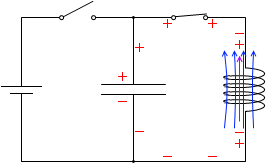 t=\(\large{\frac{13}{16}}\)T:負の電流の大きさが小さくなり始めると、今度は電流を増やそうとする向きに自己誘導起電力が発生します。
t=\(\large{\frac{13}{16}}\)T:負の電流の大きさが小さくなり始めると、今度は電流を増やそうとする向きに自己誘導起電力が発生します。
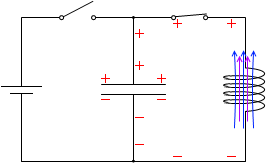 t=\(\large{\frac{14}{16}}\)T:電流の変化量は徐々に大きくなり、
t=\(\large{\frac{14}{16}}\)T:電流の変化量は徐々に大きくなり、
 t=\(\large{\frac{15}{16}}\)T:自己誘導起電力の大きさが大きくなっていきます。
t=\(\large{\frac{15}{16}}\)T:自己誘導起電力の大きさが大きくなっていきます。
 t=T=0:もっとも電流の変化量が大きいときに電流の大きさは 0 になり、このとき自己誘導起電力は最大となり、これはつまり t=0 の状態と同じになります。
t=T=0:もっとも電流の変化量が大きいときに電流の大きさは 0 になり、このとき自己誘導起電力は最大となり、これはつまり t=0 の状態と同じになります。
ここまでの動作を繰り返し、結局この回路には交流電流が流れることになります。交流電源を用いていないのに交流が流れるのです。
グラフ
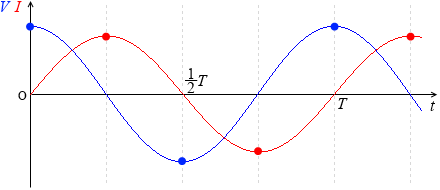
 振動回路の電流と電圧のグラフを描いてみます。電流は左図において右回りを正とします。電圧はコンデンサーに掛かる電圧とし、左図において極板の上側が正に帯電しているときを正とします。
振動回路の電流と電圧のグラフを描いてみます。電流は左図において右回りを正とします。電圧はコンデンサーに掛かる電圧とし、左図において極板の上側が正に帯電しているときを正とします。
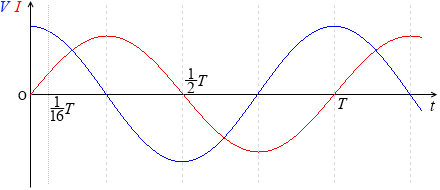 S2スイッチを閉じる前は、極板に電荷が目一杯貯まっていて、コンデンサーの電圧も最大になっていて、しかし電流はまだ流れておらず、スイッチを閉じた瞬間、極板の電荷たちが勢い良く飛び出し、電流が増えていき、電圧は小さくなっていきます。
S2スイッチを閉じる前は、極板に電荷が目一杯貯まっていて、コンデンサーの電圧も最大になっていて、しかし電流はまだ流れておらず、スイッチを閉じた瞬間、極板の電荷たちが勢い良く飛び出し、電流が増えていき、電圧は小さくなっていきます。
最初の状態に戻る瞬間までが、1周期(=T)であるといえます。
式
 コンデンサーの電気量を Q [C] 、コンデンサーの電位差を V [V] としますと、いま電気容量を C [F] としていますので、
コンデンサーの電気量を Q [C] 、コンデンサーの電位差を V [V] としますと、いま電気容量を C [F] としていますので、
Q = CV です。
コイルに掛かる電圧の大きさは上で説明したようにコンデンサーに掛かる電圧と等しいです、ただし向きが逆なので -V です。そしていま自己インダクタンスを L [H] としていますので、
-V = - L\(\large{\frac{ΔI}{Δt}}\) つまり、
V = L\(\large{\frac{ΔI}{Δt}}\) です。
コイルの電流を I [A] とします。電流というのは、I = \(\large{\frac{ΔQ}{Δt}}\) という関係がありますが、今、コンデンサーの電気量 Q が減っていく局面で、コイルに正の電流が流れるので、正負を厳密に考えると、
I = - \(\large{\frac{ΔQ}{Δt}}\) です。
これらの式を微分の形で書き直します。
Q = CV ……①
V = L\(\large{\frac{ΔI}{Δt}}\) ……②
I = - \(\large{\frac{ΔQ}{Δt}}\) ……③
①式を V = \(\large{\frac{Q}{C}}\) と変形して②式の左辺に代入しますと、
\(\large{\frac{Q}{C}}\) = L\(\large{\frac{dI}{dt}}\)
この式の右辺に③式を代入しますと、
\(\large{\frac{Q}{C}}\) = - L\(\large{\frac{d^2Q}{dt^2}}\)
(これは大学物理の範囲なので申し訳ないのですが)上の式は単振動の微分方程式の形になっています。Q の増減の仕方は単振動の動きになります。上式を変形すると、
\(\large{\frac{d^2Q}{dt^2}}\) = - \(\large{\frac{Q}{LC}}\)
となりますが、
\(\large{\frac{d^2x}{dt^2}}\) = - ●x
という形の式において x は単振動と同じ変化の仕方をします。たとえばバネの動きは単振動になりますが、その弾性力を表す式は、
F = - k x
であり、F = ma を代入すると、
ma = - k x
であり、さらに、a = \(\large{\frac{d^2x}{dt^2}}\) を代入すると、
m\(\large{\frac{d^2x}{dt^2}}\) = - k x
であり、
\(\large{\frac{d^2x}{dt^2}}\) = - \(\large{\frac{k}{m}}\) x
となり、このような形の式の x は単振動の動きになります。
単振動ということは、その変位は x = Asinωt で表されます。(丁寧にいえば x = Asin(ωt+φ) です)
*
変化の仕方が単振動になる、ということは横軸を時間にとったグラフを描くと、
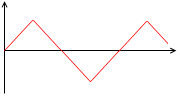 このような三角波になるのではなく、
このような三角波になるのではなく、
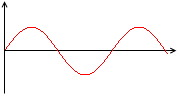 このような正弦波(正弦曲線)になる、ということです。
このような正弦波(正弦曲線)になる、ということです。
閉じる
\(\large{\frac{d^2Q}{dt^2}}\) = - \(\large{\frac{Q}{LC}}\) ……④
という式においては、
Q = Q0sin(ωt+\(\large{\frac{\pi}{2}}\)) (Q0は最大値。*
sinωt と置いてしまっても結果は同じですし間違いではないのですが、
本項の上の方の説明において t=0 のときに Q が最大、というイラストを描きましたので、
sin(ωt+\(\large{\frac{\pi}{2}}\)) としました。
これですと t=0 のときにちゃんと Q = Q0 となります。
sinωt と置いてしまうと、t=0 のときに Q = 0 となってしまいます。
なお、sinωt も cosωt も sin(ωt+\(\large{\frac{\pi}{2}}\)) もそのグラフは横にズラしただけの関係にあり、本質的には同じものです。
閉じる)
と置くことができ、変形しますと、
Q = Q0cosωt ( sin(ωt+\(\large{\frac{\pi}{2}}\)) = cosωt ) ……⑤
これを t で微分しますと、
\(\large{\frac{dQ}{dt}}\) = - Q0ωsinωt (cosAx の微分は -AsinAx) ……⑥
さらにもう一回 t で微分しますと、
\(\large{\frac{d^2Q}{dt^2}}\) = - Q0ω2cosωt (sinAx の微分は AcosAx) ……⑦
④式の左辺に⑦式を、右辺に⑤式を代入しますと、
- Q0ω2cosωt = - \(\large{\frac{1}{LC}}\)Q0cosωt
この式より、
ω2 = \(\large{\frac{1}{LC}}\) ……⑧
∴ ω = \(\large{\frac{1}{\sqrt{LC}}}\)
これは『共振回路』項の共振角周波数の値と同じであり、f = \(\large{\frac{ω}{2π}}\) に代入すると f = \(\large{\frac{1}{2π\sqrt{LC}}}\) であり、『共振回路』項の共振周波数と同じになります。
この周波数のことを固有周波数(固有振動数)といい、固有周波数で振動する回路を振動回路といい、この振動のことを電気振動といいます。
固有周波数
f = \(\large{\frac{1}{2π\sqrt{LC}}}\)
整理
『共振回路』項と本項の話を整理しますと、
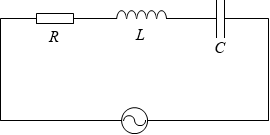 R と L と C と交流電源を直列に接続した回路では、いろいろと変えられる電源の周波数の中で f0 = \(\large{\frac{1}{2π\sqrt{LC}}}\) という大きさの周波数のときに電流が一番大きくなり、
R と L と C と交流電源を直列に接続した回路では、いろいろと変えられる電源の周波数の中で f0 = \(\large{\frac{1}{2π\sqrt{LC}}}\) という大きさの周波数のときに電流が一番大きくなり、
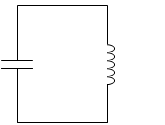
 C と L だけを接続した回路では、
C と L だけを接続した回路では、
電流が自然と f = \(\large{\frac{1}{2π\sqrt{LC}}}\) という周波数の交流になる、
となります。
固有振動
固有周波数は L と C の値によって決まるわけですが、これはつまりコンデンサーとコイルの形状等によって決まるということであり、それぞれの回路固有の値ということです。このことは、弦の振動や気柱の振動の電気版と見ることができます。また『共振回路』項の共振は『共振・共鳴』項の電気版ということがいえます。
減衰振動
 理想的な(仮想的な)振動回路では、抵抗が無いと考えるため、
理想的な(仮想的な)振動回路では、抵抗が無いと考えるため、
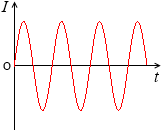 電流-時間グラフは左図のようになりますが、
電流-時間グラフは左図のようになりますが、
 実際の回路には抵抗がありますので、電流は時間と共に弱まっていき、*
抵抗の他に電磁波の放出という要因でも電流は弱まっていきます。
実際の回路には抵抗がありますので、電流は時間と共に弱まっていき、*
抵抗の他に電磁波の放出という要因でも電流は弱まっていきます。
電磁波の放出によってエネルギーが減少していきます。
抵抗に比べればはるかに小さい要因ですが。
閉じる
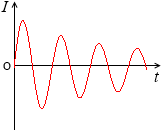 電流-時間グラフは左図のようになります。
電流-時間グラフは左図のようになります。
このような振動を減衰振動といいます。バネの振動が徐々に弱まっていくのと同じです。
エネルギー
振動回路においてエネルギーがどうなっているか考えてみます。
(i) コンデンサーに蓄えられるエネルギーの式
UC = \(\large{\frac{1}{2}}\)QV = \(\large{\frac{1}{2}}\)CV2 = \(\large{\frac{Q^2}{2C}}\)
の Q の部分に上で示した⑤式 Q = Q0cosωt を代入しますと、
UC = \(\large{\frac{Q^2}{2C}}\) = \(\large{\frac{(Q_0\cosωt)^2}{2C}}\) = \(\large{\frac{Q_0^2}{2C}}\)cos2ωt
(ii) 一方、コイルに蓄えられるエネルギーの式
UL = \(\large{\frac{1}{2}}\)LI2
の I の部分に上で示した⑥式 I = \(\large{\frac{dQ}{dt}}\) = - Q0ωsinωt を代入しますと、
UL = \(\large{\frac{1}{2}}\)L(-Q0ωsinωt)2 = \(\large{\frac{1}{2}}\)LQ02ω2sin2ωt
さらに、ω2 の部分に⑧式 ω2 = \(\large{\frac{1}{LC}}\) を代入しますと、
UL = \(\large{\frac{1}{2}}\)LQ02\(\large{\frac{1}{LC}}\)sin2ωt = \(\large{\frac{Q_0^2}{2C}}\)sin2ωt
(i) と (ii) を足しますと、
U = \(\large{\frac{Q_0^2}{2C}}\)cos2ωt + \(\large{\frac{Q_0^2}{2C}}\)sin2ωt
= \(\large{\frac{Q_0^2}{2C}}\)(sin2ωt + cos2ωt) (sin2x + cos2x = 1 ですから)
= \(\large{\frac{Q_0^2}{2C}}\)
となりまして、t の文字が消えます。時間に依らないということです。Q0 は最大値のことです。定数です。つまり、この回路の全体のエネルギーは時間によって変化しない、一定である、ということです。これはエネルギーが保存されていることを意味します。(あくまでも抵抗の無い理想的な振動回路での話です。現実的には抵抗によって多少なりともジュール熱が発生し、エネルギーは減っていきます)。
UC と UL を合わせたものは一定ですが、個々の UC と UL は時間によって変化します。
UC = \(\large{\frac{Q^2}{2C}}\) が最大のときというのはコンデンサーの電圧 V が、
 最大のとき(t=0)や、
最大のとき(t=0)や、
 最小のとき(t=\(\large{\frac{8}{16}}\)T)です。
最小のとき(t=\(\large{\frac{8}{16}}\)T)です。
極板に電荷がたくさん溜まっている瞬間です。
UL = \(\large{\frac{1}{2}}\)LI2 が最大のときというのは電流 I が、
 最大のとき(t=\(\large{\frac{4}{16}}\)T)や、
最大のとき(t=\(\large{\frac{4}{16}}\)T)や、
 最小のとき(t=\(\large{\frac{12}{16}}\)T)です。
最小のとき(t=\(\large{\frac{12}{16}}\)T)です。
UC 、UL の片方が最大のときは、もう片方が 0 になっています。
ばね振り子のエネルギーと同じ
この関係はばね振り子のエネルギーの関係と同じです。(『力学的エネルギー保存の法則』項、『ばね振り子』項、『単振り子』項もご参照ください)。トータルでの力学的エネルギーは一定で、個々の運動エネルギーと弾性エネルギーは時間によって変化し、片方が最大のときもう片方は 0 です。
U電気 = \(\large{\frac{1}{2}}\)\(\large{\frac{Q^2}{C}}\)+\(\large{\frac{1}{2}}\)LI2
U力学 = \(\large{\frac{1}{2}}\)kx2 + \(\large{\frac{1}{2}}\)mv2
 これらのことからしますと、らせん状の金属というものは電気的にも力学的にもその性質が似ているといえます。これは偶然のようであり、必然のようでもあります。
これらのことからしますと、らせん状の金属というものは電気的にも力学的にもその性質が似ているといえます。これは偶然のようであり、必然のようでもあります。
 と表したり
と表したり  と表したりします。
と表したりします。